728x90
1. 수요예측 기법 및 예측오차
- Forecasting : 모든 decision의 중요 input이 된다
- Forecasting이 필요한 이유
- Forecasting을 기본으로 해서 결정되는 것들이 너무 많음
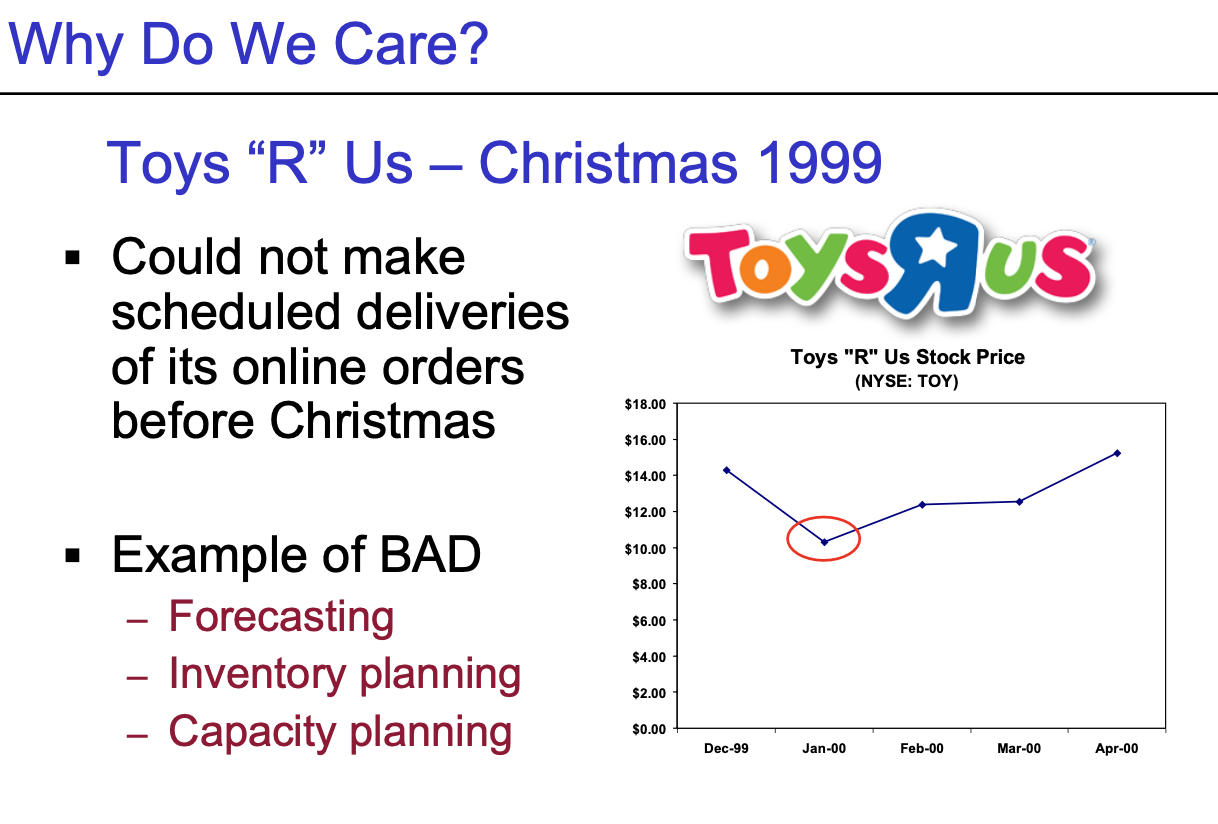
- Forecasting을 잘못할 경우 : 수요를 잘못 예측함
- 너무 많은 사람들이 몰릴 줄 예측 못함
- 물량 배송을 크리스마스까지 하지 못함
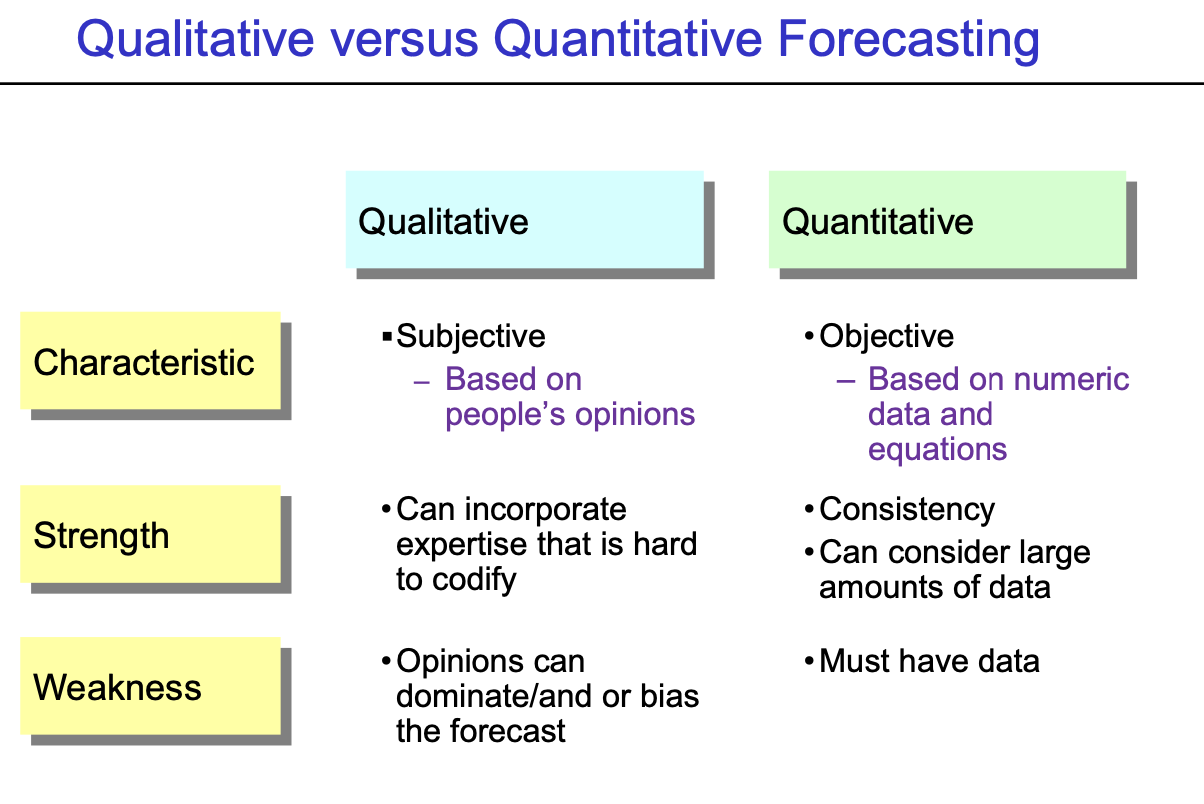
- Forecasting의 방법
- Qualitative : 정성적인 방법 (사람 머릿속에 있는 정보를 가져와서 예측하겠다)
- + : 머릿속에 있는 전문성 (숫자나 코드로 표현하기가 쉽지 않음), 어려운 현업의 노하우를 반영가능
- - : 한 두명의 의견에 의해 좌우될 수 있음 (과장)
- Quantitative : 정량적인 방법 ( 숫자에 의존하여 결정을 내리는 방법)
- + : 일관되게 이야기할 수 있음, 데이터가 많을 때 data를 충분히 활용하여 예측 가능
- - : Data가 없으면 사용하기가 힘듦
- 일반적으로는 Quantitative -> Qualitative 한 순서로 둘을 같이 사용
- Qualitative : 정성적인 방법 (사람 머릿속에 있는 정보를 가져와서 예측하겠다)
2. Time Series Methods
- Time Series Data
- 과거에 어떤 똑같은 event가 계속 있어서 그 정보가 누적이 되어있고 해당 정보를 활용해서 예측하는 것
- 과거가 결국 미래를 예측하는데 도움이 된다
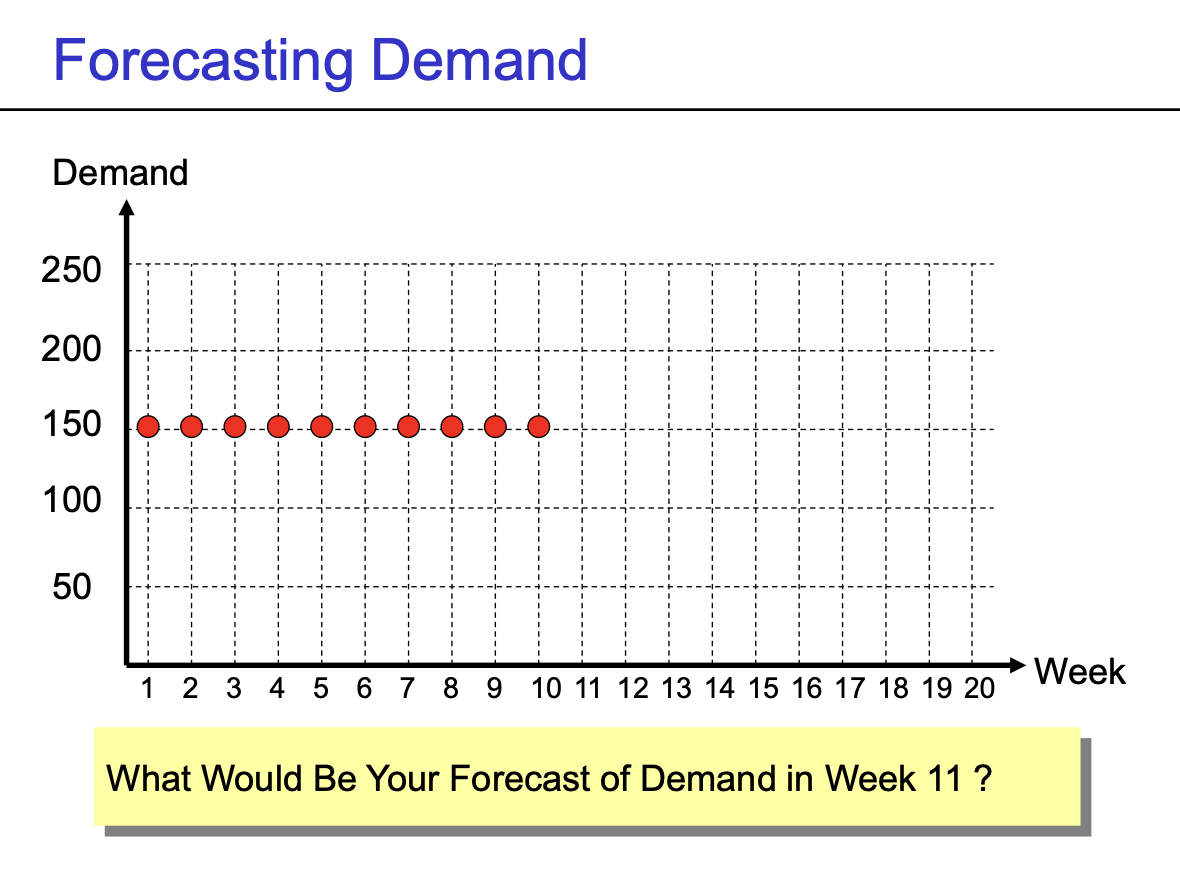
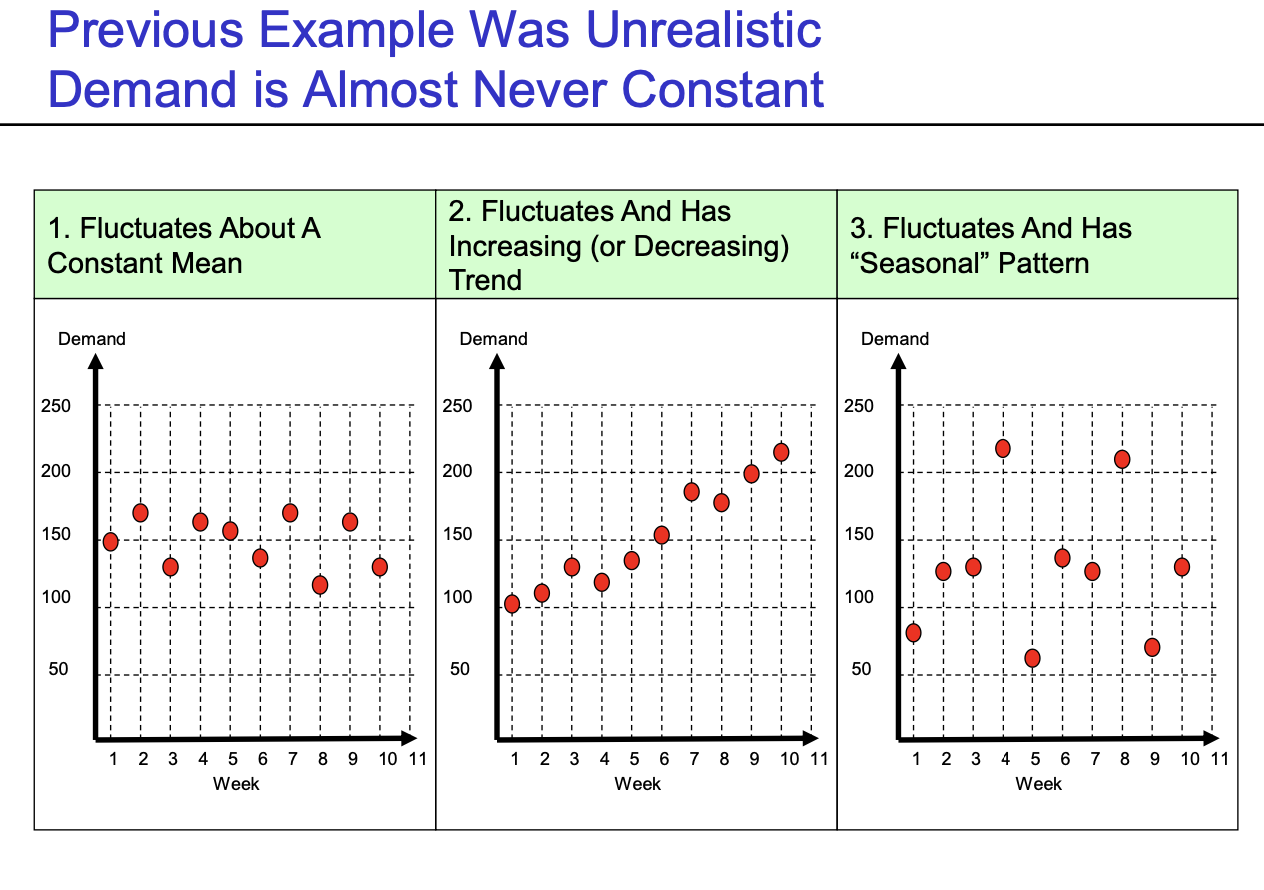
- Demand - Time 유형
- Fluctuates about a constant mean
- Fluctuates and has an increasing (decreasing) trend
- Fluctuates and has a "Seasonal" pattern
- Notations
- Actual Demand $A_{t}$ : 시각 t에 관찰된 수요
- Forecast $F_{t+1}$ : 시각 t에 시각 t+1에 대한 수요예측
- Type 1
- Fluctuates about a constant mean
- $Demand = Mean + Random Fluctuation $
- $E[Random Fluctuation] = 0$
- Methods
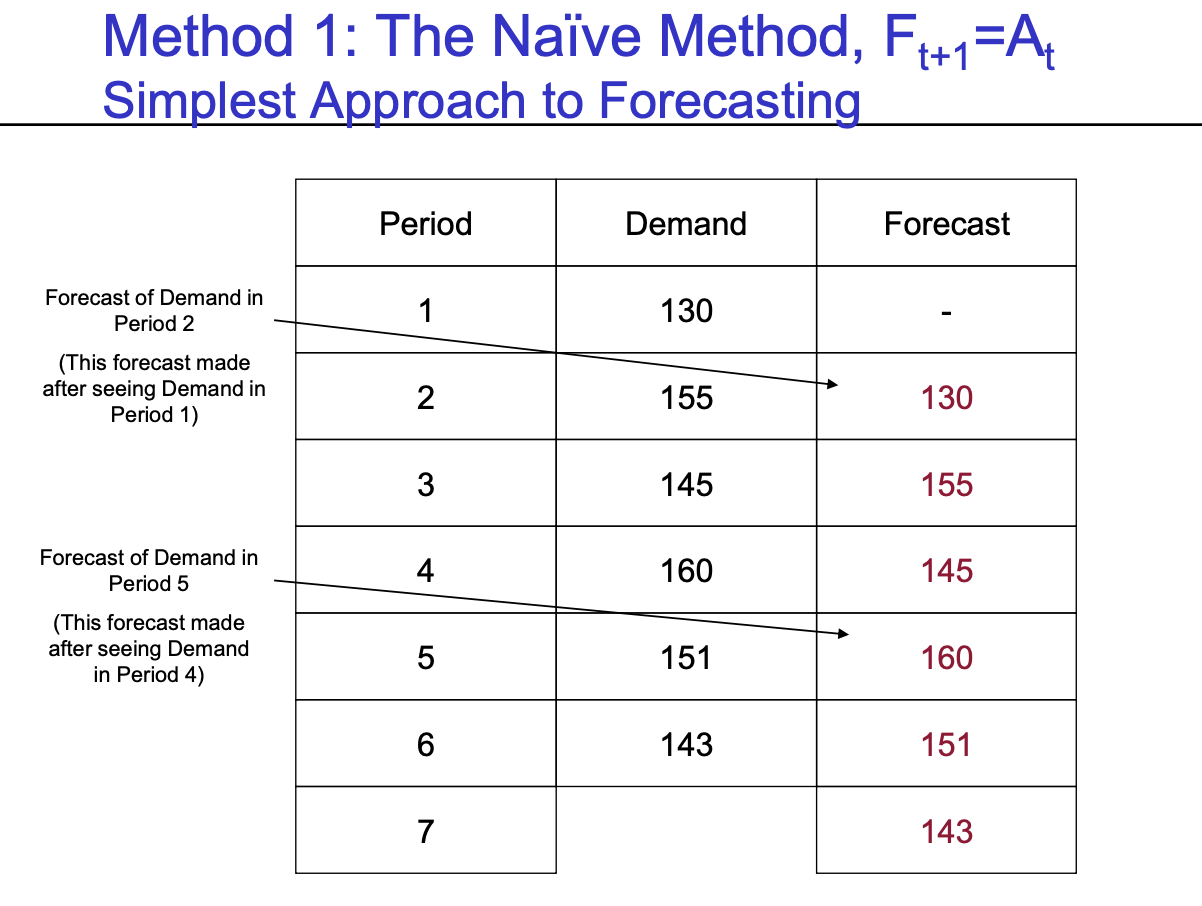
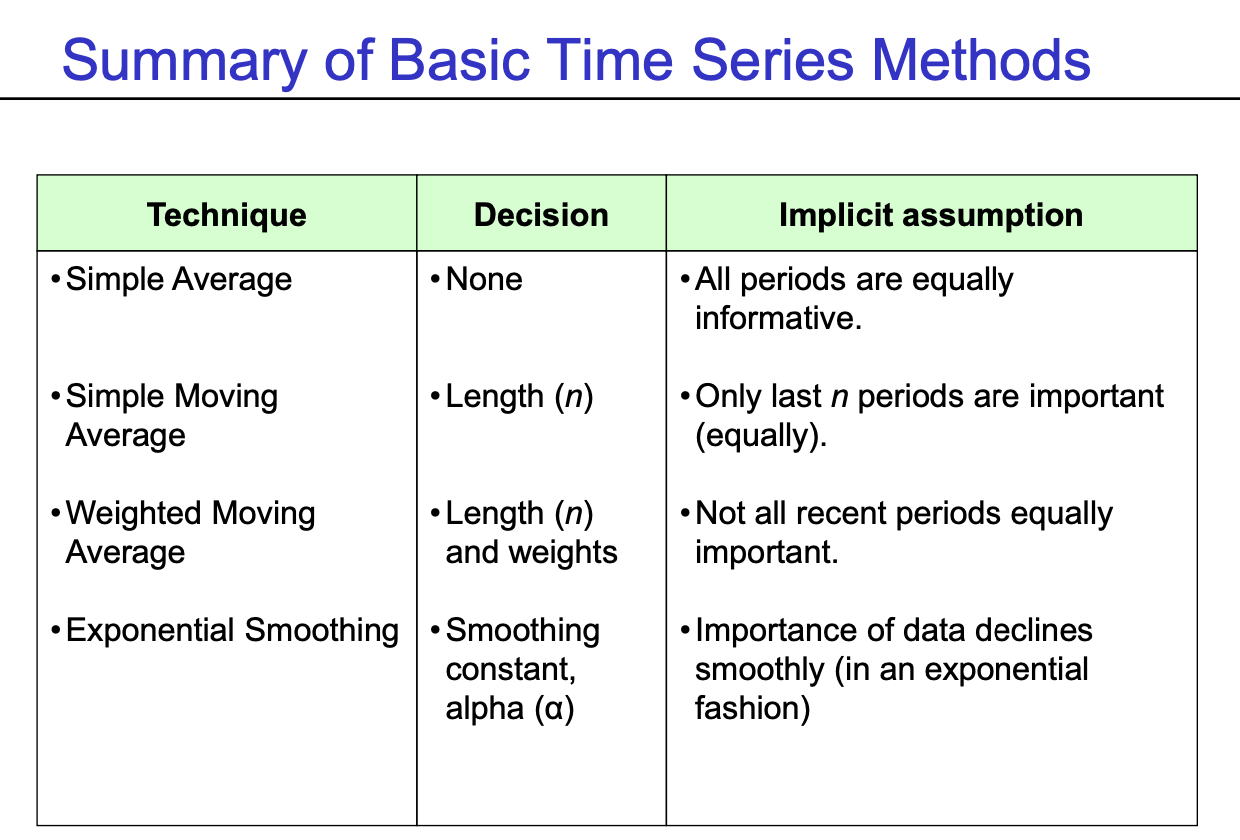
- Method 1 (The Naive Method) : $F_{t+1} = A_{t}$
- 너무 Naive하고 간단한 방법
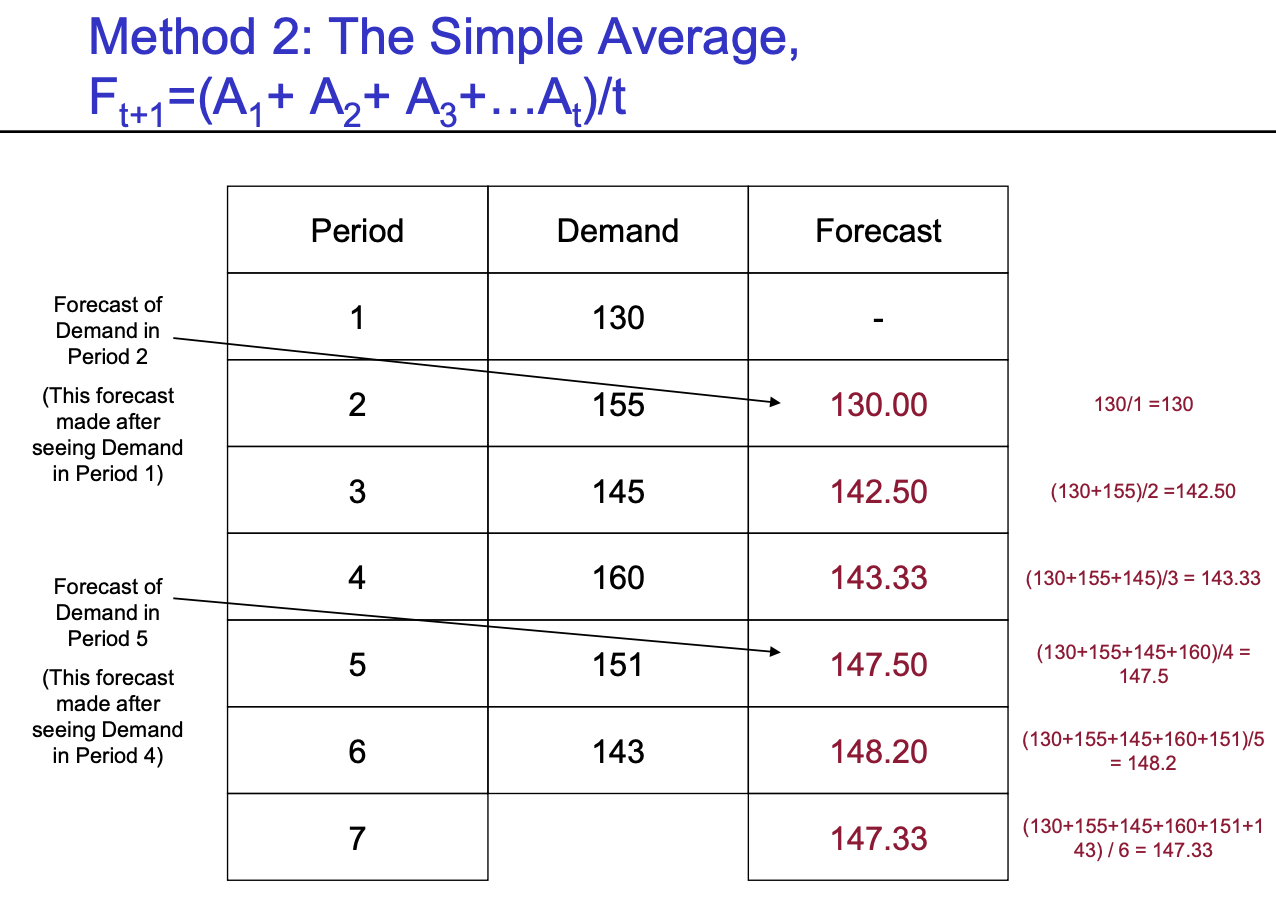
- Method 2 (The Simple Average) : $F_{t+1} = \frac {(A_{1}+A_{2}+A_{3}+....+A_{t})} {t}$
- 너무 outdated된 정보까지 고려해야 하는가? (10,9,8년전의 data를 사용하는 것이 효과가 있는가?)
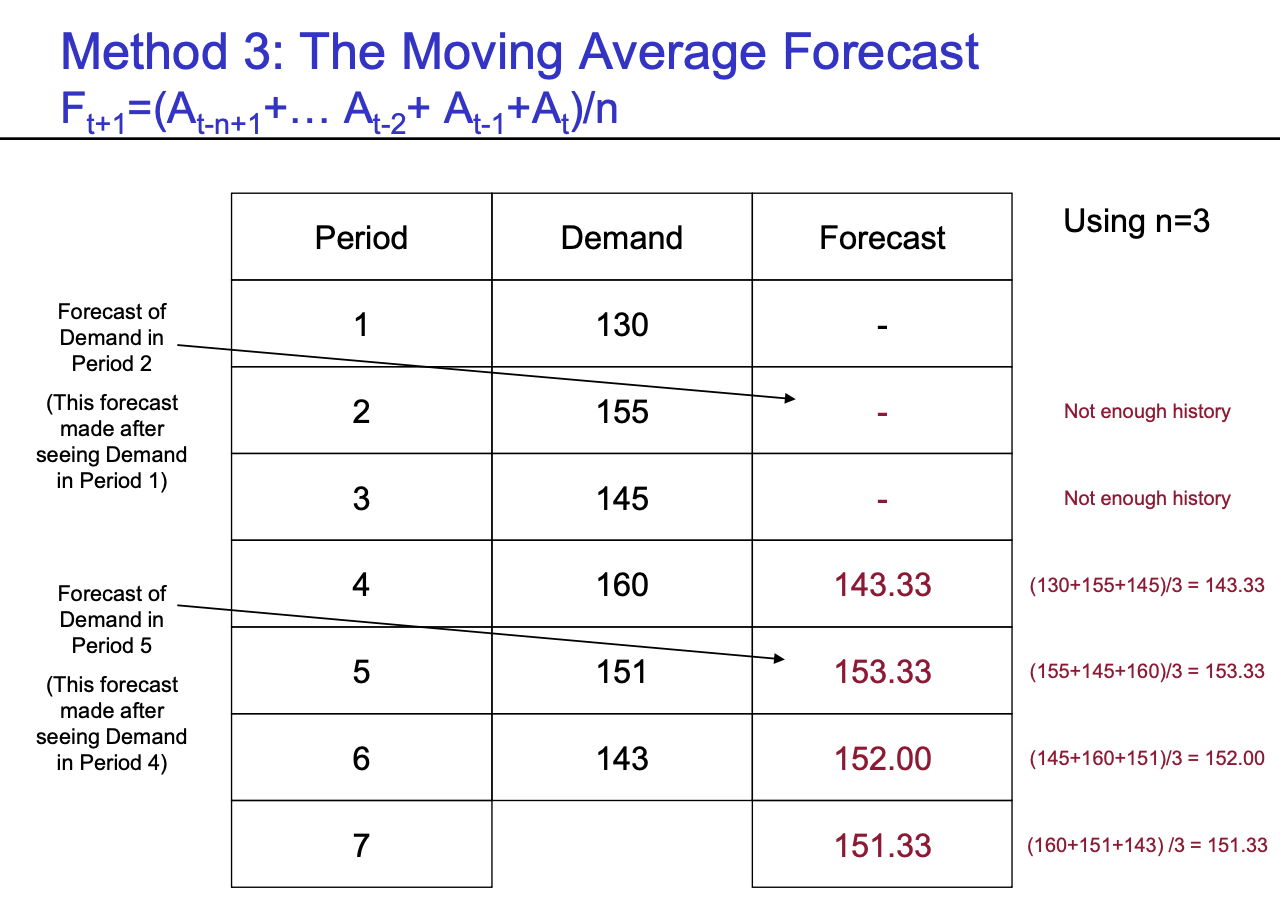
- Method 3 (The Moving Average Forecast) : $F_{t+1} = \frac {(A_{t-n+1}+...+ A_{t-2} + A_{t-1} + A_{t})} {n}$
- N most recent period : 과거의 N개의 정보만 가지고 수요예측을 하겠다는 의미
- 최근 data라고 해도, 똑같은 가중치를 두고 활용하는 것에 대한 의구심
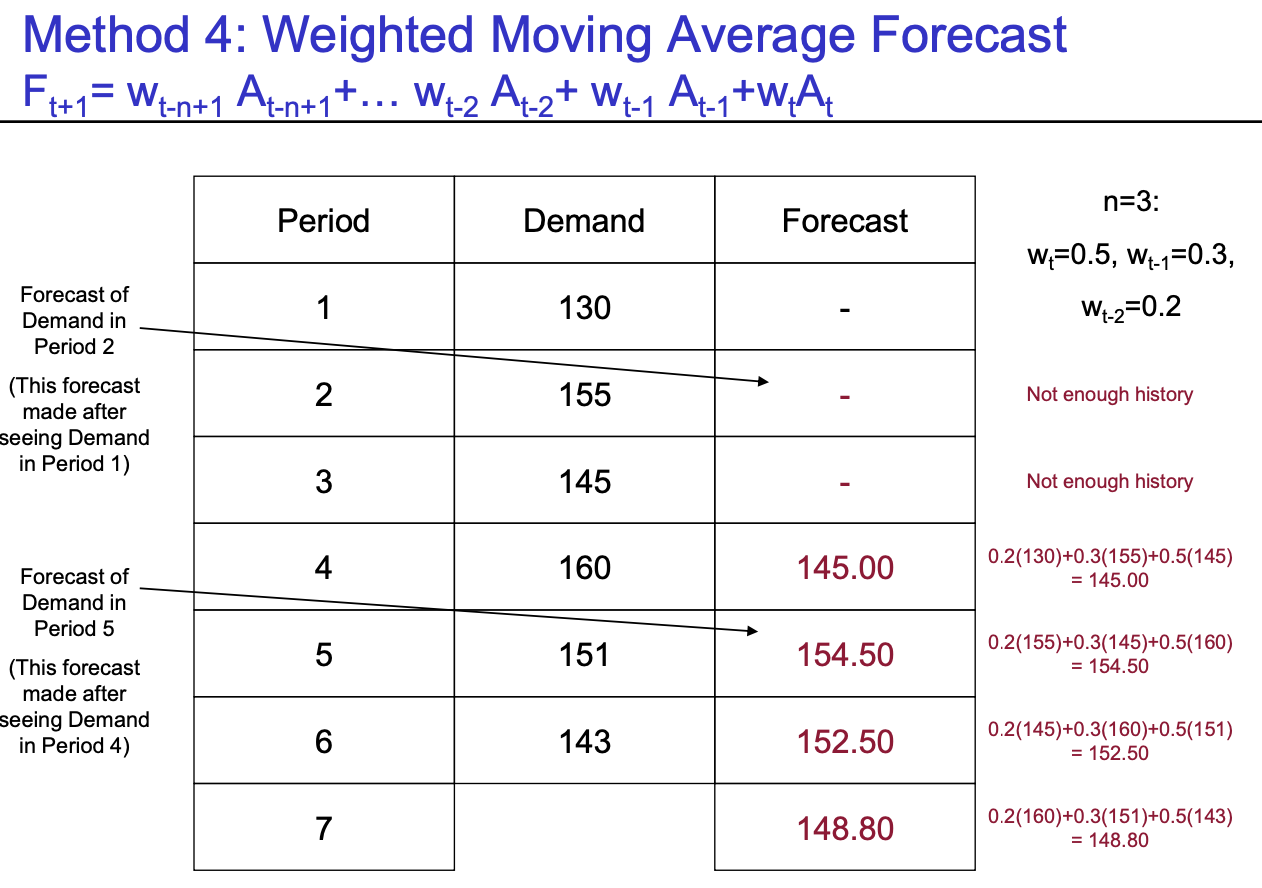
- Method 4 (The Weighted Moving Average Forecast) : $F_{t+1} = w_{t-n+1}A_{t-n+1} +.... + w_{t-2}A_{t-2} + w_{t-1}A_{t-1} + w_{t}A_{t}$
- 각 period마다 부여하는 가중치 weight가 다르다
- $\sum weight = 1$
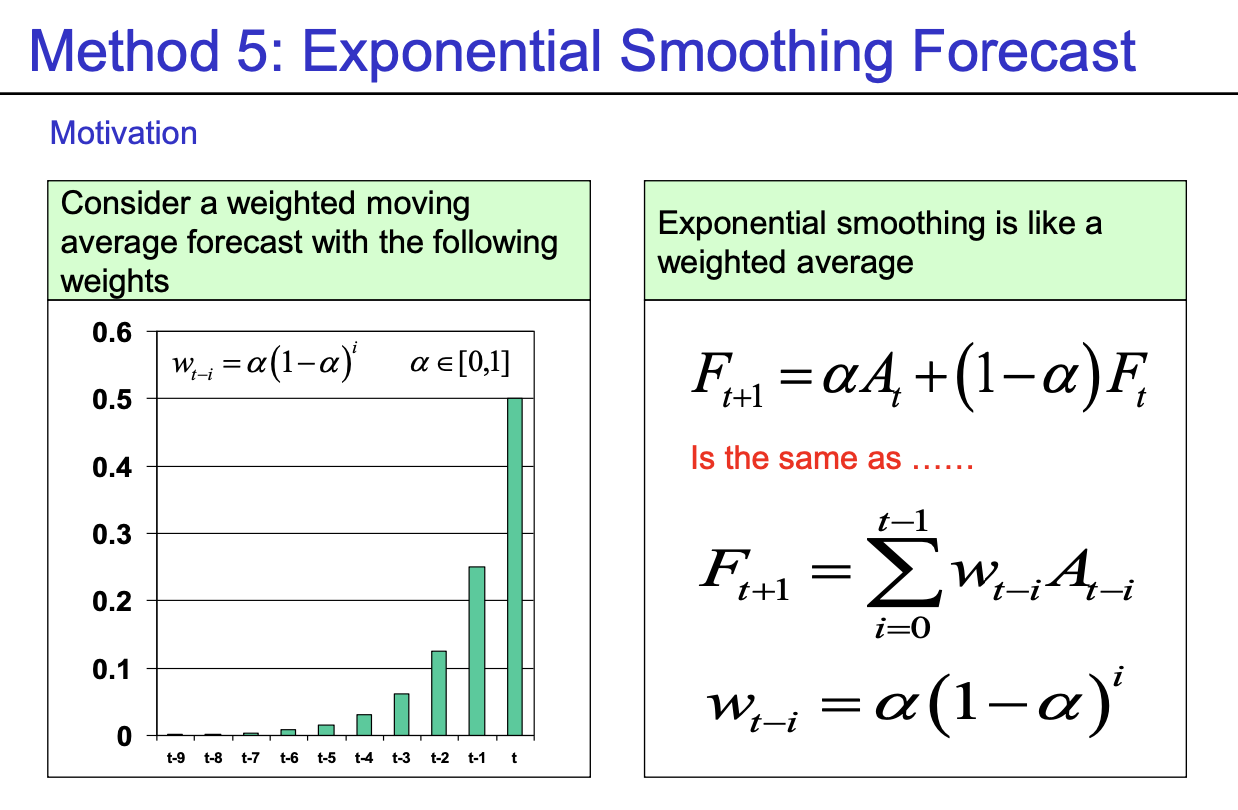
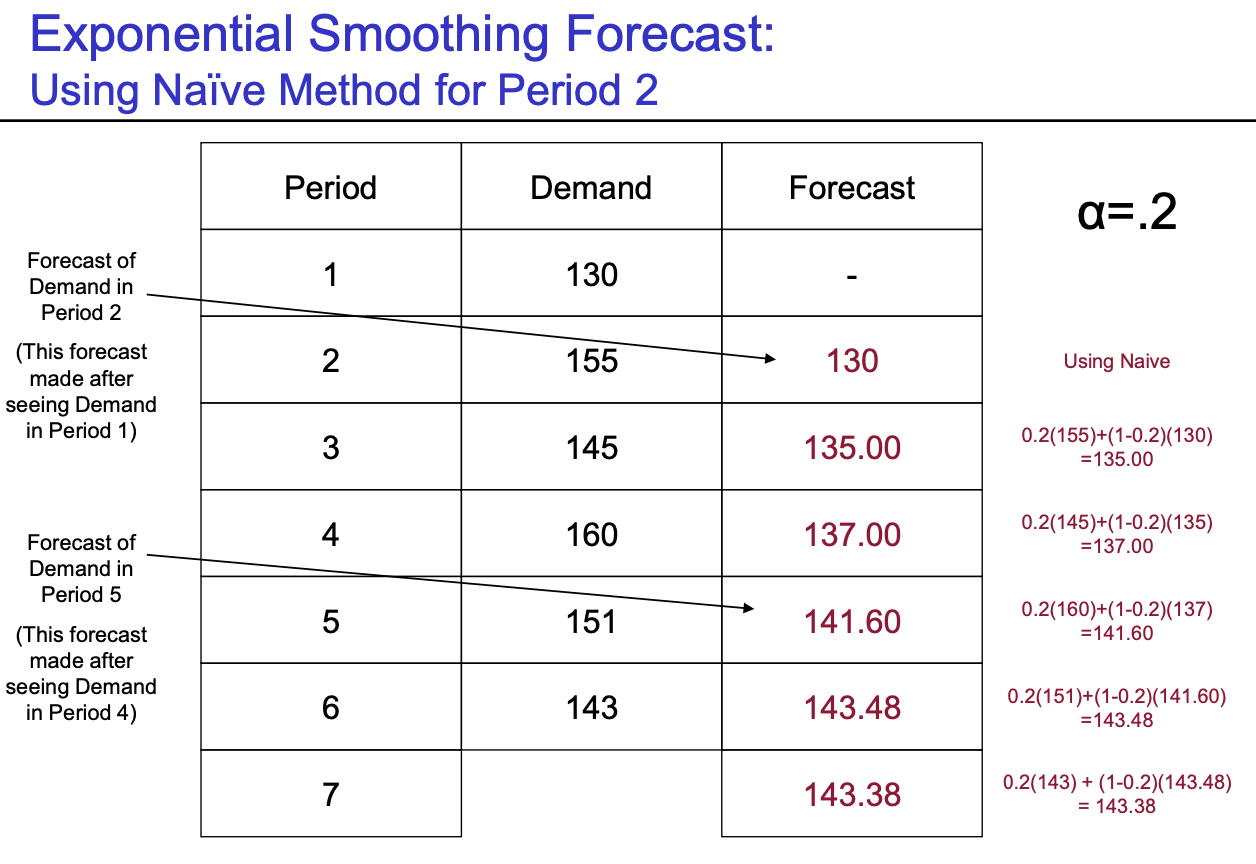
- Method 5 (Exponential Smoothing Forecast) :$F_{t+1} = \alpha A_{t} + (1-\alpha)F_{t}$
- $F_{t+1} = \sum_{i=0}^{t-1} w_{t-i}A_{t-i} $
- $ w_{t-i} = \alpha (1-\alpha)^{i}$ 위 2개의 식과 동일
- Smoothing Factor = $\alpha \in [0,1]$ : 최근 값의 demand에 가중치를 높게 둠
- 모든 historical data를 전부 사용 & weight을 내가 전부 다르게 부여
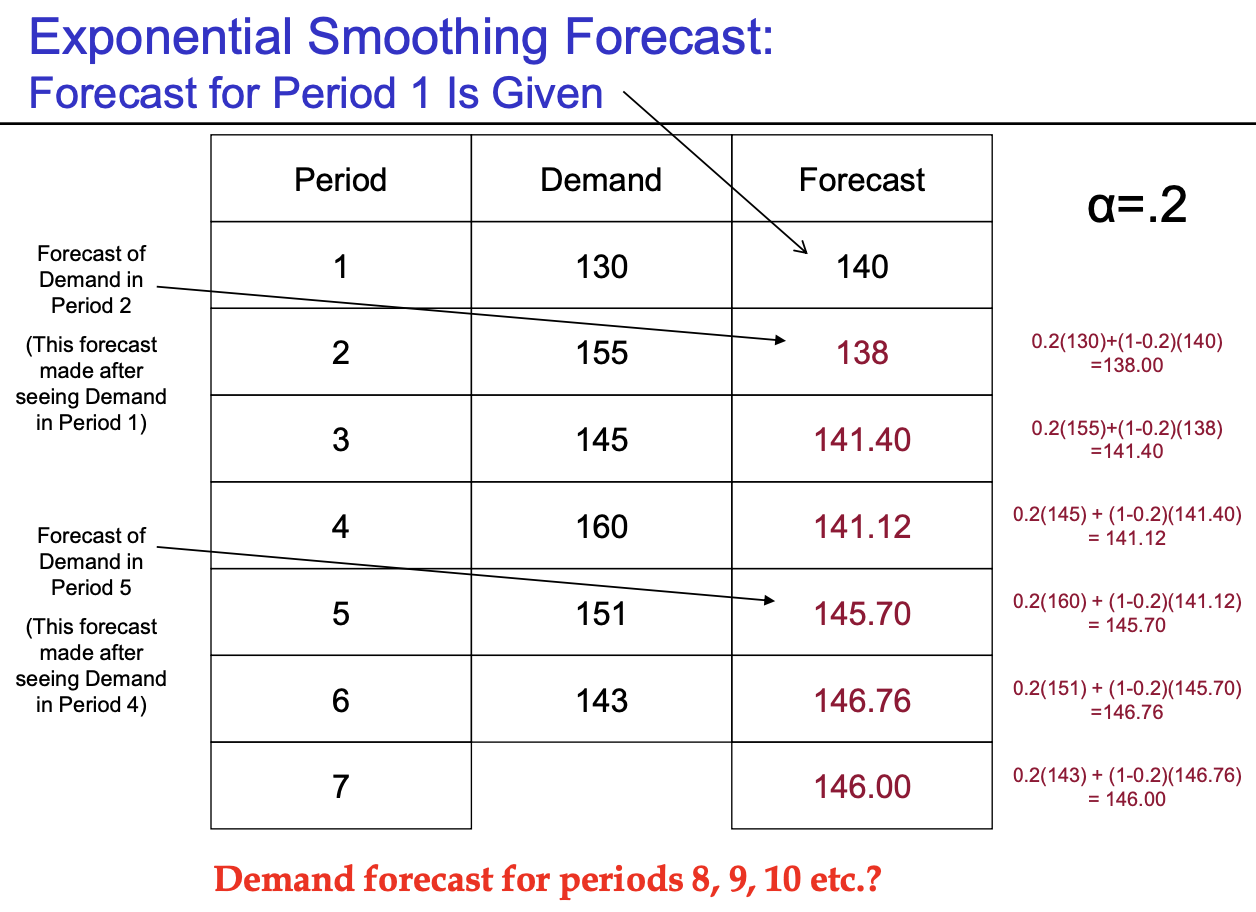
- What if Mean Demand Level Shifts as Some Point in Time?
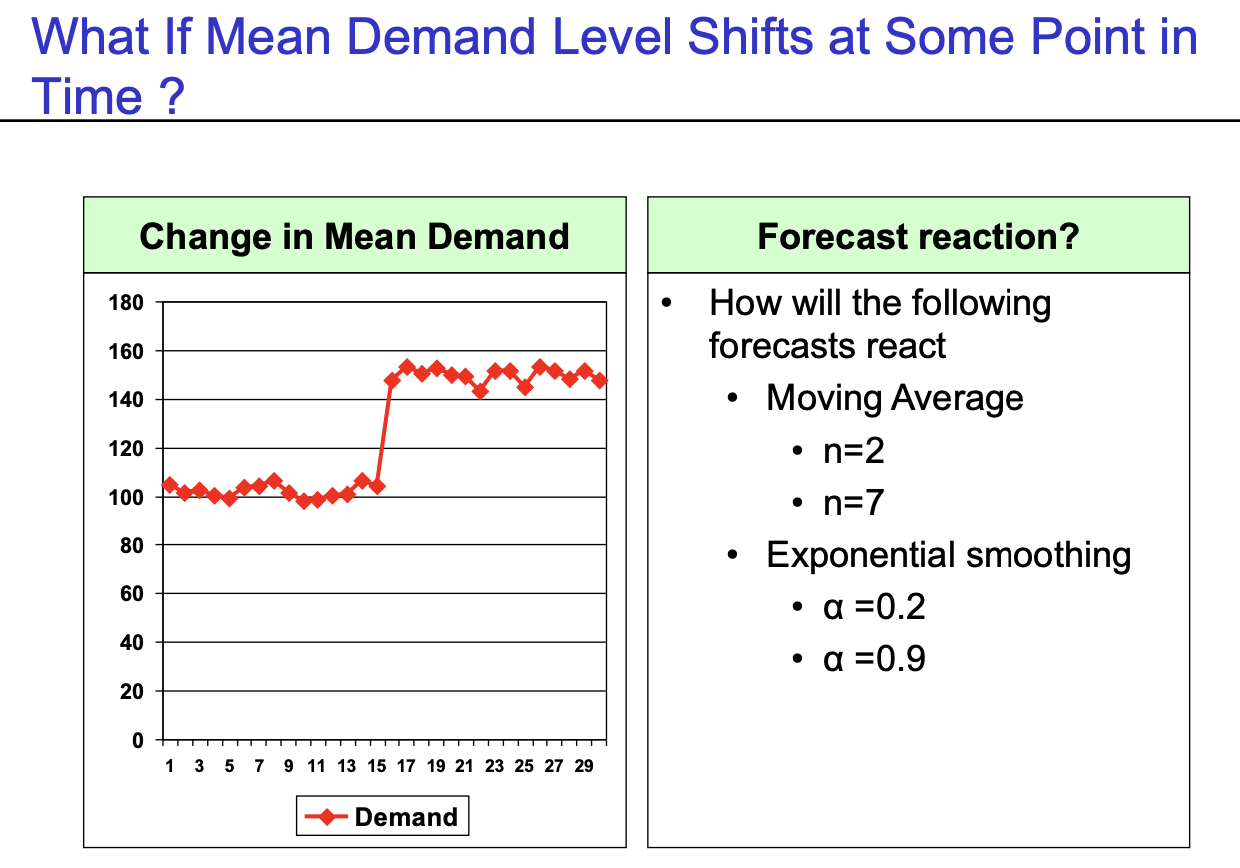
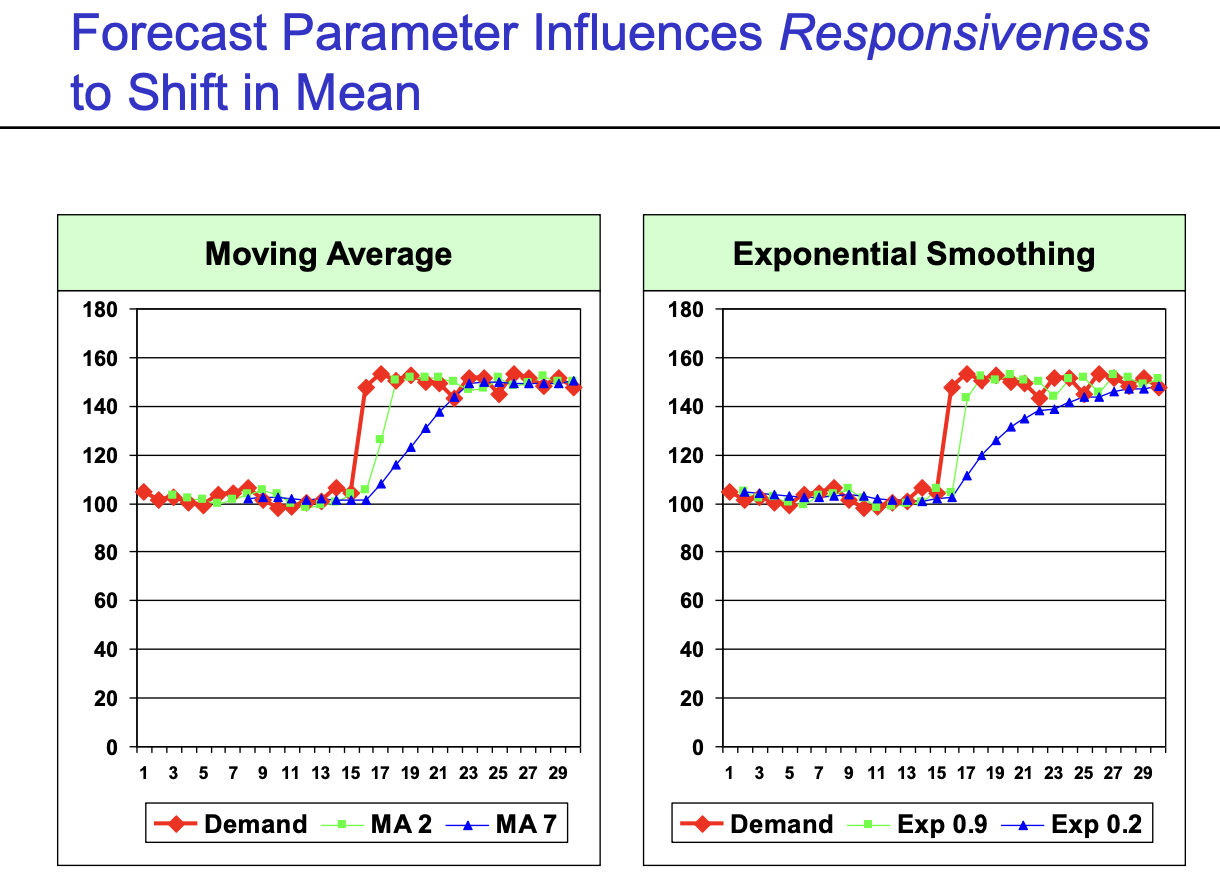
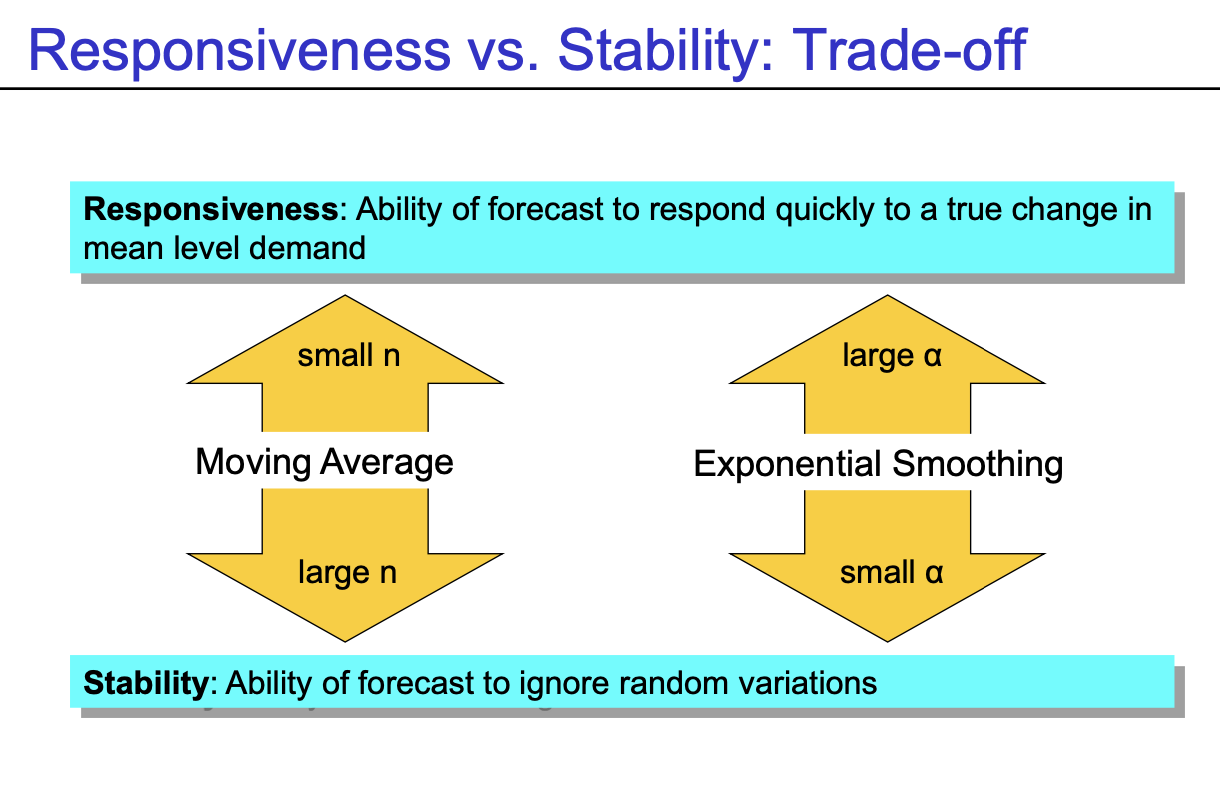
- Moving Average : n이 작을수록 반영하는 속도가 빠르다
- Exponential Smoothing : smoothing factor이 클수록 반영하는 속도가 빠르다
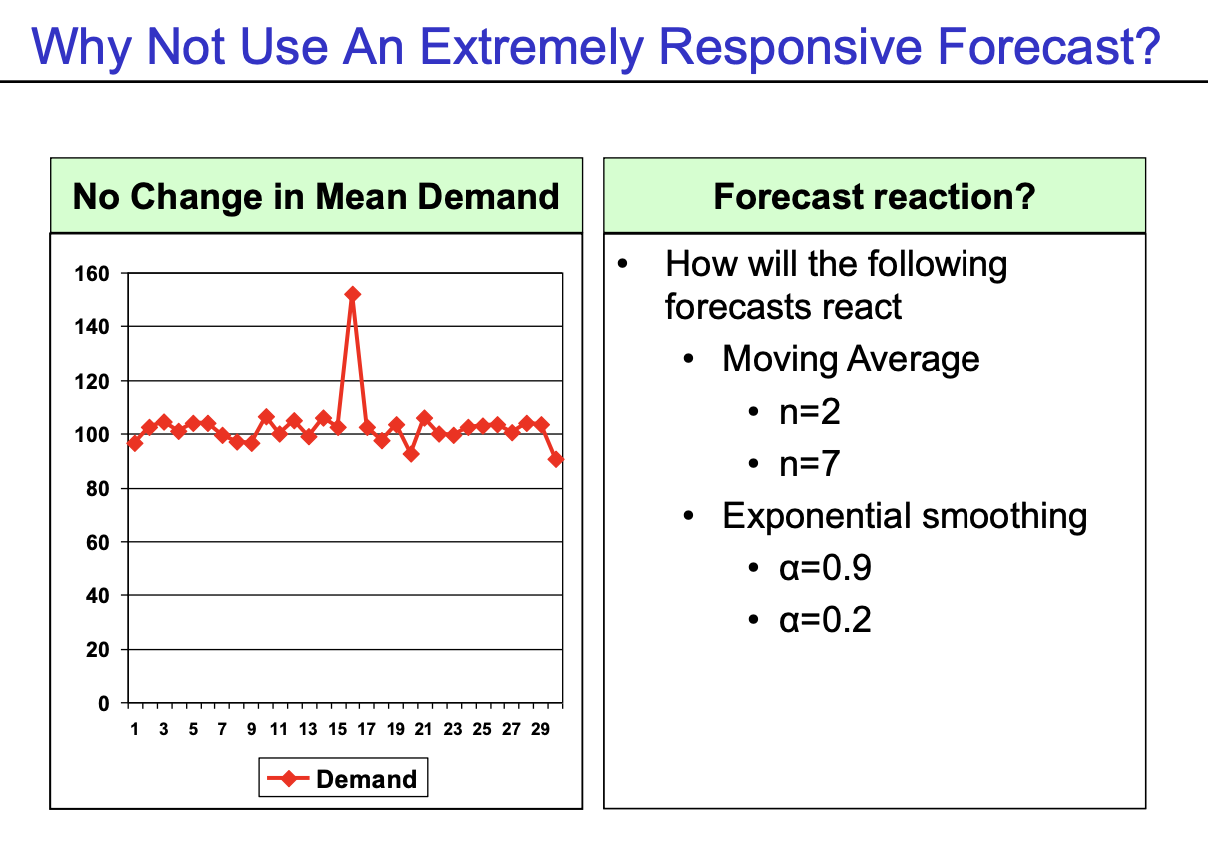
- Extreme Shift가 평균을 확 바꾼건지, 일시적으로 shift된 건지 구별하기가 어려움
- Moving Average : n이 클수록 크게 휘둘리지 않고 stable하게 유지
- Exponential Smoothing : smoothing factor이 작을수록 크게 휘둘리지 않고 stable하게 유지
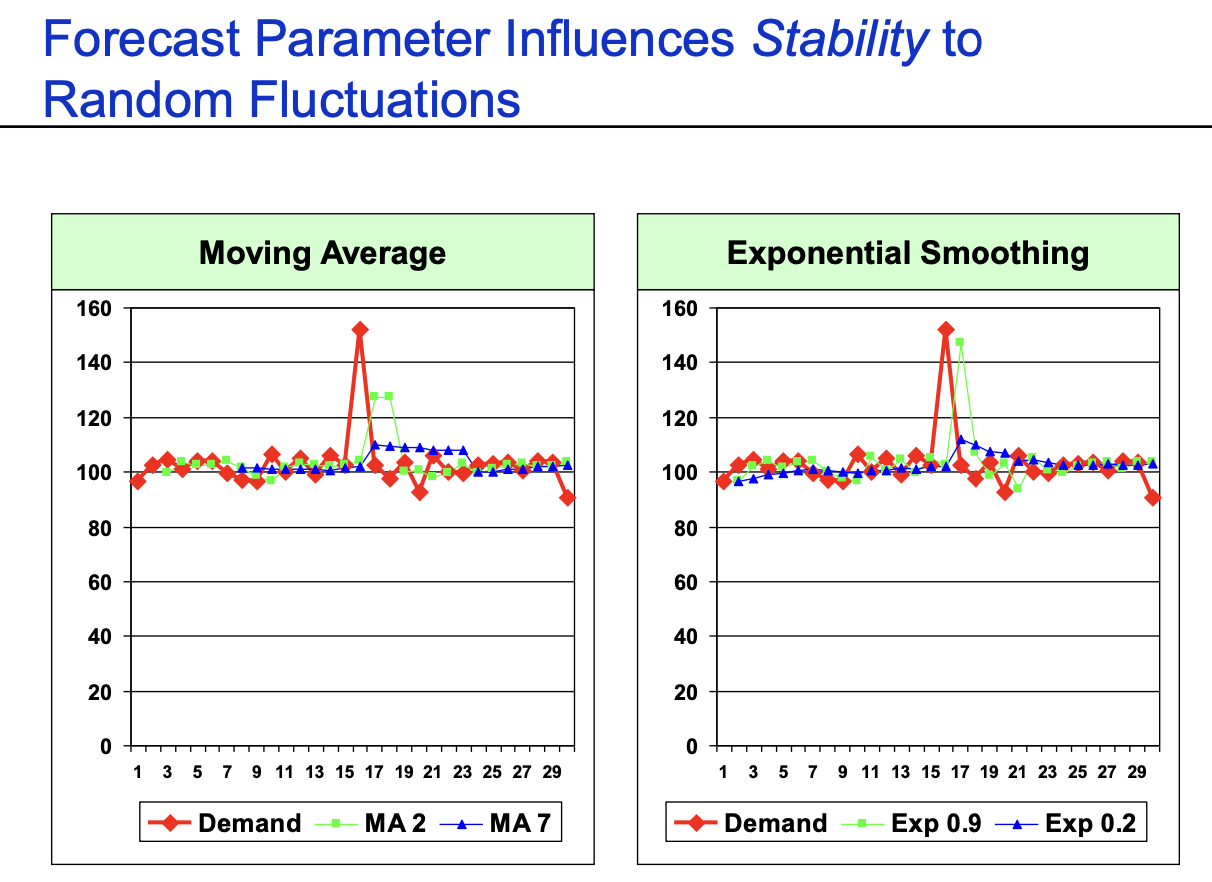
- Conclusion : 반응 속도 vs 안정성 둘 중에 하나를 선택해야 한다
3. Forecasting Errors
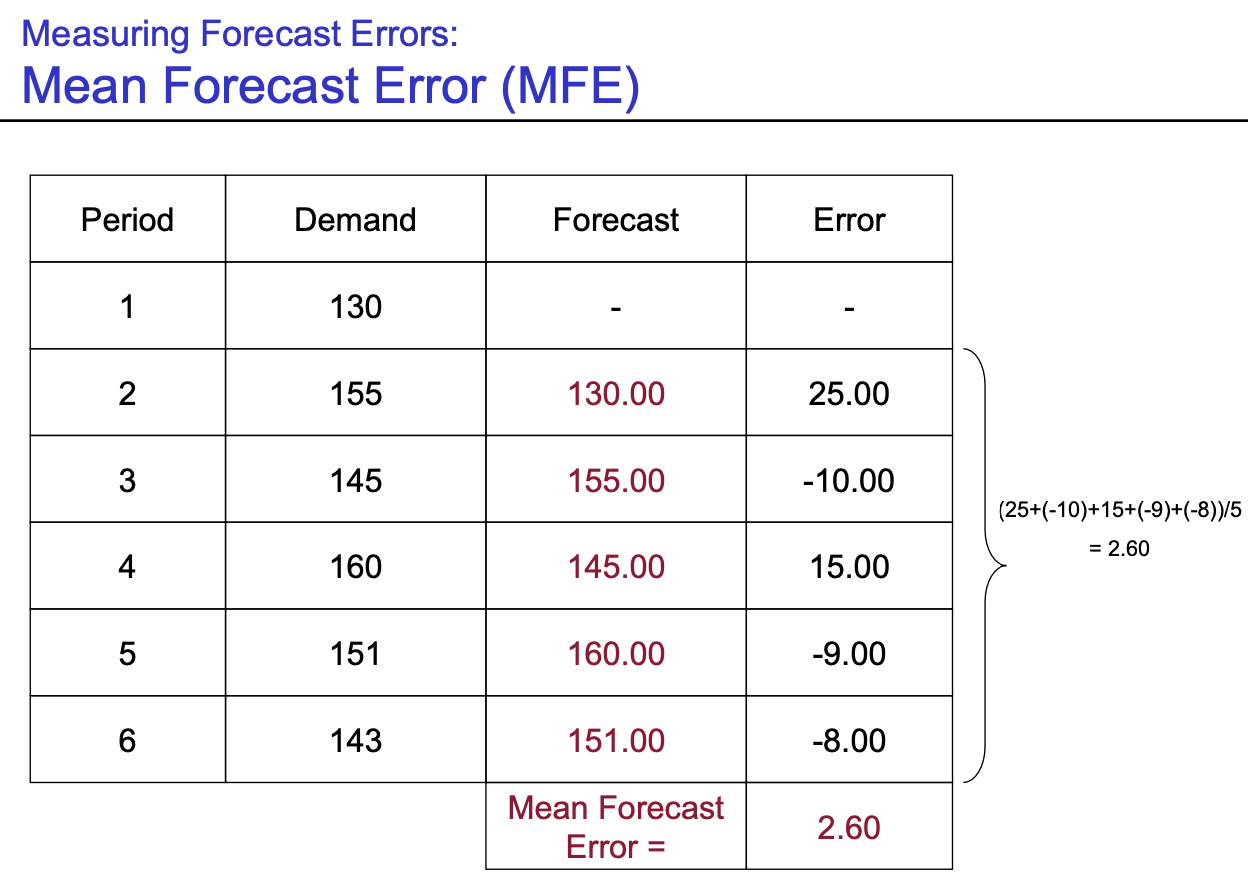
- $e_{t} = A_{t} - F_{t}$
- Forecast Error = Demand - Forecast
- MFE : $\frac {\sum error} {n}$ (부호를 고려하기 때문에 error 끼리 +/- 상쇄될 가능성이 있음)
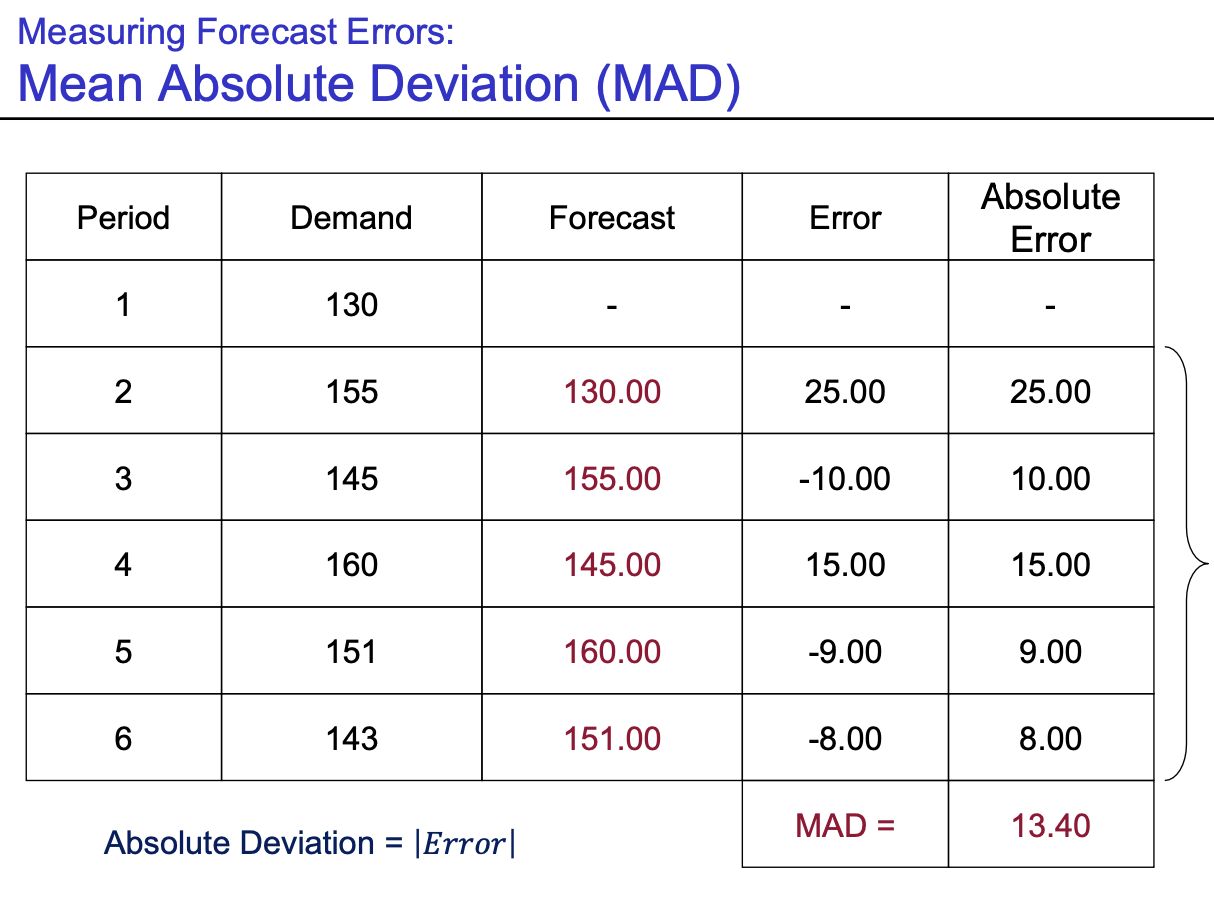
- MAD : $\frac {\sum |error| } {n}$ (error에 절댓값을 취한 후에 summation -> 평균 구하기)
- MSE : $\frac {\sum error^{2}} {n}$ (error에 제곱을 취한 후에 summation -> 평균 구하기)
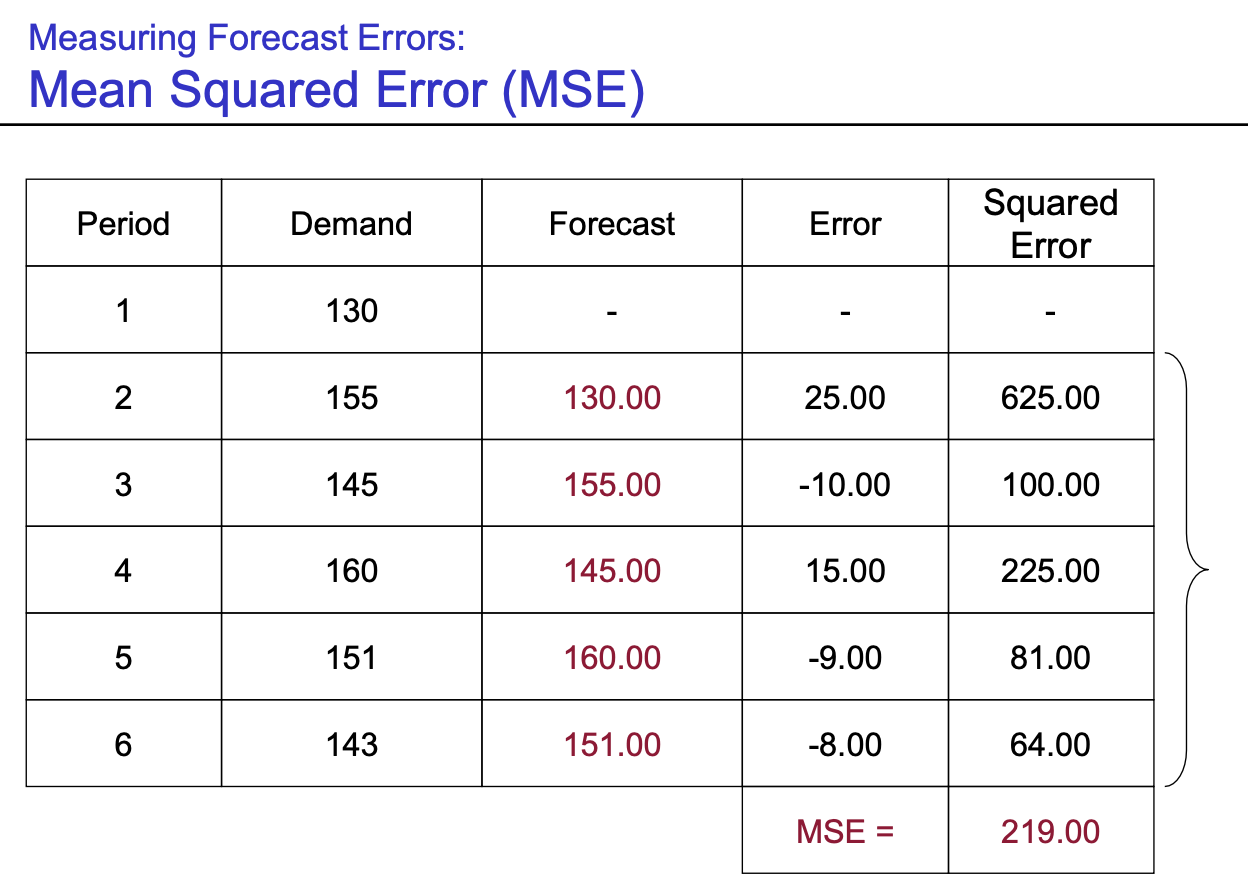
- MSE : error를 제곱하다 보니, error가 크면 penalty가 더 커짐 (과장시키는 효과)
- MAD : 모든 error를 equal하게 취급함 (반영비 or 가중치를 모두 동일하고 두고 싶을 때 사용)
- value 자체로 MAD끼리 비교할 수 없음 : 표본 혹은 기준이 다르면 같은 값이라도 다른 의미 (Scale 고려 X)
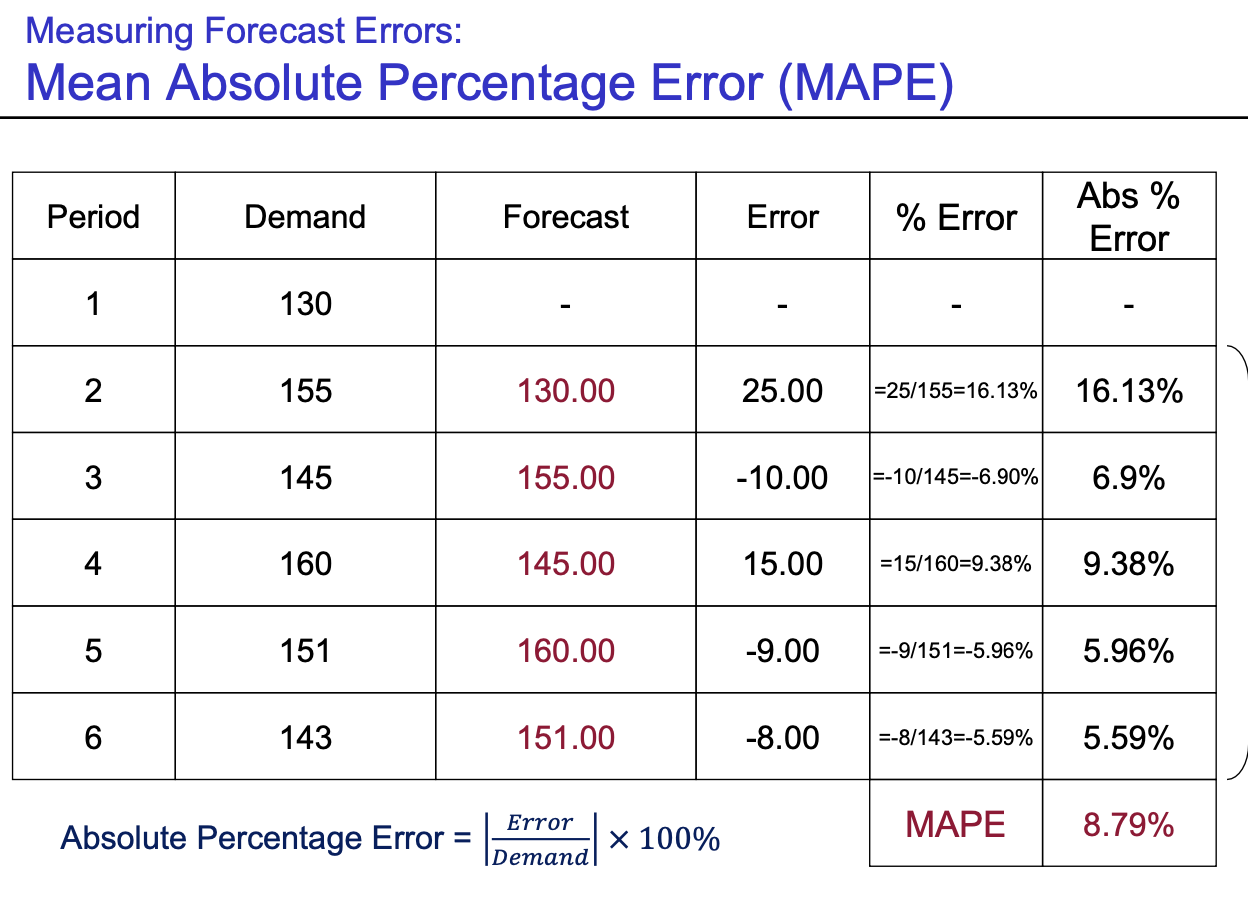
- Scale 고려 : Mean Absolute Percentage Error (MAPE)
- $MAPE = \frac {\sum \left|\frac{Error}{Demand} \right| \times 100%} {n}$
728x90
