728x90
1. Optimization
- Machine Learning model을 학습한다고 했을 때, Optimization 문제로 구성됨
- Model의 좋은 Parameter를 찾는 과정
- 특정 Optimization 문제의 solution이 되는 경우가 많음

- Optimization의 종류
- Unconstrained Optimization (제약식이 존재하지 X)
- Constrained Optimization (제약식이 존재 O)
- Convex Optimization

- Optimization Model의 구성요소
- 외부의 data인 parameter를 이용하여 구성한 Optimization model을 통해 모든 Constraints를 만족하는 decision variable들 중에 objective function을 최대화 / 최소화 시키는 decision variable의 값을 구하기
- Decision Variables : 의사결정변수
- Objective Function : 목적함수
- Constraints : 제약식
- Parameters : 상수(Const)
- Feasible Solution : 모든 constraints를 만족하는 의사결정 변수들의 조합
- Feasible Set : 모든 feasible solution들의 집합
- Optimal Solution : feasible solution 중에서 objective function을 최대화 / 최소화하는 solution
- 외부의 data인 parameter를 이용하여 구성한 Optimization model을 통해 모든 Constraints를 만족하는 decision variable들 중에 objective function을 최대화 / 최소화 시키는 decision variable의 값을 구하기


2. Optimization using gradient descent
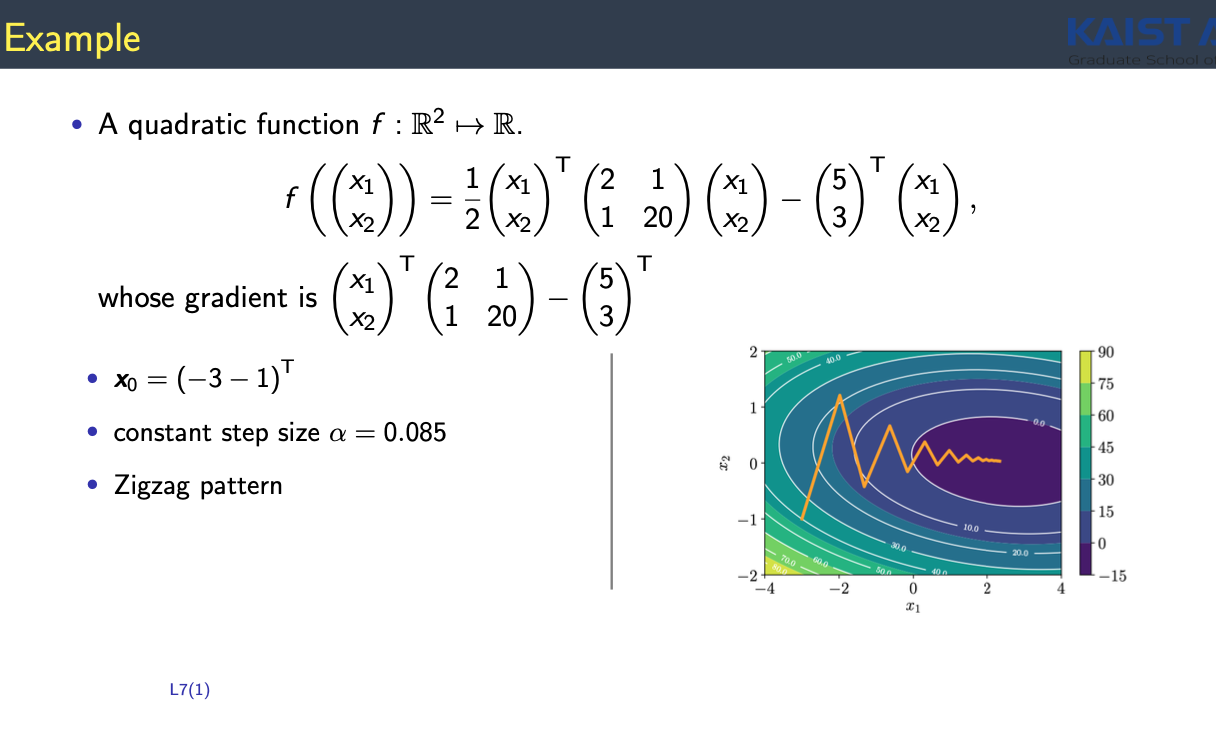
- $d_{k}$를 gradient와 반대방향으로 아무렇게나 잡고, step size $\gamma _{k}$를 잘 조정하기만 하면 항상 이 함수 $f(x)$를 최소화하는 다음 update된 값 $x_{k+1}$을 구할 수 있음
- Steepest gradient descent : $\nabla f(x) \cdot d <0$ 을 만족하는 d 중에 $\nabla f(x)$의 반대방향으로 d를 선택하는 것이 steepest GD라 한다

- Objective Function은 어떤 data로부터 정해지는 경우가 많음
- L : loss function
- $theta$ : parameter
- $L$이라는 function을 얼마만큼의 data로 정의하느냐에 따라 구분됨
- Batch gradient descent (entire n)
- Mini-batch gradient descent (k < n data)
- Stochastic gradient descent (k < n data with unbiased gradient estimation)
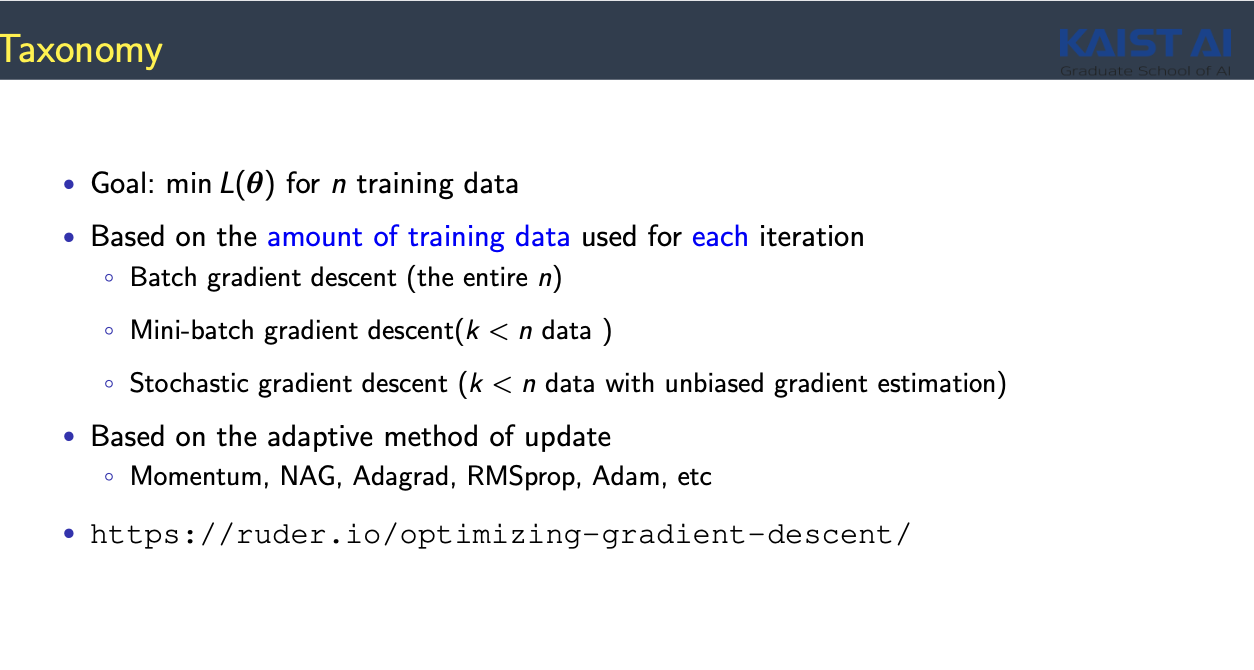
- Stochastic Gradient Descent
- Loss function : Data point에 대한 loss의 summation으로 표시
- 현재 parameter를 gradient와 반대 방향으로 업데이트
- $\Theta _{k+1} = \Theta _{k} - \gamma _{k} \nabla L(\Theta _{k})^{T} = \Theta_{k}- \gamma_{k}\sum_{n=1}^{N}\nabla L_{n}(\Theta_{k})^{T}$
- 매 update 순간마다 $\sum_{n=1}^{N}\nabla L_{n}(\Theta_{k})^{T}$ 를 계산하는 것이 매우 계산량이 많음
- Batch Gradient : Gradient를 모든 data point를 다 고려해서 계산하는 update
- original full batch gradient의 noisy apporximation : mini-batch GD, SGD
- Data가 매우 많은 상황 = 전체 gradient를 구하기 힘든 상황
- Mini-batch gradient : data point가 n개 있으면 그 중 특정 subset을 구해서 그 subset에 있는 gradient만 계산해서 update
- Stochastic Gradient Descent : subset을 구할 때 이 subset을 구한 gradient의 expectation의 original full batch gradient와 동일하도록 (original batch gradient를 잘 근사할 수 있게 다음과 같은 방식으로 디자인하기)
- Batch Gradient : Gradient를 모든 data point를 다 고려해서 계산하는 update


- Step Size $\gamma$ : 적당하게 설정해야 함
- 너무 작게 설정 : update가 천천히 일어남
- 너무 크게 설정 : overshooting이 일어남 (converge하지 않음)
- Momentum with Gradient Descent
- $x_{k+1} = x_{k} - \gamma_{i} \nabla f(x_{k})^{T} + \alpha \Delta x_{k}$
- update 항 뒤에 추가항을 추가 : $\alpha \Delta x_{k}$
- $\Delta x_{k} = x_{k} - x_{k-1}$ : 그 전에 update 했던 방향
- 그 다음 방향으로 update할 때도 그 전에 update 했던 방향을 고려하자는 의미

3. Constrained Optimization and Lagrange Multipliers
- Constrained Optimization ($f(\tilde{x})$, constraints) -> Unconstrained Optimizations($L(\tilde{x}, \lambda, \nu$))
- Primal 문제를 푸는 것보다 Dual 문제를 푸는 것이 더 쉽다



- $\lambda, \nu$ : Lagrange multiplier
- all $\lambda \geq 0$, $\nu$는 제약 조건 없음
- constraint에 해당하는 조건마다 $\lambda, \nu$가 정의됨
- Lagrange dual function
- $\lambda, \nu$를 고정했을 때 x에 대한 lnfimum(하한)값을 칭함
- original optimization 문제는 x에 대한 함수, lagrange dual 함수는 $\lambda, \nu$에 대한 함수

- Feasible $\tilde{x}$ : 모든 constraints 를 만족하는 solution
- $g_{i}(\tilde{x}) \leq 0$, $h_{i}(\tilde{x}) = 0$
- Best lower bound 찾기
- maximize $D(\lambda, \nu)$
- $\lambda, \nu$ 에 대한 optmization
- Dual optimization은 항상 Convex optimization이 됨
- convex optimization은 항상 풀 수 있다!
- $D(\lambda, \nu)$ 가 always concave function이 된다

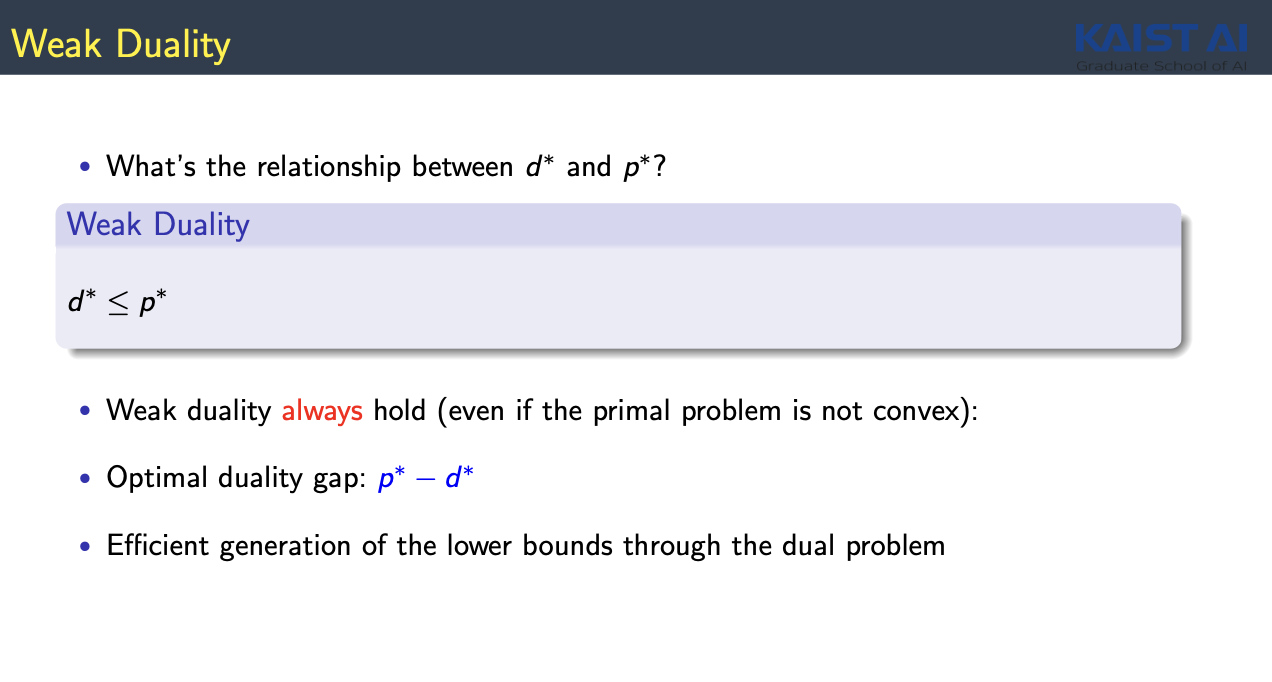
- Weak Duality
- Primal Optimization과 Dual Optimization간의 관계를 설명
- Primal Optimization은 풀기 힘들더라도 Dual Optimization은 항상 풀 수 있다
- Always $ d^{\ast} \leq p^{\ast}$
- $ d^{\ast}$ 의 값을 알면 $p^{\ast}$가 대략적으로 어느정도인지 예측이 가능함
- Duality Gap : $p^{\ast} - d^{\ast}$
4. Convex Set and Functions
- convex optimization
- f(x)라는 함수를 minimize
- $x \in X$ : constraint
- f(x) : convex function
- X: convex set
- convex function을 convex set을 constraint로 주고 하는 optimization
- 보통 Optimization 문제의 해결 여부는 해당 문제가 convex 인지의 여부로 거의 귀결됨

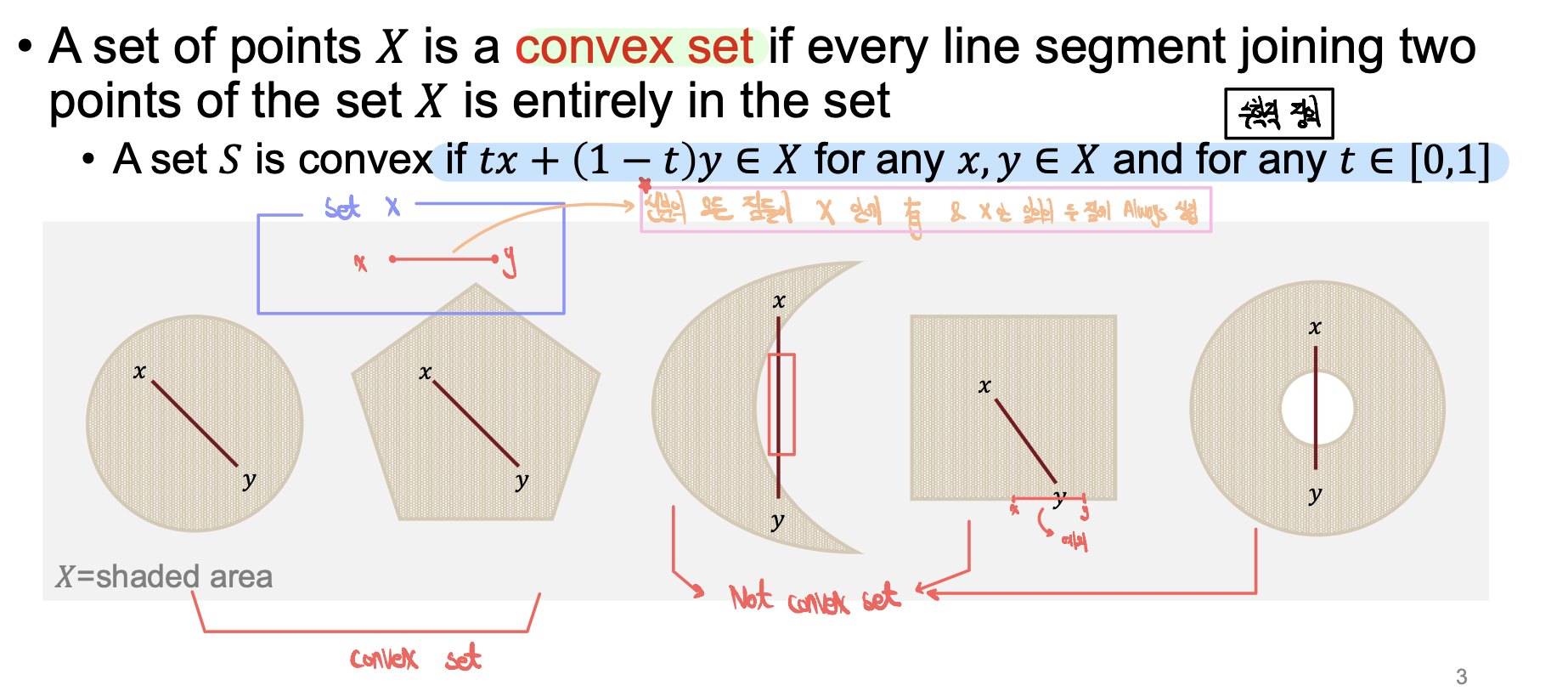
- Convex Set
- 선분안에 있는 모든 점들이 X안에 존재
- X 내부의 임의의 두 점에 대해 Always 성립

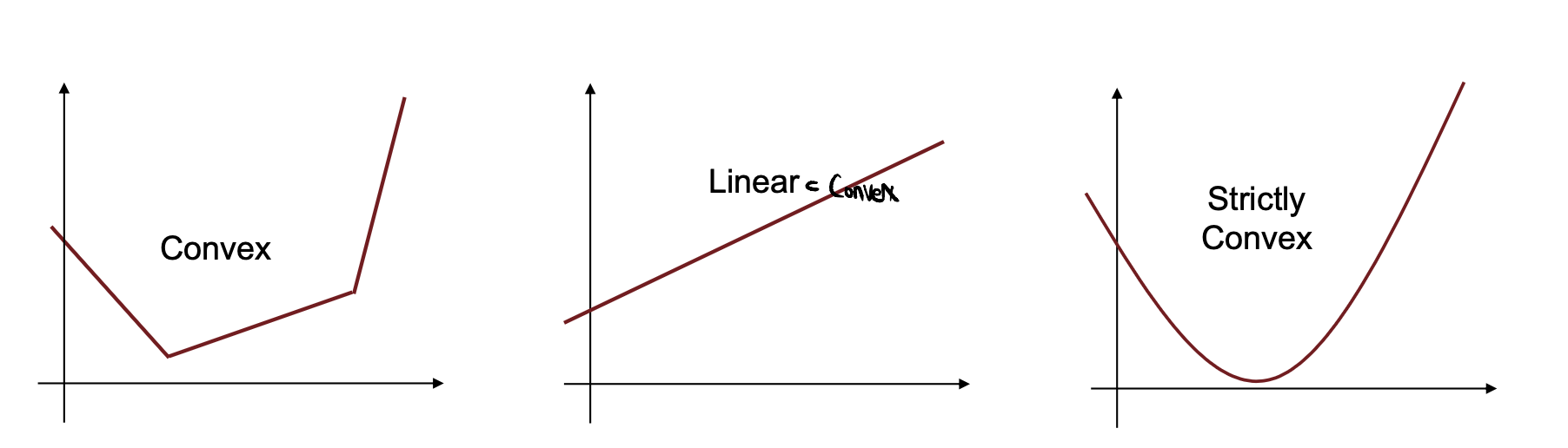
- Convex function : 아래로 볼록인 함수
- 두점을 잇는 임의의 line segment가 always function보다 위에 존재
- affine functions(ex.linear function)들은 concave & convex 동시에 만족
- strictly convex : 등호 제거 (직선 구간 존재 X)
- 함수를 minimize 하는 point와 $\nabla f(x) = 0$인 point와 동치



- Conditions
- first - order condition : 접선이 always 직선 아래 존재
- second - order condition : Hessian Matrix가 PSD
- 위의 두 정의는 서로 동치이다





5. Convex Optimization
- f(x) : convex function
- g(x) : convex function
- linear conditions: convex 조건들

- Strong Duality
- $d^{\ast} = p^{\ast}$
- KKT conditions
- KKT Conditions
- $x^{\ast}$ : Primal optimization solution
- $\lambda^{\ast}, \nu^{\ast}$ : Dual optimization solution
- 어떠한 optimization problem 경우에도 KKT가 필요조건
- convex optimization의 경우 KKT가 충분조건도 됨 : 필요충분조건
- 어떤 $ x, \lambda, \nu$가 해당 조건을 만족한다면 Primal, Dual의 optimum이 된다
- $\lambda^{\ast}, \nu^{\ast}, x^{\ast}$ 가 아래의 조건을 만족한다면 : KKT 조건을 만족했다고 함



728x90
