[Python ML Guide] Section 5.3(회귀 Regression): Linear Regression & Evaluation (평가지표) / Boston 주택 가격 예측

https://www.inflearn.com/course/%ED%8C%8C%EC%9D%B4%EC%8D%AC-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EC%99%84%EB%B2%BD%EA%B0%80%EC%9D%B4%EB%93%9C

[개정판] 파이썬 머신러닝 완벽 가이드 - 인프런 | 강의

 

 

---

1. LinearRegression Class

 

 

LinearRegression Class

 

class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=-1)

 

• Regulation(규제)를 적용하지 않은 모델
• LinearRegression 클래스는 실제값과 예측값의 RSS(Residual Sum of Squares)를 최소화하는 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스임
• LinearRegression 클래스는 fit() method으로 X, y 배열을 입력받으면 회귀 계수(Coefficients)인 W를 coef_ 속성에 저장

 

 

 

 

 

입력 파라미터

 

• fit_intercept: boolean값으로 True가 default, intercept($w_{0}$ = bias = 절편) 값을 계산할 것인지 말지를 지정함, False로 지정하면 intercept가 사용되지 않고 0으로 지정됨 (y절편이 0이라 원점을 지나는 직선)
• normalize: boolean 값으로 False가 default, fit_intercept가 False인 경우에는 이 파라미터가 무시됨. 만일 True이면 회귀를 수행하기 전에 입력 데이터 세트를 정규화한다
  • 되도록이면 해당 파라미터를 쓰지 말고 미리 전처리 과정에서 min-max scalar 혹은 standard scalar를 사용하는 것이 맞음

 

 

 

속성

 

• coef_: fit() method를 수행했을 때 회귀 계수가 배열 형태로 저장하는 속성. Shape는 (Target 값 개수, Feature 개수)이다
• intercept_: intercept 값

 

 

 

 

선형 회귀의 종류

 

• 일반 선형 회귀: 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제(Regularization, RSS를 무뎌지게 하는 방법)를 적용하지 않은 모델
• 릿지(Ridge): 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델
• 라쏘(Lasso): 라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식
• 엘라스틱넷(ElasticNet): L2, L1 규제를 함께 결합한 모델
• 로지스틱 회귀(Logistic Regression): 회귀라는 이름이 붙어있지만, 사실은 분류에 사용되는 선형 모델 (0,1의 이산값을 예측

 

 

 

선형 회귀의 다중 공선성 문제

 

회귀 분석에서 독립변수들 간 강한 상관 관계가 나타나는 문제

 

• 일반적으로 OLS기반의 회귀 계수는 계산은 입력 Feature의 독립성에 많은 영향을 받음
• Feature 간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해짐.
• 이러한 현상을 다중 공선성 (Multi-Collinearity)문제라고 함
• 일반적으로 상관관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용함 or PCA 차원축소

 

 

입력 Feature 간의 상관관계가 높거나 종속적인 관계라고 판단될 시에는:

 

순서대로

1. LinearRegression 적용

2. Regulation 적용

3. RegressionTree 적용

 

 

 

---

2. 회귀 모델의 성능 평가 지표

 

 

Parameter 넣을 때 (y_test, y_pred) 순서대로 넣어야 함!!

 

 

회귀 평가 지표

 

실제값과 예측값의 차이에 기반한 평가 방법을 사용

 

일반적으로 MAE, RMSE, RMSLE를 많이 사용함

 

 

 

• MAE: Mean Absolute Error, 실제 값과 예측 값의 차이를 절댓값으로 변환해 평균한 것
• MSE: Mean Squared Error, 실제 값과 예측 값의 차이를 제곱해 평균한 것
• MSLE: MSE 전체에 log를 적용한 것, 결정값이 클 수록 오류값도 커지기 때문에 일부 큰 오류값들로 인해 전체 오류값이 커지는 것을 막아줌
• RMSE: Root Mean Squared Error, MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있으므로 MSE에 루트를 씌운 것
• RMSLE: RSME에 log를 적용한 것, 결정값이 클 수록 오류값도 커지기 때문에 일부 큰 오류값들로 인해 전체 오류값이 커지는 것을 막아줌
• $R^{2}$: 분산 기반으로 예측 성능을 평가함, 실제 값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 예측 정확도가 높음

 

 

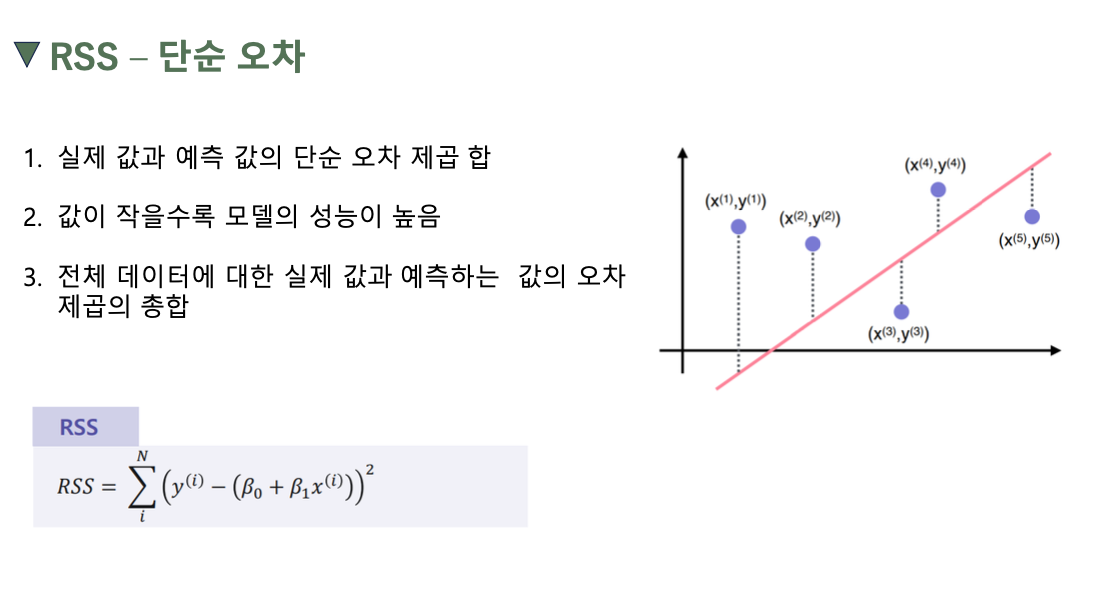
RSS - 단순오차

 

$RSS(w_{0}, w_{1}) = \sum_{i=1}^{N} (y_{i} - (w_{0} + w_{1} * x_{i}))^{2}$

• 가장 간단한 평가 방법으로 직관적인 해석이 가능함
• 그러나 오차를 그대로 이용하기 때문에 입력 값의 크기에 의존적임
• 절대적인 값과 비교가 불가능함

 

 

MSE, MAE - 절대적인 크기에 의존한 지표

 

• MSE(Mean Squared Error)
  • 평균 제곱 오차
  • 실제 값과 예측 값의 오차의 제곱의 평균
  • RSS에서 데이터 수(N)만큼 나눈 값
  • 작을수록 모델의 성능이 높다고 평가할 수 있음

 

• MAE(Mean Absolute Error)
  • 평균 절댓값 오차
  • 실제 값과 예측 값의 오차의 절댓값의 평균
  • 작을수록 모델의 성능이 높다고 평가할 수 있음

 

 

• MSE, MAE 특징
  • MSE: 이상치(Outlier), 데이터들 중 크게 떨어진 값에 민감
  • MAE: 변동성이 큰 지표와 낮은 지표를 같이 예측할 시 유용
  • 가장 간단한 평가 방법들로 직관적인 해석이 가능함
  • 그러나 평균을 그대로 이용하기 때문에 입력 값의 크기에 의존적임
  • 절대적인 값과 비교가 불가능함

 

 

MAE와 RMSE의 비교

 

• MAE에 비해 RMSE는 큰 오류값에 상대적인 페널티를 더 부여함
• 예를 들어 다섯개의 오류 값(실제 값과 예측값의 차이)이 10, 20, 10, 10, 100과 같이 다른 값에 비해 큰 오류값이 존재하는 경우 RMSE는 전반적으로 MAE보다 높음
• $MAE = (10 + 20 + 10 + 10 + 100) / 5 = 30$이고, $RMSE = \sqrt {(100 + 400 + 100 + 100 + 10000)/5} = \sqrt {2140} = 46.26$
• 이처럼 상대적으로 더 큰 오류값이 있을 때 이에 대한 페널티를 더 부과하는 방식 RMSE이다

 

 

$R^{2}$(결정 계수)

 

• 회귀 모델의 설명력을 표현하는 지표
• 1에 가까울수록 높은 성능의 모델이라고 해석할 수 있음

 

$R^{2} = 1 - \frac {RSS} {TSS}$

• RSS: 실제 값과 예측 값 사이의 오차의 제곱
• TSS: 실제 값과 평균 값 사이의 오차의 제곱
• 값이 0일 경우, 데이터의 평균 값을 출력하는 직선 모델을 의미함
• 음수 값이 나올 경우, 평균값 예측보다 성능이 좋지 않음

 

 

 

score 속성 사용시 Paramter 순서 지키기: (X_test, y_test)

 

• Regression Model: model.score(X_test, y_test)로 $R^{2}$ 구현 가능
• Classification Model: model.score(X_test, y_test)로 $Accuracy$ 구현 가능

 

 

 

 

 

 

 

 

RMSLE vs RMSE: RMSLE의 장점 3가지

 

 

1. RMSLE는 Outlier에 강건(Robust)하다

 

• RMSLE는 Outlier가 있더라도 값의 변동폭이 크지 않음
• 매우 큰 Outlier가 추가됐을 경우 RMSE는 크게 증가하지만 RMSLE의 증가는 미미함
• RMSLE는 Outlier에 Robust하다

 

import numpy as np
from sklearn.metrics import mean_squared_error, mean_squared_log_error

y_true = [60, 80, 90]
y_pred = [67, 78, 91]

RMSE = np.sqrt(mean_squared_error(y_true, y_pred))
print("RMSE :", RMSE)

RMSLE = np.sqrt(mean_squared_log_error(y_true, y_pred))
print("RMSLE :", RMSLE)

RMSE : 4.242640687119285
RMSLE : 0.0646679237996832

 

import numpy as np
from sklearn.metrics import mean_squared_error, mean_squared_log_error

y_true = [60, 80, 90, 750]
y_pred = [67, 78, 91, 102]

RMSE = np.sqrt(mean_squared_error(y_true, y_pred))
print("RMSE :", RMSE)

RMSLE = np.sqrt(mean_squared_log_error(y_true, y_pred))
print("RMSLE :", RMSLE)

RMSE : 324.02083266358045
RMSLE : 0.9949158238939428

 

 

2. 상대적 Error를 측정해준다

 

• 예측값과 실제값에 log를 취해주면 로그 공식에 의해 아래와 같이 예측값과 실제값의 상대적 비율을 구할 수 있음
• 값의 절대적 크기가 변하더라도 상대적 크기가 동일하다면 RMSE값은 변하지만 RMSLE 값은 동일
• 다만 금전적인 부분의 예측과 같이 큰 금액을 비슷하게 예측하는 것보다 작은 금액을 큰 차이 없이 예측하는 것이 더 좋게 나옴

 

y_true = [90]
y_pred = [100]

RMSE = np.sqrt(mean_squared_error(y_true, y_pred))
print("RMSE :", RMSE)

RMSLE = np.sqrt(mean_squared_log_error(y_true, y_pred))
print("RMSLE :", RMSLE)

RMSE : 10.0
RMSLE : 0.10426101032440993

y_true = [9000]
y_pred = [10000]

RMSE = np.sqrt(mean_squared_error(y_true, y_pred))
print('RMSE :', RMSE)

RMSLE = np.sqrt(mean_squared_log_error(y_true, y_pred))
print('RMSLE :', RMSLE)

RMSE : 1000.0
RMSLE : 0.10534940571943174

 

 

 

 

3. Under Estimation에 큰 Penalty를 부여한다

 

• 예측값이 실제값보다 작을 때 더 큰 Penalty를 부여함 (Loss function의 Loss가 더 크다)
• 예측값과 실제값의 차이가 같다면 RMSE는 Over Estimation 이나 Under Estimation은 동일하지만 RMSLE는 Under Estimation에 더 큰 Penalty를 부여함

 

y_true = [1000]
y_pred = [600]

RMSE = np.sqrt(mean_squared_error(y_true, y_pred))
print('RMSE :', RMSE)

RMSLE = np.sqrt(mean_squared_log_error(y_true, y_pred))
print('RMSLE :', RMSLE)

RMSE : 400.0
RMSLE : 0.5101598447800129

 

y_true = [1000]
y_pred = [1400]

RMSE = np.sqrt(mean_squared_error(y_true, y_pred))
print('RMSE :', RMSE)

RMSLE = np.sqrt(mean_squared_log_error(y_true, y_pred))
print('RMSLE :', RMSLE)

RMSE : 400.0
RMSLE : 0.3361867670217862

 

 

 

---

3. Scikit - Learn 회귀 평가 API

 

 

 

Scikit - Learn 회귀 평가 API

 

다음은 각 평가 방법에 대한 사이킷런의 API 및 cross_val_score이나 GridSearchCV에서 평가 시 사용되는 scoring 파라미터의 적용 값

 

 

 

MSE를  사용하기 위해서는:

metrics.mean_squared_error(실제값, 예측값, squared=True ) 이용

 

 

RMSE를  사용하기 위해서는:

metrics.mean_squared_error(실제값, 예측값, squared=False )

• 기본 squared가 아니라 root - squared이므로 False값으로 지정

 

 

 

 

Scikit - Learn scoring 함수에 회귀 평가 적용 시 유의사항

 

cross_val_score, GridSearchCV와 같은 Scoring 함수에 회귀 평가 지표를 적용 시 유의사항

 

• MAE의 사이킷런 scoring 파라미터 값은 'neg_mean_absolute_error' 이다. 이는 Negative(음수) 값을 가진다는 의미인데, MAE는 절댓값의 합이기 때문에 음수가 될 수 없음

 

• Scoring 함수에 'neg_mean_absolute_error'를 적용해 음수값을 반환하는 이유는 사이킷런의 Scoring 함수가 score 값이 클수록 좋은 평가 결과로 자동 평가하기 때문임
• 따라서 -1을 원래의 평가 지표 값에 곱해서 음수 (Negative)를 만들어 작은 오류 값이 더 큰 숫자로 인식하게 됨, 예를 들어 10 > 1이지만 음수를 곱하면 -1 > -10이 됨

 

• metrics.mean_absolute_error( )와 같은 사이킷런 평가 지표 API는 정상적으로 양수의 값을 반환하지만 Scoring함수의 scoring 파라미터 값 'neg_mean_absolute_error'가 의미하는 것은 (-1) * metrics.mean_absolute_error( ) 이니 주의가 필요함

 

 

 

 

---

4. LinearRegression Class를 활용한 Boston 주택 가격 예측

 

 

LinearRegression Class

 

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from sklearn.datasets import load_boston
import warnings
warnings.filterwarnings('ignore')  #사이킷런 1.2 부터는 보스턴 주택가격 데이터가 없어진다는 warning 메시지 출력 제거
%matplotlib inline

# boston 데이타셋 로드
boston = load_boston()

# boston 데이타셋 DataFrame 변환 
bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names)

# boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함. 
bostonDF['PRICE'] = boston.target
print('Boston 데이타셋 크기 :',bostonDF.shape)
bostonDF.head()

 

 

각 Feature 설명

 

• CRIM: 지역별 범죄 발생률
• ZN: 25,000평방피트를 초과하는 거주 지역의 비율
• INDUS: 비상업 지역 넓이 비율
• CHAS: 찰스강에 대한 더미 변수(강의 경계에 위치한 경우는 1, 아니면 0)
• NOX: 일산화질소 농도
• RM: 거주할 수 있는 방 개수
• AGE: 1940년 이전에 건축된 소유 주택의 비율
• DIS: 5개 주요 고용센터까지의 가중 거리
• RAD: 고속도로 접근 용이도
• TAX: 10,000달러당 재산세율
• PTRATIO: 지역의 교사와 학생 수 비율
• B: 지역의 흑인 거주 비율
• LSTAT: 하위 계층의 비율
• MEDV: 본인 소유의 주택 가격(중앙값)

 

 

• 각 Column 별로 주택가격에 미치는 영향도를 조사

# 2개의 행과 4개의 열을 가진 subplots를 이용. axs는 4x2개의 ax를 가짐.
fig, axs = plt.subplots(figsize=(16,8) , ncols=4 , nrows=2)
lm_features = ['RM','ZN','INDUS','NOX','AGE','PTRATIO','LSTAT','RAD']
for i , feature in enumerate(lm_features):
    row = int(i/4)
    col = i%4
    # 시본의 regplot을 이용해 산점도와 선형 회귀 직선을 함께 표현
    sns.regplot(x=feature , y='PRICE',data=bostonDF , ax=axs[row][col])

 

 

• 학습과 테스트 데이터 세트로 분리하고 학습/예측/평가 수행

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error , r2_score

y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)

X_train , X_test , y_train , y_test = train_test_split(X_data , y_target ,test_size=0.3, random_state=156)

# Linear Regression OLS로 학습/예측/평가 수행. 
lr = LinearRegression()
lr.fit(X_train ,y_train )
y_preds = lr.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)

print('MSE : {0:.3f} , RMSE : {1:.3F}'.format(mse , rmse))
print('Variance score : {0:.3f}'.format(r2_score(y_test, y_preds)))

# MSE : 17.297 , RMSE : 4.159
# Variance score : 0.757

 

• 가중치 행렬의 각 entry는 각 column과 mapping 시켜야함

print('절편 값:',lr.intercept_)
print('회귀 계수값:', np.round(lr.coef_, 1))

# 절편 값: 40.995595172164315
# 회귀 계수값: [ -0.1   0.1   0.    3.  -19.8   3.4   0.   -1.7   0.4  -0.   -0.9   0.
#   -0.6]

# CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT

 

• 회귀 계수를 큰 값 순으로 정렬하기 위해 Series 생성, index가 column명에 유의

# 회귀 계수를 큰 값 순으로 정렬하기 위해 Series로 생성. index가 컬럼명에 유의
coeff = pd.Series(data=np.round(lr.coef_, 1), index=X_data.columns )
coeff.sort_values(ascending=False)

# RM          3.4
# CHAS        3.0
# RAD         0.4
# ZN          0.1
# INDUS       0.0
# AGE         0.0
# TAX        -0.0
# B           0.0
# CRIM       -0.1
# LSTAT      -0.6
# PTRATIO    -0.9
# DIS        -1.7
# NOX       -19.8
# dtype: float64

 

회귀계수 중 하나만 두드러지게 크다면 Overfitting이 발생할 가능성이 높다

 

• cross_val_score 적용

from sklearn.model_selection import cross_val_score

y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)
lr = LinearRegression()

# cross_val_score( )로 5 Fold 셋으로 MSE 를 구한 뒤 이를 기반으로 다시  RMSE 구함. 
neg_mse_scores = cross_val_score(lr, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores  = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)

# cross_val_score(scoring="neg_mean_squared_error")로 반환된 값은 모두 음수 
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 2))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores, 2))
print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))


#  5 folds 의 개별 Negative MSE scores:  [-12.46 -26.05 -33.07 -80.76 -33.31]
#  5 folds 의 개별 RMSE scores :  [3.53 5.1  5.75 8.99 5.77]
#  5 folds 의 평균 RMSE : 5.829