[Let's AI] 1-6. Numpy

1. 행렬의 곱셈 4가지 관점

• Rank
  
  • 해당 행렬의 Column Space의 dimension
• Column Space
  • 해당 행렬을 구성하는 column vector들이 span 하는 공간
• Span
  • vector들의 선형결합으로 나타낼 수 있는 벡터공간

 

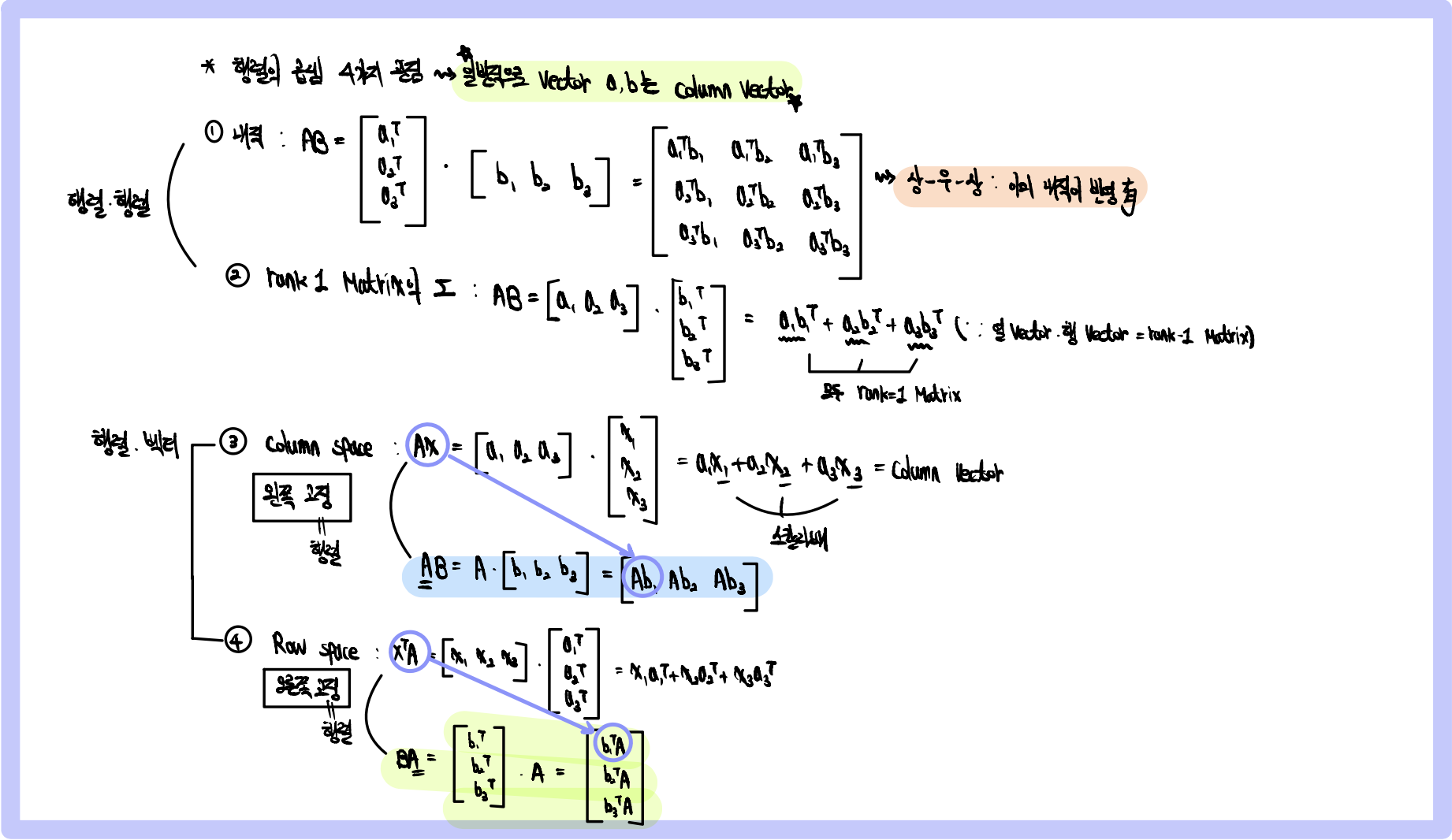
• 행렬의 곱셈 중 Inner product를 이용한 방법:
  • i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬

 

• 행렬의 곱셉 중 Column Space를 이용한 방법  : 

 

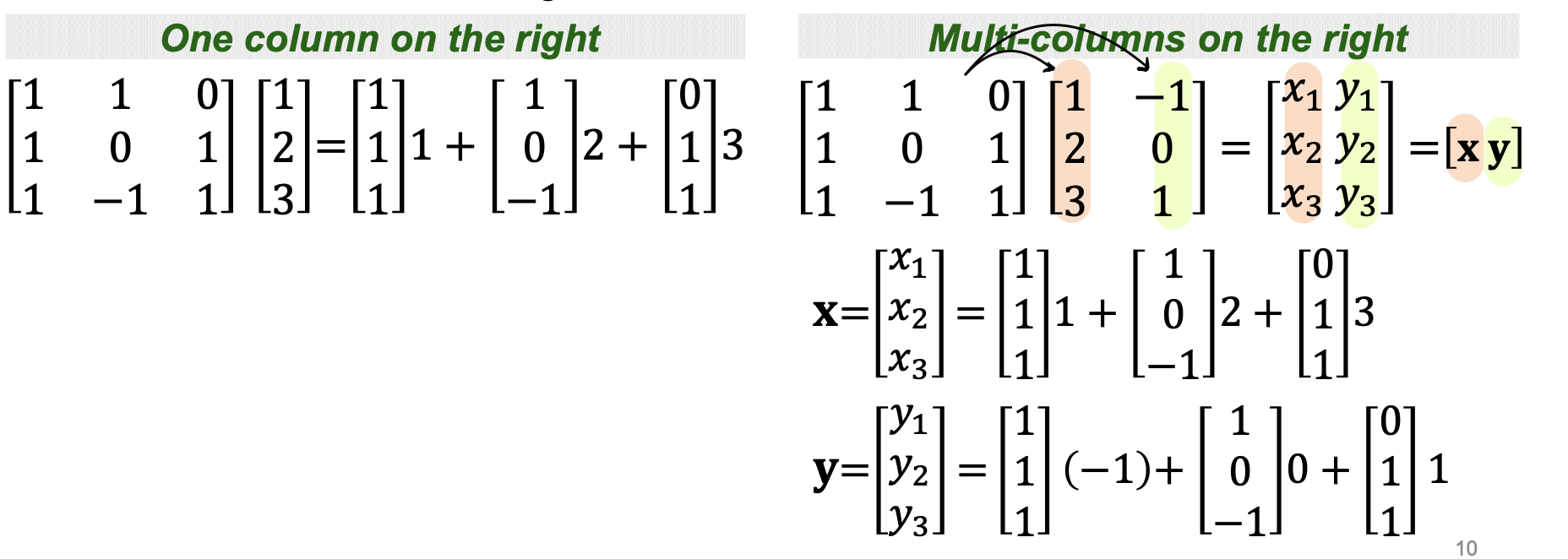
1) 결과 행렬의 column 개수 = 오른쪽 행렬의 column 개수

 

-> 오른쪽 행렬의 column을 하나씩 꺼내서 계산 후 다시 삽입 :

matrix * matrix 연산을 matrix * vector 연산 여러개로 분리

 

2) Matrix * Vector 연산 수행 : 

 

-> 각 vector의 element를 왼쪽 Matrix의 column에 분배해서 합하기 (image 상으로 이해)

 

 

2. Numpy

 

 

 

 

• Numerical Python
• 파이썬의 고성능 과학 계산용 패키지
• Matrix와 Vector와 같은 Array 연산의 사실상의 표준
• 한글로 넘파이로 주로 통칭, 넘피/늄파이라고 부르기도 함

Numpy 특징

• 일반 List에 비해 빠르고, 메모리 효율적
• 반복문 없이 데이터 배열에 대한 처리를 지원함 (for문, list comprehension 없이)
• 선형대수와 관련된 다양한 기능을 제공함
• C, C++, 포트란 등의 언어와 통합 가능

 

3. ndarray

import numpy as np

• numpy의 호출 방법
• 일반적으로 numpy는 np라는 alias(별칭) 이용해서 호출함
• 특별한 이유는 없음 세계적인 약속 같은 것

 

< Array creation >

test_array = np.array([1, 4, 5, 8], float) print(test_array) type(test_array[3])

• Numpy 연산에서 가장 기본이 되는 array :  ndarray (numpy dimesion array)
• numpy는 np.array 함수를 활용하여 배열을 생성함 -> ndarray
• numpy는 하나의 데이터 type만 배열에 넣을 수 있음
• List와 가장 큰 차이점, Dynamic typing not supported
  • 실행시점에 data type을 결정 X : 미리 결정하고 시작
  • 메모리 공간을 어떻게 잡을지 미리 선언

 

• C의 Array를 사용하여 배열을 생성함

 

 

< caution >

• np.array()를 이용해 배열을 만들고 연산을 하는 경우 : 2차원 리스트에서 계산함
• np.array([[1,2],[3,4]])와 같이 ()안에 2차원 리스트를 넣어준다

In [1]:

pip install numpy

 

WARNING: Ignoring invalid distribution -umpy (/Users/eric/opt/anaconda3/lib/python3.9/site-packages)
WARNING: Ignoring invalid distribution -umpy (/Users/eric/opt/anaconda3/lib/python3.9/site-packages)
Requirement already satisfied: numpy in /Users/eric/opt/anaconda3/lib/python3.9/site-packages (1.25.0)
WARNING: Ignoring invalid distribution -umpy (/Users/eric/opt/anaconda3/lib/python3.9/site-packages)
WARNING: Ignoring invalid distribution -umpy (/Users/eric/opt/anaconda3/lib/python3.9/site-packages)
WARNING: Ignoring invalid distribution -umpy (/Users/eric/opt/anaconda3/lib/python3.9/site-packages)
WARNING: Ignoring invalid distribution -umpy (/Users/eric/opt/anaconda3/lib/python3.9/site-packages)
Note: you may need to restart the kernel to use updated packages.

In [2]:

import numpy as np

test_array = np.array([1,2,3,4], float)
print(test_array)
print(type(test_array))

print(test_array[3])
print(type(test_array[3]))    

 

[1. 2. 3. 4.]
<class 'numpy.ndarray'>
4.0
<class 'numpy.float64'>

In [3]:

import numpy as np
test_array = np.array(['1',2,'3',4,5],float)
print(test_array)
print(type(test_array[3]))  
# numpy.float64 : 하나의 데이터가 차지하는 공간이 64bit (메모리 공간의 수정)

 

 

[1. 2. 3. 4. 5.]
<class 'numpy.float64'>

• Python List : 메모리 주소의 위치를 지정
• Numpy array : 값 자체를 지정

 

< Array creation >

 

• shape : numpy array의 object의 dimension 구성을 반환함
  • Array (vector, matrix, tensor)의 크기, 형태 등에 대한 정보
    • vector : row vector로 처리 : (y,) 
    • matrix : 원래 하던대로 x(row) x y(column) 으로 처리 : (x, y)
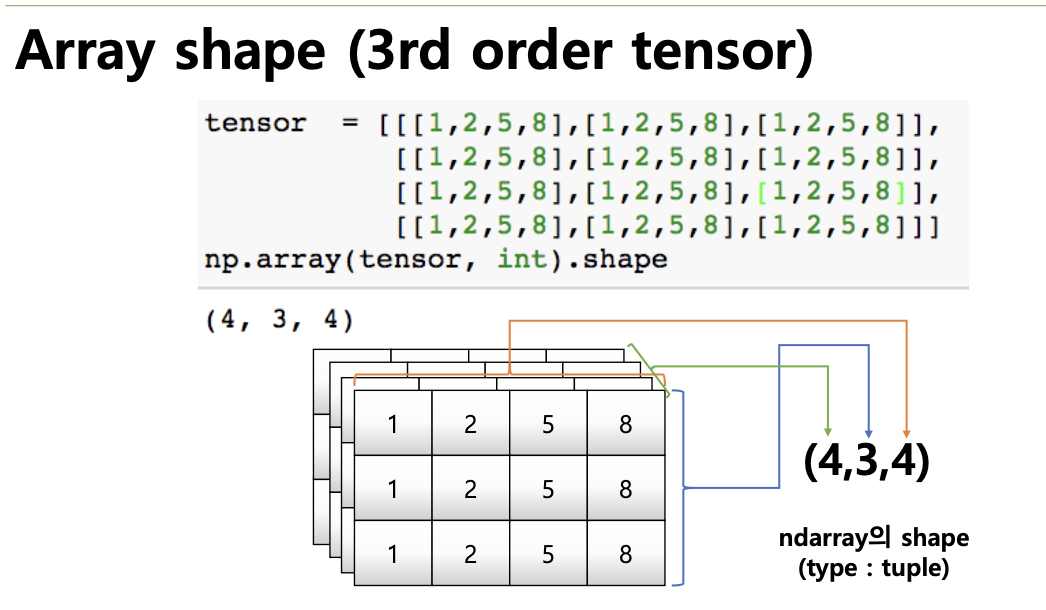
    • 3rd order tensor : 앞에 tensor의 깊이가 따로 들어 감 : (depth, x, y)
      • depth는 기존의 z방향이 아니라 일반적인 직교좌표계에서의 -y 방향을 나타냄
    • rank가 높아질 수록 하나씩 오른쪽으로 밀린다

 

• ndim – number of dimension (rank와 동치) 
• size – total data의 개수 (부피와 비슷) = depth * x * y
• dtype : numpy array의 데이터 type을 반환함
  • Ndarray의 single element가 가지는 data type
  • 각 element가 차지하는 memory의 크기가 결정됨

 

 

• nbytes : ndarray object의 메모리 크기를 반환함 
  • float 32 : 32 bits = 4 bytes -> element 개수 * 4 를 반환
  • float 64 :  64 bits = 8 bytes -> element 개수 * 8 를 반환

 

In [4]:

test_array = np.array([1, 4, 5, "8"], float) # String Type의 데이터를 입력해도
test_array2 = np.array([1,2,3,4], float)


print(test_array)
print(type(test_array[3])) # Float Type으로 자동 형변환을 실시
print(test_array.dtype) # Array(배열) 전체의 데이터 Type을 반환함 
print(test_array.shape) # Array(배열) 의 shape을 반환함
print(test_array2.shape) # Array(배열) 의 shape을 반환함

 

[1. 4. 5. 8.]
<class 'numpy.float64'>
float64
(4,)
(1, 4)

In [5]:

test_array = np.array([[1,2,3],[4.5,5,6]],dtype=int)
test_array2 = np.array([[1,2,3],[4.5,5,6]],dtype=np.float32)
print(test_array)
print(test_array2)

 

[[1 2 3]
 [4 5 6]]
[[1.  2.  3. ]
 [4.5 5.  6. ]]

 

4. Handling Shape

 

< reshape >

• Array의 shape의 크기를 변경함 (element의 갯수는 동일)
• Array의 size만 같다면 다차원으로 자유로이 변형가능
• reshape(depth, x, y)꼴로 reshape가 되고,
• -1은 size를 기반으로 나머지 setting된 숫자들을 기반으로 적절히 결정됨

 

< flatten >

• 다차원 array를 1차원 array로 변환

In [6]:

test_matrix = [[1,2,3,4],[5,6,7,8]]
print(np.array(test_matrix).shape)

new_array = np.array(test_matrix).reshape(4,2)
print(new_array)
new_array = np.array(test_matrix).reshape(-1,4)
print(new_array)
new_array = np.array(test_matrix).flatten()
print(new_array)

 

(2, 4)
[[1 2]
 [3 4]
 [5 6]
 [7 8]]
[[1 2 3 4]
 [5 6 7 8]]
[1 2 3 4 5 6 7 8]

 

5. Indexing & Slicing 

 

< indexing >

• List와 달리 이차원 배열에서 [0,0] 과 같은 표기법을 제공함
• Matrix 일경우 앞은 row 뒤는 column을 의미함
  • [depth][x][y] 으로 해석

In [7]:

a = np.array([[1, 2, 3], [4, 5, 6]], int)
print(a)
print(a[0,0]) # Two dimensional array representation #1 
print(a[0][0]) # Two dimensional array representation #2

a[0,0] = 12 # Matrix 0,0 에 12 할당 print(a)
a[0][0] = 5 # Matrix 0,0 에 12 할당 print(a)
print(a)

 

[[1 2 3]
 [4 5 6]]
1
1
[[5 2 3]
 [4 5 6]]

 

< slicing >

• List와 달리 행과 열 부분을 나눠서 slicing이 가능함
• Matrix의 부분 집합을 추출할 때 유용함
• [ Row, Column ]순 : 컴퓨터식 좌표계로 범위 설정 (-y방향으로 row, +x 방향으로 column)
• [ Row ]순 : 입력받는 값이 하나만 있다면 Row를 의미, Column은 전체로 선택됨

In [8]:

a = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]], int)

print(a[:,2:]) # 전체 Row의 2열 이상
print(a[1,1:3]) # 1 Row의 1열 ~ 2열
print(a[1:3]) # 1 Row ~ 2Row의 전체

 

[[ 3  4  5]
 [ 8  9 10]]
[7 8]
[[ 6  7  8  9 10]]

In [9]:

a = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]],int)

print(a[:,2:])
print(a[2:])
print(a[:,::2])
print(a[::3,::2])

 

[[ 3  4]
 [ 7  8]
 [11 12]
 [15 16]]
[[ 9 10 11 12]
 [13 14 15 16]]
[[ 1  3]
 [ 5  7]
 [ 9 11]
 [13 15]]
[[ 1  3]
 [13 15]]

 

 

 

5. Creation Function

 

 

< arange >

• array의 범위를 지정하여, 값의 list를 생성하는 명령어 : np.arange(start, end, step)
• list의 range와 같은 효과, integer로 0부터 29까지 배열추출
• floating point도 표시가능함

 

In [10]:

a = list(range(30))
print(a)
a = np.arange(30)
print(a)
a = np.arange(0,5,0.5)  # floating point도 표시가능함
print(a)
a = np.arange(30).reshape(5,6)
print(a)
a = np.arange(0, 5, 0.5).tolist() 
# list에서는 소수점 단위로 띄어쓰기는 불가능, numpy에서 처리하고 tolist()
print(a)

 

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25 26 27 28 29]
[0.  0.5 1.  1.5 2.  2.5 3.  3.5 4.  4.5]
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]
 [24 25 26 27 28 29]]
[0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5]

 

< ones, zeros and empty >

• zeros : 0으로 가득찬 ndarray 생성
• np.zeros(shape, dtype, order)
• ones : 1로 가득찬 ndarrary 생성
• np.ones(shape, dtype, order)
• empty : shape만 주어지고 비어있는 ndarray 생성
• (memory initialization이 되지 않음)

• shape = (y) or (y,) : 인수가 1개일 경우 벡터로 생각
• shape = (x,y) : 인수가 2개일 경우 컴퓨터적 좌표계로 생각 (rank = 2)
• shape = (depth, x, y): 인수가 3개일 경우 depth가 앞으로 옴 (rank = 3)

In [11]:

a = np.zeros(shape=(10), dtype=np.int8)  # 10 - zero vector 생성
print(a)
a = np.zeros((2,5)) # 2 by 5 - zero matrix 생성
print(a)

a = np.ones(shape=(5,2))
print(a)
a = np.ones(shape=(2,5), dtype=np.int32)
print(a)

b = np.empty(shape=(10,),dtype=np.int8)
print(b)

c = np.empty(shape=(3,5))
print(c)

 

[0 0 0 0 0 0 0 0 0 0]
[[0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]]
[[1. 1.]
 [1. 1.]
 [1. 1.]
 [1. 1.]
 [1. 1.]]
[[1 1 1 1 1]
 [1 1 1 1 1]]
[1 1 1 1 1 1 1 1 1 1]
[[0.         0.         0.4472136  0.0531494  0.18257419]
 [0.4472136  0.2125976  0.36514837 0.4472136  0.4783446 ]
 [0.54772256 0.4472136  0.85039041 0.73029674 0.4472136 ]]

 

< something_like >

• 기존 ndarray의 shape 크기 만큼 1, 0 또는 empty array를 반환
  • np.ones_like(test_matrix) : 기존 shape을 유지한채 element를 전부 1로 변환
  • np.zeros_like(test_matrix) : 기존 shape을 유지한채 element를 전부 0로 변환
  • np.empty_like(test_matrix) : 기존 shape을 유지한채 element를 전부 empty로 변환

< identity >

• 단위 행렬(i 행렬)을 생성함 : np.identity(test_matrix, dtype)

< eye >

• 대각선의 성분을 전부 1로 처리함 : 대각행렬 만들기
• 대각선인 1인 행렬, k값(시작하는 x좌표)의 시작 index의 변경이 가능

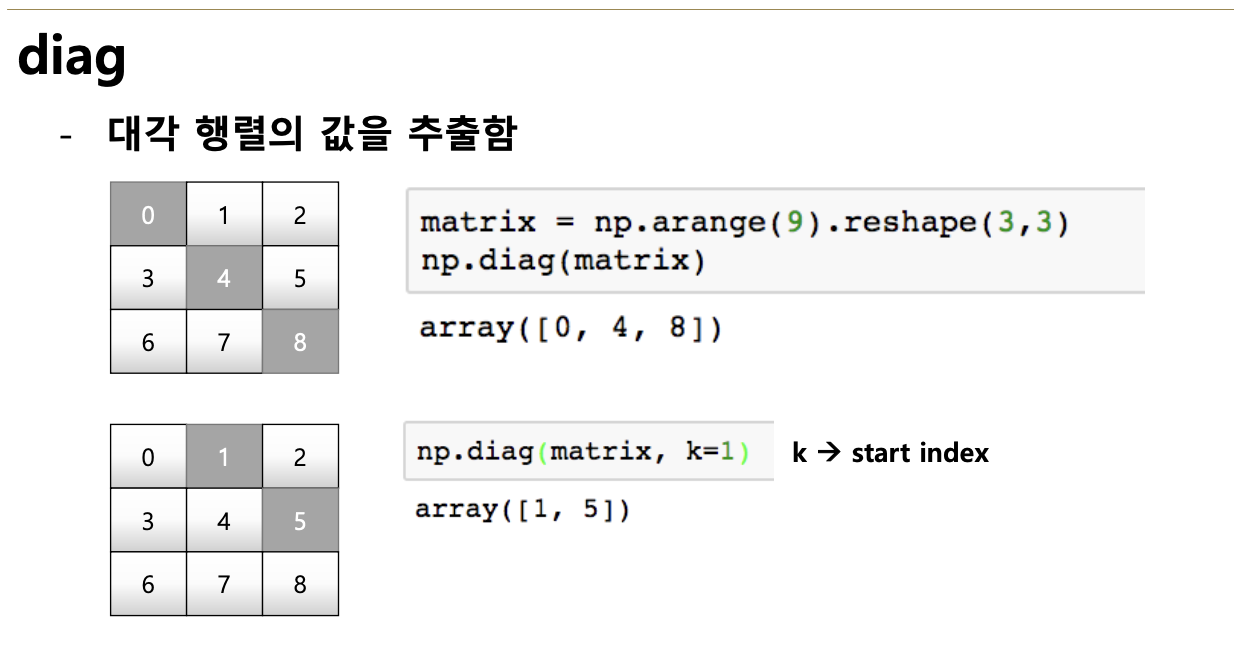
< diag >

• 대각 행렬의 값을 추출함
• k값(시작하는 x좌표)의 시작 index의 변경이 가능

< random sampling >

• 데이터 분포에 따른 sampling으로 array를 생성 

  

In [12]:

test_matrix = np.arange(30).reshape(5,6)
print(np.ones_like(test_matrix))

test_matrix = np.identity(n=3, dtype=np.int8)
print(test_matrix)

np.identity(5,dtype =np.int8)

np.eye(5)
np.eye(N=3, M=5, dtype=np.int8)
np.eye(N=3, M=5, k=2, dtype=np.int8)

matrix = np.arange(30).reshape(5,6)
print(matrix)
np.diag(matrix, k =2)

 

[[1 1 1 1 1 1]
 [1 1 1 1 1 1]
 [1 1 1 1 1 1]
 [1 1 1 1 1 1]
 [1 1 1 1 1 1]]
[[1 0 0]
 [0 1 0]
 [0 0 1]]
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]
 [24 25 26 27 28 29]]

Out[12]:

array([ 2,  9, 16, 23])

In [13]:

print(np.random.uniform(0,1,10).reshape(2,5))   # 균등분포
print(np.random.normal(0,1,10).reshape(2,5))    # 정규분포

 

[[0.7555059  0.95619095 0.02452103 0.56010719 0.13882819]
 [0.97538914 0.79786874 0.29514181 0.88486399 0.26031217]]
[[ 0.18135994 -0.92792528  1.28996436 -0.2604757   0.13966642]
 [ 0.05843369  0.66411765 -0.87248476 -2.29638112 -1.01420041]]

 

 

6. Operation Function

< sum >

• ndarray의 element들 간의 합을 구함, list의 sum 기능과 동일
• 각 축마다 계산한 합을 원소로 하는 새로운 matrix를 생성

< axis >

• 모든 operation function을 실행할 때, 기준이 되는 dimension 축
• 컴퓨터적 사고 기준 : x축 <-> axis = 0 , y축 <-> axis = 1
• 새롭게 생기는 shape의 axis가 0이 된다 : depth (axis=0), x(axis=1), y(axis=2)

In [14]:

import numpy as np

test_array = np.arange(1,11)
print(test_array)
print(test_array.sum(dtype=np.float64))

test_array = np.arange(1,13).reshape(3,4)

print(test_array)
print(test_array.sum(axis=1))
print(test_array.sum(axis=0))

 

[ 1  2  3  4  5  6  7  8  9 10]
55.0
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
[10 26 42]
[15 18 21 24]

 

< 평균 & 표준편차 >

mean & std

• ndarray의 element들 간의 평균 또는 표준 편차를 반환

In [15]:

test_array = np.arange(1,13).reshape(3,4)
print(test_array)

print(test_array.mean())
print(test_array.mean(axis=0, dtype=int))

print(test_array.std())
print(test_array.std(axis = 0, dtype = float))

 

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
6.5
[5 6 7 8]
3.452052529534663
[3.26598632 3.26598632 3.26598632 3.26598632]

 

< concatenate > : 병합 (string처럼)

• Numpy array를 합치는 함수
• vstack : 위아래로 합침 (y방향) / vertical stack
• concatenate with axis = 0 : 위아래로 합침 (y방향)
• hstack : 좌우로 합침 (x방향) / horizonal stack
• concatenate with axis = 1 : 위아래로 합침 (x방향)

Caution! : vstack이나 hstack을 사용할 경우 ()괄호를 두 번 이상 써야함

 

In [16]:

a = np.array([1,2,3])
b = np.array([2,3,4])

print(np.vstack((a,b)))
print(np.hstack((a,b)))

c = np.array([1,2,3]).reshape(3,1)
d = np.array([2,3,4]).reshape(3,1)

print(np.vstack((c,d)))
print(np.hstack((c,d)))

c = np.array([[1], [2], [3]])
d = np.array([[2], [3], [4]])

print(np.vstack((c,d)))
print(np.hstack((c,d)))

 

[[1 2 3]
 [2 3 4]]
[1 2 3 2 3 4]
[[1]
 [2]
 [3]
 [2]
 [3]
 [4]]
[[1 2]
 [2 3]
 [3 4]]
[[1]
 [2]
 [3]
 [2]
 [3]
 [4]]
[[1 2]
 [2 3]
 [3 4]]

In [17]:

a = np.array([[1,2,3]])
b = np.array([[2,3,4]])

c = np.array([[1,2],[3,4]])
d = np.array([[5,6]])

print(np.concatenate((a,b),axis=0))
print(np.concatenate((c,d.T),axis=1))

 

[[1 2 3]
 [2 3 4]]
[[1 2 5]
 [3 4 6]]

 

< array operations b/t arrays >

• Numpy는 array간의 기본적인 사칙 연산을 지원함 
  • 같은 위치에 있는 element 끼리 +/-

In [18]:

test_a = np.array([[1,2,3],[4,5,6]], int)
print(test_a + test_a)
print(test_a - test_a)
print(test_a * test_a)

 

[[ 2  4  6]
 [ 8 10 12]]
[[0 0 0]
 [0 0 0]]
[[ 1  4  9]
 [16 25 36]]

 

< Element-wise operations : 아다마르 곱(*) >

• Array간 shape이 같을 때 일어나는 연산 : * 연산
• 각 element끼리 (같은 위치에 ㅇ)

 

In [19]:

matrix_a = np.arange(1,13).reshape(3,4)

print(matrix_a * matrix_a)

 

[[  1   4   9  16]
 [ 25  36  49  64]
 [ 81 100 121 144]]

 

< Dot product >

< 일반 행렬곱 (@, dot) >

• Matrix의 기본 연산 : @ 연산
• dot 함수 사용 : .dot 연산

< 내적 (np.inner) >

• np.inner 연산

In [20]:

test_a = np.arange(1,7).reshape(2,3)
test_b = np.arange(7,13).reshape(3,2)

print(test_a.dot(test_b))   # @ 연산 = 일반 행렬곱
print(test_a @ test_b)  # .dot 연산 = 일반 행렬곱
print(np.inner(test_a, test_b.T))   # np.inner연산 = 내적 = 전치후 일반 행렬곱

 

[[ 58  64]
 [139 154]]
[[ 58  64]
 [139 154]]
[[ 58  64]
 [139 154]]

 

< transpose >

• transpose 또는 T attribute 사용 -> array.transpose() or array.T

In [21]:

test_a = np.arange(1,7).reshape(2,3)
print(test_a)

print(test_a.T)
print(test_a.transpose())
print(test_a.T.dot(test_a))

 

[[1 2 3]
 [4 5 6]]
[[1 4]
 [2 5]
 [3 6]]
[[1 4]
 [2 5]
 [3 6]]
[[17 22 27]
 [22 29 36]
 [27 36 45]]

 

< broadcasting >

• Shape이 다른 배열 간 연산을 지원하는 기능
• Scalar - vector / vector - matrix / scalar - matrix 간의 연산 모두 지원

In [22]:

test_matrix = np.array([[1,2,3],[4,5,6]], float)
scalar = 3

# matrix - scalar 덧셈
print(test_matrix + scalar)

# matrix - scalar 뺄셈
print(test_matrix - scalar)

# matrix - scalar 곱셈
print(test_matrix * scalar)

# matrix - scalar 나눗셈
print(test_matrix / scalar)

# matrix - scalar 몫
print(test_matrix // scalar)

# matrix - scalar 제곱
print(test_matrix ** scalar)

 

[[4. 5. 6.]
 [7. 8. 9.]]
[[-2. -1.  0.]
 [ 1.  2.  3.]]
[[ 3.  6.  9.]
 [12. 15. 18.]]
[[0.33333333 0.66666667 1.        ]
 [1.33333333 1.66666667 2.        ]]
[[0. 0. 1.]
 [1. 1. 2.]]
[[  1.   8.  27.]
 [ 64. 125. 216.]]

 

< Numpy performance #1 >

• timeit: jupyter 환경에서 코드의 퍼포먼스를 체크하는 함수
• concatenation : 속도가 느려짐

 

In [23]:

def sclar_vector_product(scalar, vector): 
    result = []
    for value in vector: 
        result.append(scalar * value)
        
    return result 

iternation_max = 10000

vector = list(range(iternation_max)) 
scalar = 2

%timeit sclar_vector_product(scalar, vector) # for loop을 이용한 성능
%timeit [scalar * value for value in range(iternation_max)] # list comprehension을 이용한 성능 
%timeit np.arange(iternation_max) * scalar # numpy를 이용한 성능

 

1.07 ms ± 78.3 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
862 µs ± 16.3 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
11.4 µs ± 40.6 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

 

< Numpy performance #2 >

• 일반적으로 속도는 아래 순 for loop < list comprehension < numpy
• 100,000,000번의 loop이 돌 때 약4배이상의 성능차이를 보임
• Numpy는 C로 구현되어 있어, 성능을 확보하는 대신 파이썬의 가장 큰 특징인 dynamic typing을 포기함
• 대용량 계산에서는 가장 흔히 사용됨
• Concatenate 처럼 계산이 아닌, 할당에서는 연산 속도의 이점이 없음

 

< All & Any >

• Array의 데이터 전부(and) 또는 일부(or)가 조건에 만족 여부 반환
  • a> 5  : a의 모든 원소에 대해 comparison이 일어나 일종의 broadcasting으로 볼 수 있음
• any -> 하나라도 조건에 만족한다면 true
• all -> 모두가 조건에 만족한다면 true
• np.logical_and (a > 0, a < 3) : and 조건의 condition
• np.logical_not (b) : not 조건의 condition
• np.logical_or (b,c) : or 조건의 condition

< Comparison operation >

• Numpy는 배열의 크기가 동일 할 때, element간 비교의 결과를 Boolean type으로 반환하여 돌려줌

< np.where >

1) 조건을 만족하는 Index값 반환 : -> where(condition)

2) 조건을 만족할 때 True parameter의 값 반환 / 만족하지 않을 때 False parameter의 값 반환 :

-> where(conidition, True, False)

• np.isnan() : Not a Number 
• np.isfinite() : is finite number

In [24]:

a = np.arange(10)
a

Out[24]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [25]:

a<0

Out[25]:

array([False, False, False, False, False, False, False, False, False,
       False])

In [26]:

np.any(a>5), np.any(a<0)

Out[26]:

(True, False)

In [27]:

np.all(a>5), np.all(a<10)

Out[27]:

(False, True)

In [28]:

a = np.array([1, 3, 0], float)
np.where(a>0, 3, 2)

Out[28]:

array([3, 3, 2])

In [29]:

np.where(a>0)

Out[29]:

(array([0, 1]),)

In [30]:

a = np.array([1, np.NaN, np.Inf], float)
np.isnan(a)

Out[30]:

array([False,  True, False])

In [31]:

np.isfinite(a)

Out[31]:

array([ True, False, False])

 

< argmax & argmin >

• array내 최대값 또는 최소값의 index를 반환함
• axis 기반의 반환

In [32]:

a = np.array([1,2,4,5,8,78,23,3])
np.argmax(a), np.argmin(a)

Out[32]:

(5, 0)

In [33]:

a = np.array([[1,2,4,7],[9,88,6,45],[9,76,3,4]])
np.argmax(a, axis=1), np.argmax(a, axis=0)

Out[33]:

(array([3, 1, 1]), array([1, 1, 1, 1]))

 

< boolean index >

• array의 [index]에 condition(boolean 조건)을 넣는 경우 filter로서 작용함
• True인 index가 아니라 value를 반환함
• numpy는 배열은 특정 조건에 따른 값을 배열 형태로 추출할 수 있음
•  Comparison operation 함수들도 모두 사용가능
• condition에 해당하는 원소만 뽑을 때 : 조건이 True인 index의 element만 추출

 

• Where : 특정 condition에 해당하는 index를 반환
• Boolean index : 특정 condition에 해당하는 value를 반환

 

< fancy index > : a[b], a.take(b)

• numpy는 array(b)를 index value로 사용해서 값을 추출하는 방법
• Matrix 형태의 데이터도 가능
• 단, b는 반드시 모든 원소가 int여야 함 : 정수로 선언 -> a[b] : b를 index로 인식해서 b의 각 원소(인덱스)마다 a의 값을 반환 -> a.take(b) : bracket index와 같은 효과
• a[b,c] : b를 row index, c를 column index로 변환하여 처리 가능

In [34]:

test_array = np.array([1,4,0,2,3,8,9,7], float)
test_array > 3

Out[34]:

array([False,  True, False, False, False,  True,  True,  True])

In [35]:

test_array[test_array >3]

Out[35]:

array([4., 8., 9., 7.])

In [36]:

condition = test_array < 3
test_array[condition]

Out[36]:

array([1., 0., 2.])

In [37]:

a = np.array([2,4,6,8], float)
b = np.array([0,0,1,3,2,1], int)    # 반드시 integer로 선언
a[b]    # b배열의 값을 index로 하여 a의 값들을 추출함

Out[37]:

array([2., 2., 4., 8., 6., 4.])

In [38]:

a.take(b)   # take 함수 : bracket index와 같은 효과

Out[38]:

array([2., 2., 4., 8., 6., 4.])

In [39]:

a = np.array([[1,4],[9,16]], float)
b = np.array([0,0,1,1,0], int)
c = np.array([0,1,1,1,1], int)
a[b,c]  # b를 row index, c를 column index로 변환하여 표시함

Out[39]:

array([ 1.,  4., 16., 16.,  4.])

In [ ]: