[Python ML Guide] Section 1.2: Numpy

https://www.inflearn.com/course/%ED%8C%8C%EC%9D%B4%EC%8D%AC-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EC%99%84%EB%B2%BD%EA%B0%80%EC%9D%B4%EB%93%9C

[개정판] 파이썬 머신러닝 완벽 가이드 - 인프런 | 강의

 

 

---

0. Jupyter Notebook & Intro

 

대표적인 대화형 파이썬 툴

• 프로그래밍과 이에 대한 설명적인 요소를 결합했다는 의미
• 전체 프로그램에서 특정 코드 영역별로 개별 수행을 지원하므로 영역별로 코드 이해가 매우 명확하게 설명될 수 있음
• Notebook, 즉 '공책'이라는 단어에서 유추할 수 있듯이 중요 코드 단위로 설명을 적고 코드를 수행해 그 결과를 볼 수 있게 만듦
• 직관적으로 어떤 코드가 어떤 역할을 하는지 매우 쉽게 이해할 수 있도록 지원

 

---

Numpy와  Pandas의 중요성

 

• 머신러닝 어플리케이션 구현에서 데이터의 추출/가공/변환이 상당한 영역을 차지하고 데이터 처리 부분은 대부분 넘파이와 판다스의 몫
• 사이킷런이 넘파이 기반에서 작성됐기 때문에 넘파이의 기본 프레임워크를 이해하지 못하면 사이킷런 역시 실제 구현에서 많은 벽에 부딪힐 수 있음
• 사이킷런은 API 구성이 매우 간결하고 직관적이어서 이를 이용한 개발 또한 상대적으로 쉽지만 넘파이와 판다스 API는 더 방대하기 때문에 이를 익히는데 시간이 많이 소모될 수 있음. 하지만 머신러닝을 위해서 이들을 많은 시간을 들여 전문적으로 공부하는 것은 효율적이지 못함
• 넘파이와 판다스에 대한 기본 프레임워크와 중요 API만 습독하고, 일단 코드와 부딪쳐 가면서 모르는 API에 대해서는 인터넷 자료를 통해 체득하는 것이 머신러닝 뿐만 아니라 넘파이와 판다스에 관한 이해를 넓히는게 더 빠른 방법임

 

---

1. Numpy

 

Numerical Python

Python의 고성능 과학 계산용 Package이며, Matrix 혹은 Vector와 같은 array 연산의 사실상의 표준

 

• 일반 list에 비해 빠르고, memory 효율적
• 반복문(for, list comprehension) 없이 데이터 배열에 대한 처리를 지원함
• 선형대수와 관련된 다양한 기능을 제공함
• C, C++, 포트란 등의 언어와 통합 가능

 

import numpy as np

 

• numpy의 일반적 호출방법
• 일반적으로 numpy는 np라는 alias(별칭)을 이용해서 호출함
• 특별한 이유는 없음, 세계적인 약속과 같은 것

---

2. ndarray & Array Creation

 

ndarray

• Numpy dimension array
• Numpy 연산에서 가장 기본이 되는 array
• ndarray내의 데이터값은 숫자값, 문자열 값, 불 값 등이 모두 가능
• 숫자형의 경우 int형(8/16/32 bit), unsigned int형(8/16/32 bit), float형(16/32/64/128 bit) 그리고 이보다 더 큰 숫자 값이나 정밀도를 위해 complex 타입도 제공
• ndarray 내의 data type은 그 연산의 특성상 같은 data type만 가능

 

ndarray - axis

• axis 0, 1, 2: rank가 높아질수록 하나씩 뒤로 밀린다 (+1)
• 새로 들어온 축이 axis 0이 되고 기존의 축들에 +1 부과
• axis 단위로 차원이 부여됨

 

 

 

astype()

• ndarray의 data type 변환
• 변경을 원하는 타입을 astype()에 인자로 입력
• 대용량 데이터를 ndarray로 만들 때 메모리를 절약하기 위해 자주 사용
• 0,1,2와 같이 크지 않은 범위의 숫자를 위해서 64bit float형 보다는 8bit 혹은 16bit의 integer형으로 변환하는 것이 메모리를 더 절약하게 됨
• 대용량 데이터를 다룰 때 메모리 절약을 위해 형변환을 특히 고려해야 한다
• float -> int로 변환시 '버림'이 일어난다

 

new_array.astype('int32')

# array([1, 2, 3, 4, 5], dtype=int32)

new_array.astype(np.int32)

# array([1, 2, 3, 4, 5], dtype=int32)

array_int = np.array([1, 2, 3])
array_float = array_int.astype(np.float64)
print(array_float, array_float.dtype)

array_int1 = array_float.astype("int32")
print(array_int1, array_int1.dtype)

array_float1 = np.array([1.1, 2.2, 3.3])
array_int2 = array_float1.astype('int32')
print(array_int2, array_int2.dtype)

# [1. 2. 3.] float64
# [1 2 3] int32
# [1 2 3] int32

 

Array Creation = np.array(list, dtype)

• numpy는 np.array 함수를 활용하여 배열을 생성함: ndarray
• numpy는 하나의 data type만 배열에 넣을 수 있음
• list와 가장 큰 차이점: dynamic typing not supported
  • 실행시점에 data type을 결정 X, 미리 결정하고 시작
  • 메모리 공간을 어떻게 잡을지 미리 선언
• C의 array를 사용하여 배열을 생성
• 다른 data type이 섞여 있는 list를 ndarray로 변경하면 데이터 크기가 더 큰 데이터 타입으로 형 변환을 일괄 적용함

 

array = np.array([1,2,3,4.5])
array

# array([1. , 2. , 3. , 4.5])

type(array[1])

# numpy.float64
# 하나의 데이터가 차지하는 공간이 64bit (메모리 공간의 수정)

 

array = np.array([1,2,3, 'test'])
array

# array(['1', '2', '3', 'test'], dtype='<U21')

 

array = np.array([1,2,3,'test', 4.5])
array

# array(['1', '2', '3', 'test', '4.5'], dtype='<U32')

 

Python List vs Numpy Array

• Python List : 메모리 주소의 위치를 지정
• Numpy array : 값 자체를 지정

 

 

---

3. Shape

 

shape

• numpy array의 dimension 구성을 반환
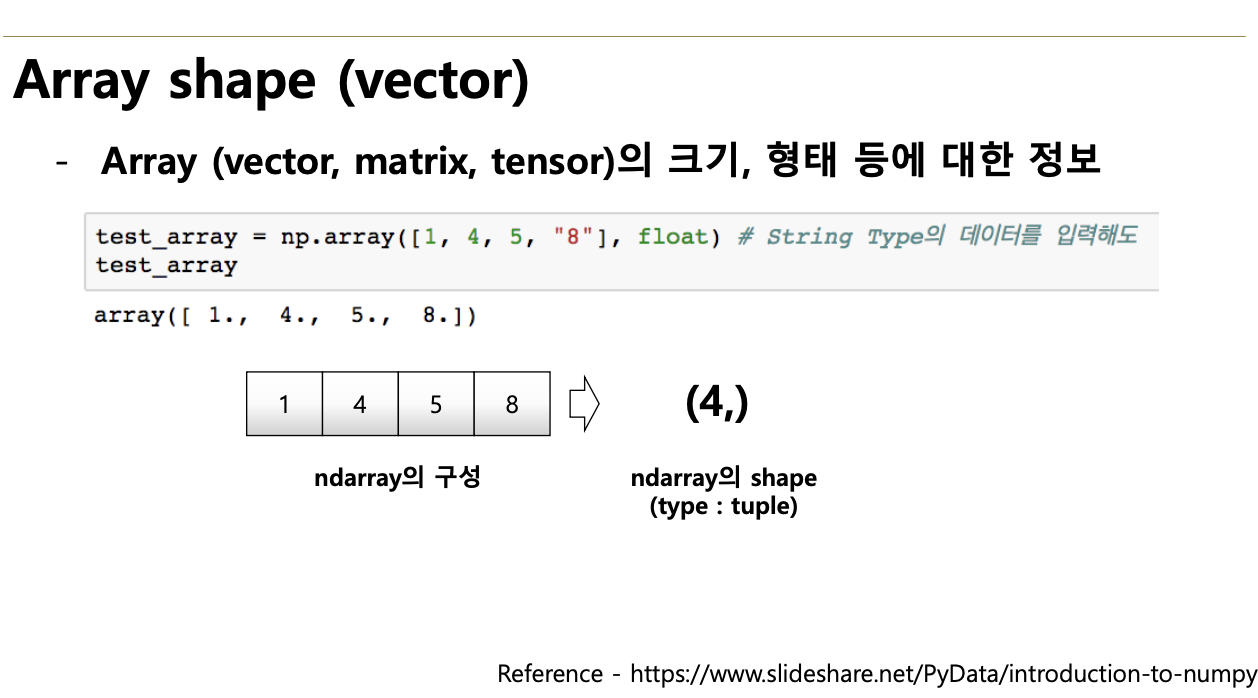
• Array(vector, matrix, tensor)의 크기, 형태 등에 대한 정보
• vector: (y,)
• matrix: (x,y) 
  • x: row, y: column 개수로 처리
• tensor: (depth, x, y)
  • depth는 직교좌표계에서의 x(+-)축 방향이라고 생각하면 편하다
  • yz 평면(shape = (x,y)) 을 depth만큼 쌓았다고 생각
• rank가 높아질수록 하나씩 오른쪽으로 밀린다 (y가 계속 오른쪽으로 밀리는 것처럼)

 

Caution!

• np.array()를 이용하여 배열을 만들고 연산을 하는 경우: 2차원 리스트에서 계산함 (shape도 2차원이어야 함)
• np.array([[1,2]])와 같이 () 안에 2차원 리스트를 넣어준다: [ [ ] ]와 같이 2개 필요

 

list1 = [1, 2, 3]
print("list type:", type(list1))
array1 = np.array(list1)
print("array1 type:", type(array1))
print("array1 array 형태:", array1.shape)

array2 = np.array([[1, 2, 3], [2, 3, 4]])
print("array2 type:", type(array2))
print("array2 array 형태:", array2.shape)

array3 = np.array([[1, 2, 3]])
print("array3 type:", type(array3))
print("array3 array 형태:", array3.shape)


# list type: <class 'list'>
# array1 type: <class 'numpy.ndarray'>
# array1 array 형태: (3,)
# array2 type: <class 'numpy.ndarray'>
# array2 array 형태: (2, 3)
# array3 type: <class 'numpy.ndarray'>
# array3 array 형태: (1, 3)

 

 

 

rank

• rank A = dim col A
• Matrix의 Column Space의 dimension

Column Space

• Matrix를 구성하는 column vector들이 span 하는 공간

Span

• vector들의 선형결합으로 나타낼 수 있는 vector space

 

 

 

ndim

• number of dimensions (rank와 동일)

print(f"array1: {array1.ndim}차원, array2: {array2.ndim}차원, array3: {array3.ndim}차원")

# array1: 1차원, array2: 2차원, array3: 2차원

 

size

• total data(element)의 개수 = $depth \times x \times y$

 

dtype

• numpy array의 data type을 반환
• ndarray의 single element가 가지는 data type
• 각 element가 차지하는 memory의 크기가 결정됨
• 'int32'와 같이 string으로 작성하거나 np.int32와 같이 method으로 작성

 

list1 = [1,2,3]
print(type(list1))
array1 = np.array(list1)
print(type(array1))
print(array1, array1.dtype)

# <class 'list'>
# <class 'numpy.ndarray'>
# [1 2 3] int64

list2 = [1,2,'test']
array2 = np.array(list2)
print(array2, array2.dtype)

list3 = [1,2,3.0]
array3 = np.array(list3)
print(array3, array3.dtype)

# ['1' '2' 'test'] <U21
# [1. 2. 3.] float64

 

nbytes 

• ndarray object의 메모리 크기를 반환함 
• float 32 : 32 bits = 4 bytes -> element 개수 * 4 를 반환
• float 64 :  64 bits = 8 bytes -> element 개수 * 8 를 반환

 

---

4. Handling Shape

 

reshape(depth, x, y)

• ndarray를 특정 차원 및 형태로 변환, 변환 형태를 함수 인자로 부여하면 됨
• array의 shape의 크기를 변경함 (element의 개수는 동일)
• array의 size만 같다면 다차원으로 자유로이 변형가능
• -1은 size를 유지한채 나머지 setting된 숫자들을 기반으로 적절히 변형됨
• 인자에 -1을 부여하면 -1에 해당하는 axis의 크기는 가변적이되 -1이 아닌 인자값에 해당하는 axis 크기는 인자값으로 고정되어 ndarray의 shape를 반환

 

array1 = np.arange(10)
print(array1)

array2 = array1.reshape(-1, 5)
print("array2 shape:", array2.shape)

array3 = array1.reshape(5, -1)
print("array3 shape:", array3.shape)

# [0 1 2 3 4 5 6 7 8 9]
# array2 shape: (2, 5)
# array3 shape: (5, 2)

 

 

 

reshape(-1,1) vs reshape(-1,) 

• reshape(-1,1): 2차원으로 변환하되 column axis 크기가 1로 고정
• reshape(-1,): flatten()과 동일, 1차원으로 변환
• reshape(-1,1) or reshape(-1,)과 같은 형식으로 변환이 요구되는 경우가 많음
• 주로 머신러닝 API의 인자로 1차원 ndarray를 명확하게 2차원 ndarray로 변환하여 입력하기를 원하거나
• 반대의 경우 reshape()을 이용하여 ndarray의 형태를 변환시켜  주는데 사용함

 

array1 = np.arange(8)
array3d = array1.reshape(2, 2, 2)
print("array3d:", array3d.tolist(), sep="\n")

# 3차원 ndarray를 2차원 ndarray로 변환하되 column 개수=1
array5 = array3d.reshape(-1, 1)
print("array5:", array5.tolist(), sep="\n")
print("array5 shape:", array5.shape)

# 1차원 ndarray를 2차원 ndarray로 변환하되 column 개수=1
array6 = array1.reshape(-1, 1)
print("array6:", array6.tolist(), sep="\n")
print("array6 shape:", array6.shape)

# array3d:
# [[[0, 1], [2, 3]], [[4, 5], [6, 7]]]
# array5:
# [[0], [1], [2], [3], [4], [5], [6], [7]]
# array5 shape: (8, 1)
# array6:
# [[0], [1], [2], [3], [4], [5], [6], [7]]
# array6 shape: (8, 1)

# column 개수 = 1
print(array5)

# column 개수 = 1
print(array5.tolist())

# [[0]
#  [1]
#  [2]
#  [3]
#  [4]
#  [5]
#  [6]
#  [7]]

# [[0], [1], [2], [3], [4], [5], [6], [7]]

 

 

flatten()

• 다차원 array를 1차원 array로 변환

 

# 3차원 array를 1차원으로 변환

print(array3d.reshape(-1,))
print(array3d.flatten())

# [0 1 2 3 4 5 6 7]
# [0 1 2 3 4 5 6 7]

 

---

5. Creation Function

 

arange(start, stop, step)

• array의 범위를 지정하여, 값의 list를 생성하는 명령어 
• list의 range와 같은 효과, start부터 stop-1까지 배열추출
• floating point도 표시가능함

sequence_array = np.arange(10)
print(sequence_array)
print(sequence_array.dtype, sequence_array.shape)

# [0 1 2 3 4 5 6 7 8 9]
# int64 (10,)

 

ones, zeros, empty(shape, dtype, order)

• ones: 1로 가득찬 ndarray 생성
• zeros: 0으로 가득찬 ndarray 생성
• empty: shape만 주어지고 비어있는 ndarray 생성
  • memory initialization이 되지 않음

 

# (3,2) shape을 가지는 모든 원소가 0, dtype은 int32인 ndarray 생성
zero_array = np.zeros((3, 2), dtype=np.int32)
print(zero_array)
print(zero_array.dtype, zero_array.shape)

# (3,2) shape을 가지는 모든 원소가 1인 ndarray 생성
one_array = np.ones((3, 2))
print(one_array)
print(one_array.dtype, one_array.shape)

# [[0 0]
#  [0 0]
#  [0 0]]
# int32 (3, 2)
# [[1. 1.]
#  [1. 1.]
#  [1. 1.]]
# float64 (3, 2)

 

something_like(matrix)

• 기존 ndarray의 shape 크기 만큼 1, 0 또는 empty array를 반환
• ones_like: 기존 shape을 유지한채 element를 전부 1로 변환
• zeros_like: 기존 shape을 유지한채 element를 전부 0으로 변환
• empty_like: 기존 shape을 유지한채 element를 전부 empty로 변환

 

identity(matrix, dtype)

• 단위 행렬(identity matrix)을 생성함

 

eye(row, column, k)

• 대각선의 성분이 전부 1이고 나머지가 0인 행렬 생성 : 대각행렬 만들기
• k = 대각선의 시작 x좌표: 1이 시작하는 index(위치)를 바꿀 수 있음

 

diag(matrix, k)

• 대각 행렬의 값을 추출함
• k값(시작하는 x좌표)의 시작 index 변경이 가능

 

random sampling = np.random.distribution(start, end, # of elements)

• 데이터 분포에 따른 sampling으로 array를 생성

 

---

6. Indexing & Slicing

 

indexing 유형

• 특정 위치의 단일값 추출
  • 원하는 위치의 인덱스 값을 지정하면 해당 위치의 데이터가 반환
• 슬라이싱 (Slicing)
  • 연속된 인덱스상의 ndarray를 추출하는 방식
  • [start:end]으로 표시하면 start ~ (end-1) 까지의 index에 해당하는 ndarray를 반환
• 펜시 인덱싱 (Fancy Indexing)
  • 일정한 인덱싱 집합을 리스트 또는 ndarray 형태로 지정해 해당 위치에 있는 ndarray를 반환
• 불린 인덱싱 (Boolean Indexing)
  • 특정 조건에 해당하는지 여부인 True/False 값 인덱싱 집합을 기반으로 True에 해당하는 인덱스 위치에 있는 ndarray를 반환

 

 

indexing (특정 위치의 단일값 추출)

• List와 달리 이차원 배열에서 [x, y] or [x][y] 방법 두 가지 다 제공함
• 3차원일 경우 [depth][x][y]로 해석

 

 

# 1부터 9까지의 1차원 ndarray 생성
array1 = np.arange(1, 10)
print("array1: ", array1)

# index는 0부터 시작하므로 array1[2]는 3번째 index 위치의 data 값을 의미
value = array1[2]
print("value", value)
print(type(value))

# array1:  [1 2 3 4 5 6 7 8 9]
# value 3
# <class 'numpy.int64'>

print("맨 뒤의 값:", array1[-1], ", 맨 뒤에서 두번째 값:", array1[-2])

# 맨 뒤의 값: 9 , 맨 뒤에서 두번째 값: 8

array1[0] = 9
array1[8] = 0
print("array1:", array1)

# array1: [9 2 3 4 5 6 7 8 0]

array1d = np.arange(1, 10)
array2d = array1d.reshape(3, 3)
print(array2d)

print("(row=0, col=0) index 가리키는 값:", array2d[0, 0])
print("(row=0, col=1) index 가리키는 값:", array2d[0, 1])
print("(row=2, col=0) index 가리키는 값:", array2d[1, 0])
print("(row=3, col=2) index 가리키는 값:", array2d[2, 2])

# [[1 2 3]
#  [4 5 6]
#  [7 8 9]]
# (row=0, col=0) index 가리키는 값: 1
# (row=0, col=1) index 가리키는 값: 2
# (row=2, col=0) index 가리키는 값: 4
# (row=3, col=2) index 가리키는 값: 9

 

 

slicing

• List와 달리 행과 열 부분을 나눠서 slicing이 가능함
• Matrix의 부분 집합을 추출할 때 유용함
• [ x 범위, y 범위 ]: 각각 Row, Column 지정 범위만큼 부분추출
• [ x 범위 ]: 단독으로 있으면 x범위만 select하고 y범위는 전체

 

 

 

 

arrya1 = np.arange(1,10)
# 위치 인덱스 0~2까지 추출
array4 = array1[1:3]
print(array4)

# 위치 인덱스 3부터 마지막까지 추출
array5 = array1[3:]
print(array5)

# 위치 인덱스로 전체 데이터 추출
array6 = array1[:]
print(array6)

# [2 3]
# [4 5 6 7 8 9]
# [1 2 3 4 5 6 7 8 9]

array1d = np.arange(1, 10)
array2d = array1d.reshape(3, 3)
print("array2d: \n", array2d)

print("array2d[0:2, 0:2] \n", array2d[0:2, 0:2])
print("array2d[1:3, 0:3] \n", array2d[1:3, 0:3])
print("array2d[1:3, :] \n", array2d[1:3, :])
print("array2d[:, :] \n", array2d[:, :])
print("array2d[:2, 1:] \n", array2d[:2, 1:])
print("array2d[0:2, 0] \n", array2d[0:2, 0])

# array2d: 
#  [[1 2 3]
#  [4 5 6]
#  [7 8 9]]
# array2d[0:2, 0:2] 
#  [[1 2]
#  [4 5]]
# array2d[1:3, 0:3] 
#  [[4 5 6]
#  [7 8 9]]
# array2d[1:3, :] 
#  [[4 5 6]
#  [7 8 9]]
# array2d[:, :] 
#  [[1 2 3]
#  [4 5 6]
#  [7 8 9]]
# array2d[:2, 1:] 
#  [[2 3]
#  [5 6]]
# array2d[0:2, 0] 
#  [1 4]

print(array2d[0])
print(array2d[1])
print('array2d[0] shape:', array2d[0].shape, 'array2d[1] shape:', array2d[1].shape)

# [1 2 3]
# [4 5 6]
# array2d[0] shape: (3,) array2d[1] shape: (3,)

 

 

Fancy Indexing

• 특정한 index를 가진 인덱싱 집합을 리스트 또는 ndarray 형태로 지정해 해당 위치에 있는 ndarray를 반환
• list나 ndarray로 인덱싱 집합을 지정하면 해당 위치에 해당하는 ndarray를 반환하는 인덱싱 방식
• Matrix[ Fancy Index ] = Matrix[ index 집합 using list or ndarray ] 
• Matrix [ [x값 Fancy Index] , [y값 Fancy Index] ]

 

 

 

array1d = np.arange(1, 10)
array2d = array1d.reshape(3, 3)
print(array2d)

array3 = array2d[[0, 1], 2]
print("array2d[[0, 1], 2] => ", array3.tolist())

array4 = array2d[[0, 1], 0:2]
print("array2d[[0, 1], 0:2] => ", array4.tolist())

array5 = array2d[[0, 1]]
print("array2d[[0, 1]] => ", array5.tolist())


# [[1 2 3]
#  [4 5 6]
#  [7 8 9]]
# array2d[[0, 1], 2] =>  [3, 6]
# array2d[[0, 1], 0:2] =>  [[1, 2], [4, 5]]
# array2d[[0, 1]] =>  [[1, 2, 3], [4, 5, 6]]

 

 

Boolean Indexing

• 특정 조건에 해당하는지 여부인 True/False 값 인덱싱 집합을 기반으로 True에 해당하는 인덱스 위치에 있는 ndarray를 반환
• 조건 condition 필터링과 추출을 동시에 할 수 있기 때문에 매우 자주 사용되는 인덱싱 방식
• Matrix[ Boolean Index ]

 

 

 

 

array1d = np.arange(1, 10)
print(array1d)
# [ ] 안에 array1d > 5 Boolean indexing을 적용

array3 = array1d[array1d > 5]
print('array1d > 5 Boolean Indexing 결과 값 :', array3)

# [1 2 3 4 5 6 7 8 9]
# array1d > 5 Boolean Indexing 결과 값 : [6 7 8 9]

val = array1d > 5
print(val, type(val), val.shape)

# [False False False False False  True  True  True  True] <class 'numpy.ndarray'> (9,)

boolean_indexes = np.array([False, False, False, False, False,  True,  True,  True,  True])
array3 = array1d[boolean_indexes]
print('Boolean Index으로 flitering 결과 :', array3)

# Boolean Index으로 flitering 결과 : [6 7 8 9]

 

---

7. Operation Functions

 

 

 

np.unique(ndarray, return_counts=True)

• ndarray의 원소를 중복 제거하여 ndarray로 반환
• Pandas의 value_counts()와 동일하게 기능
• return_counts=True일 경우
  • unique, counts로 unpacking
  •  unique는 원소의 중복을 제거한 ndarray로, counts는 각 원소의 개수를 원소로 가진 ndarray로 반환

 

# y target 값의 분포를 확인
unique, counts = np.unique(y, return_counts=True)
print(unique,counts)

[0 1 2] [67 67 66]

 

 

 

sum(dtype, axis)

• ndarray의 element들 간의 합을 구함
• list의 sum기능과 동일
• 각 축마다 계산한 합을 원소로 하는 새로운 matrix를 생성

 

test_array = np.arange(1, 11)
print(test_array)
print(test_array.sum(dtype=np.float64))

test_array = np.arange(1, 13).reshape(3, 4)

print(test_array)
print(test_array.sum(axis=1))
print(test_array.sum(axis=0))

# [ 1  2  3  4  5  6  7  8  9 10]
# 55.0
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
# [10 26 42]
# [15 18 21 24

 

mean(axis, dtype) & std(axis, dtype)

• ndarray의 element들 간의 평균 혹은 표준편차를 반환

 

test_array = np.arange(1, 13).reshape(3, 4)
print(test_array)

print(test_array.mean())
print(test_array.mean(axis=0, dtype=int))

print(test_array.std())
print(test_array.std(axis=0, dtype=float))

# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
# 6.5
# [5 6 7 8]
# 3.452052529534663
# [3.26598632 3.26598632 3.26598632 3.26598632]

 

 

Mathematical Functions

• 그 외에도 다양한 수학 연산자를 제공함 (np.something 호출)

 

 

concatenate

• Numpy array를 합치는 함수: 각 인자가 2차원 Data 형태여야 함
• 위아래로 합치는 경우 (y방향)
  • vstack(vertical stack)
  • concatenate with axis = 0
• 좌우로 합치는 경우 (x방향)
  • hstack(horizonal stack)
  • concatenate with axis = 1
• Caution!
  • vstack or hstack 사용시 ()괄호를 두 번 이상 써야함

a = np.array([1, 2, 3])
b = np.array([2, 3, 4])

print(np.vstack((a, b)))
print(np.hstack((a, b)))

c = np.array([1, 2, 3]).reshape(3, 1)
d = np.array([2, 3, 4]).reshape(3, 1)

print(np.vstack((c, d)))
print(np.hstack((c, d)))

c = np.array([[1], [2], [3]])
d = np.array([[2], [3], [4]])

print(np.vstack((c, d)))
print(np.hstack((c, d)))

# [[1 2 3]
#  [2 3 4]]
# [1 2 3 2 3 4]
# [[1]
#  [2]
#  [3]
#  [2]
#  [3]
#  [4]]
# [[1 2]
#  [2 3]
#  [3 4]]
# [[1]
#  [2]
#  [3]
#  [2]
#  [3]
#  [4]]
# [[1 2]
#  [2 3]
#  [3 4]]

a = np.array([[1,2,3]])
b = np.array([[2,3,4]])

c = np.array([[1,2],[3,4]])
d = np.array([[5,6]])

print(np.concatenate((a,b),axis=0))
print(np.concatenate((c,d.T),axis=1))

# [[1 2 3]
#  [2 3 4]]
# [[1 2 5]
#  [3 4 6]]

 

---

8. Array Operations

 

Operations b/w arrays

• Numpy는 array 간의 기본적인 사칙 연산을 지원함
• 같은 위치에 있는 element 끼리 +/-

 

Numpy Array 곱연산

 

• 스칼라곱(*)
  • [n,m] * [n,m] = [n,m]
  • Array간 shape이 같을 때 or Broadcasting 가능
  • 각 행렬의 원소끼리의 곱을 성분으로 갖는 행렬을 반환
  • Broadcasting 가능: Matrix * (column, row) Vector ONLY
    • [1,m] * [n,m] = [n,m] 
    • [m,1] * [m,n] = [m,n]
    • [m,n] * [m,1] = [m,n]
    • [n,m] * [1,m] = [n,m]

• 내적(dot)
  • Inner Product: $u \cdot v = u^{T}v$
  • [n,m].dot([m,k]) = [m,k]
  • np.dot([n,m], [m,k]) = [m,k]

• 행렬곱 (@)
  • i번째 행벡터와 j번째 열벡터의 내적을 성분으로 갖는 행렬을 반환
  • 2차원에서는 .dot() & @는 동일한 기능
  • 3차원에서는 텐서곱(외적)을 하게 되어 내적과 달라짐
  • [n,m] @ [m,k] = [m,k]

 

np.dot(A, B)

[참고자료] https://jimmy-ai.tistory.com/75

[Numpy] 파이썬 내적, 행렬곱 함수 np.dot() 사용법 총정리

 

• 1차원 X 1차원: 벡터 내적 (element-wise 방식으로 각 원소를 곱한 값들을 더한 내적 연산)
  • 수식 : 보통 열벡터로 처리 (column vector) 
  • 코드 : 보통 행벡터로 처리 (row vector)
  • Column vector로 들어오면 Transpose해서 Row vector로 처리

 

• 2차원 X 2차원: 행렬 곱 (@ 사용을 권장)

 

• N차원 X 스칼라: 단순 스칼라배 연산 (* 사용을 권장, np.dot 사용하지 말 것)

 

• N차원 X 1차원
  • 왼쪽이 N차원인 경우 각 행마다 오른쪽의 벡터와 내적을 수행
  • 오른쪽이 N차원이면 각 열마다 왼쪽의 벡터와 내적을 수행

 

• N차원 X M차원
  • 왼쪽 array의 각 행, 오른쪽 array의 각 열끼리 순서대로 내적을 수행한 결과를 반환

 

 

 

Caution!!

• 행렬연산을 하기 위해서는 2차원 리스트가 필요함 : [ [ ] ]으로 []를 2번 넣어준다

 

a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[7, 8], [9, 10], [11, 12]])

dot_product = a.dot(b)
dot_product2 = np.dot(a, b)
print("행렬 내적 결과: ", dot_product, dot_product2, sep="\n")

dot_product3 = a @ b
print("행렬 곱 결과: ", dot_product3, sep="\n")

inner_product = np.inner(a, b.T)
print("np.inner 결과: ", inner_product, sep="\n")

# 행렬 내적 결과: 
# [[ 58  64]
#  [139 154]]
# [[ 58  64]
#  [139 154]]
# 행렬 곱 결과: 
# [[ 58  64]
#  [139 154]]
# np.inner 결과: 
# [[ 58  64]
#  [139 154]]

 

np.inner

• i번째 행벡터와 j번째 행벡터의 내적을 성분으로 갖는 행렬을 반환
• 수학에서는 말하는 내적과는 다르다!
• $np.inner(u,v) = uv^{T}$이지만 수학에서는 $u \cdot v = u^{T}v이다!
• np.inner([n,m], [k,m])

 

 

Transpose

• $(A)_{ij} = (A)^{T} _{ji}$
• array.transpose() or array.T 

a = np.array([[1, 2], [3, 4]])
transpose_a = a.transpose()
print("A의 전치행렬: \n", transpose_a)

# A의 전치행렬:
#  [[1 3]
#  [2 4]]

 

sort()

• np.sort(ndarray): 인자로 들어온 원 행렬은 그대로 유지한 채 원 행렬의 정렬된 행렬을 반환
• ndarray.sort(): 원 행렬 자체를 정렬한 형태로 변환하며 반환값은 None
• 기본적으로 오름차순으로 행렬 내 원소를 정렬, 내림차순으로 정렬하기 위해서는 끝에 [::-1]으로 처리

org_array = np.array([3, 1, 9, 5])
print("원본 배열:", org_array)

# np.sort()로 정렬
sort_array1 = np.sort(org_array)
print("np.sort() 호출 후 반환된 정렬 배열 ", sort_array1)
print("np.sort() 호출 후 원본 배열:", org_array)

# ndarray.sort()로 정렬
sort_array2 = org_array.sort()
print("ndarray.sort() 호출 후 반환된 정렬 배열 ", sort_array2)
print("ndarray.sort() 호출 후 원본 배열:", org_array)

# 원본 배열: [3 1 9 5]
# np.sort() 호출 후 반환된 정렬 배열  [1 3 5 9]
# np.sort() 호출 후 원본 배열: [3 1 9 5]
# ndarray.sort() 호출 후 반환된 정렬 배열  None
# ndarray.sort() 호출 후 원본 배열: [1 3 5 9]

sort_array1_desc = np.sort(org_array)[::-1]
print("내림차순으로 정렬:", sort_array1_desc)

# 내림차순으로 정렬: [9 5 3 1]

 

 

array2d = np.array([[8, 12], [7, 1]])

sort_array2d_axis0 = np.sort(array2d, axis=0)
print("axis 0으로 정렬: \n", sort_array2d_axis0)

sort_array2d_axis1 = np.sort(array2d, axis=1)
print("axis 1으로 정렬: \n", sort_array2d_axis1)

# axis 0으로 정렬:
#  [[ 7  1]
#  [ 8 12]]
# axis 1으로 정렬:
#  [[ 8 12]
#  [ 1  7]]

 

 

argsort()

• 원본 행렬 정렬 시 정렬된 행렬의 원래 인덱스를 필요로 할 때 (key mapping시) ng.argsort()를 이용함
• np.argsort()는 정렬 행렬의 원본 index를 ndarray형으로 반환

 

org_array = np.array([3, 1, 9, 5])
sort_indices = np.argsort(org_array)
print(type(sort_indices))
print("행렬 정렬 시 원본 배열의 인덱스:", sort_indices)

# <class 'numpy.ndarray'>
# 행렬 정렬 시 원본 배열의 인덱스: [1 0 3 2]

org_array = np.array([3, 1, 9, 5])
sort_indices_desc = np.argsort(org_array)[::-1]
print("행렬 내림차순 정렬시 원본 배열의 인덱스:", sort_indices_desc)

# 행렬 내림차순 정렬시 원본 배열의 인덱스: [2 3 0 1]

name_array = np.array(["John", "Mike", "Sarah", "Kate", "Samuel"])
score_array = np.array([78, 95, 84, 98, 88])

sort_indices_asc = np.argsort(score_array)
print("성적 오름차순 정렬 시 score_array의 index:", sort_indices_asc)
print("성적 오름차순으로 name_array의 이름 출력:", name_array[sort_indices_asc])

# 성적 오름차순 정렬 시 score_array의 index: [0 2 4 1 3]
# 성적 오름차순으로 name_array의 이름 출력: ['John' 'Sarah' 'Samuel' 'Mike' 'Kate']

 

Broadcasting

• shape 다른 배열간 연산을 지원하는 기능
• Scalar - vector, vector - matrix, scalar - matrix 간의 연산 모두 지원

test_matrix = np.array([[1, 2, 3], [4, 5, 6]], float)
scalar = 3

# matrix - scalar 덧셈
print(test_matrix + scalar)

# matrix - scalar 뺄셈
print(test_matrix - scalar)

# matrix - scalar 곱셈
print(test_matrix * scalar)

# matrix - scalar 나눗셈
print(test_matrix / scalar)

# matrix - scalar 몫
print(test_matrix // scalar)

# matrix - scalar 제곱
print(test_matrix**scalar)


# [[4. 5. 6.]
#  [7. 8. 9.]]
# [[-2. -1.  0.]
#  [ 1.  2.  3.]]
# [[ 3.  6.  9.]
#  [12. 15. 18.]]
# [[0.33333333 0.66666667 1.        ]
#  [1.33333333 1.66666667 2.        ]]
# [[0. 0. 1.]
#  [1. 1. 2.]]
# [[  1.   8.  27.]
#  [ 64. 125. 216.]]

 

 

Numpy Performance

• timeit: jupyter 환경에서 코드의 퍼포먼스를 체크하는 함수
• concatenation : 속도가 느려짐

def sclar_vector_product(scalar, vector): 
    result = []
    for value in vector: 
        result.append(scalar * value)
        
    return result 

iternation_max = 10000

vector = list(range(iternation_max)) 
scalar = 2

%timeit sclar_vector_product(scalar, vector) # for loop을 이용한 성능
%timeit [scalar * value for value in range(iternation_max)] # list comprehension을 이용한 성능 
%timeit np.arange(iternation_max) * scalar # numpy를 이용한 성능

# 932 µs ± 19.4 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
# 839 µs ± 66.6 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
# 11.6 µs ± 833 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

 

• 일반적으로 속도는 아래 순 for loop < list comprehension < numpy
• 100,000,000번의 loop이 돌 때 약4배이상의 성능차이를 보임
• Numpy는 C로 구현되어 있어, 성능을 확보하는 대신 파이썬의 가장 큰 특징인 dynamic typing을 포기함
• 대용량 계산에서는 가장 흔히 사용됨
• Concatenate 처럼 계산이 아닌, 할당에서는 연산 속도의 이점이 없음

 

---

9. Comparisons

 

 

All & Any

• array의 데이터 전부(and) 또는 일부(or)가 조건에 만족 여부 반환
  • a> 5  : a의 모든 원소에 대해 comparison이 일어나 일종의 broadcasting으로 볼 수 있음
• any -> 하나라도 조건에 만족한다면 true
• all -> 모두가 조건에 만족한다면 true

 

 

Comparison operation

• Numpy는 배열의 크기가 동일 할 때, element간 비교의 결과를 Boolean type으로 반환하여 돌려줌
• np.logical_and (a > 0, a < 3) : and 조건의 condition
• np.logical_not (b): not 조건의 condition
• np.logical_or (b,c): or 조건의 condition

 

 

np.where

• 조건을 만족하는 Index값 반환 
  •  where(condition)
• 조건을 만족할 때 True parameter의 값 반환 / 만족하지 않을 때 False parameter의 값 반환 :
  • where(conidition, True, False)

 

np.where vs Boolean Index

• Where : 특정 condition에 해당하는 index를 반환
• Boolean index : 특정 condition에 해당하는 value를 반환

 

argmax & argmin

• array내 최대값 또는 최소값의 index를 반환함
• axis 기반의 반환

a = np.array([1, 2, 4, 5, 8, 78, 23, 3])
np.argmax(a), np.argmin(a)

# (5, 0)

a = np.array([[1, 2, 4, 7], [9, 88, 6, 45], [9, 76, 3, 4]])
np.argmax(a, axis=1), np.argmax(a, axis=0)

# (array([3, 1, 1]), array([1, 1, 1, 1]))

 

---

10. numpy data i/o

 

loadtxt & savetxt

• Text type의 데이터를 읽고, 저장하는 기능

 

numpy object  - npy

• Numpy object (pickle) 형태로 데이터를 저장하고 불러옴
• Binary 파일 형태로 저장

 

---

11. Summary

 

• 넘파이는 파이썬 머신러닝을 구성하는 핵심 기반으로 반드시 이해가 필요함
• 넘파이 API는 매우 넓은 범위를 다루고 있으므로 머신러닝 애플리케이션을 작성할 때 중요하게 활용될 수 있는 핵심 개념 위주로 숙지하는 것이 좋음
• 넘파이는 판다스에 비해 친절한 API를 제공하지 않음. 2차원의 데이터라면 데이터 가공을 위해 넘파이 보다는 판다스를 이용하는 것이 보다 효율적임