728x90
1. Classification
- Hyperplane을 기준으로 score 값을 계산하여 classification을 수행
- Hyperplane을 구성하는 model parameter가 w이면 w vector는 hyperplane에 수직인 방향으로 생성

- 여러 개의 Hyper Plane을 그을 수 있음
- 서로 다른 종류의 Hyper Plane은 서로 다른 성능을 제공할 수 있음

- Hyper Plane을 $W_{1}$ 로 잡으면 positive sample들 근처에서 또 다른 positive sample이 나타날 가능성이 높음
- Hyper Plane을 $W_{3}$로 잡으면 negative sample들 근처에서 또 다른 negative sample이 나타날 가능성이 높음
- 즉, 각 Hyper Plane들에서 오류가 나타날 가능성이 높다


- Positive sample과 negative sample 중간 어딘가에 hyper plane을 긋는 것이 최적이다

2. SVM: Support Vector Machine
- Margin
- Hyperplane ~ Support Vector 사이의 거리 $\times 2$

- Support Vector
- positive sample들 중 hyper plane과 가장 가까운 sample (vector)
- negative sample들 중 hyper plane과 가장 가까운 sample (vector)
- 성능을 결정짓는 가장 민감한 Data Point
- support vector들 사이의 margin을 Maximize
- Outlier들에 대해서도 안정적인 성능을 제공해야함

- Model Parameter $w$ vector : Hyperplane에 수직인 방향
- Margin을 최소화하기 위해 다양한 Optimization을 사용
- $\left|h_{w b}(x) \right| = projection\: length \times \left\| w \right\|$ 에서 Projection Length = Distance


3. SVM Optimization
- Hard margin SVM
- sample들이 linearly separable하다고 가정
- support vector들 사이의 영역 margin에서는 어떠한 sample들도 존재하지 않는다는 뜻
- Soft margin SVM
- 어느정도의 error는 용인한다 : margin 영역에서 일부 sample들이 나올 수 있음
- Nonlinear Trasform & Kernel Trick
- SVM이 linear separable한 hyperplane만 사용가능하다는 제약을 극복하기 위해 사용
- 2차원의 sample들을 high-dimension sample들로 mapping을 하는 함수를 사용

4. Hard Margin SVM

- Margin $\frac{2}{\left\|w \right\|}$를 maximize
- = $\left\|w \right\|$를 minimize
- = $\left\|w^{2} \right\|$를 minimize
- Constrained Optimization Problem
- Decision Variables: 의사결정변수
- Objective Function: 목적함수
- Constraints: 제약식
- Parameters: 상수(Const)
- Lagrangian Cost 도입
- Constrained Optimization -> Unconstrained Optimization + Dual Problem

6. Soft Margin SVM & Kernel Trick
- sample들이 linearly separable 하지 않는다면 : hyperplane으로 sample들을 구분할 수 없다


- Kernel Function 이용
- linearly separable 하지 않은 data sample들이 있다고 할 때
- Kernel Function을 이용하여 Dimension을 높여서 linearly separable하게 만드는 과정

- 자주 사용하는 Kernel Functions
- 각 함수마다 고유한 parameter가 존재하기 때문에 유저가 선택해야 함
- polynomial
- Gaussian radial basis function (RBF)
- Hyperbolic tangent (multiplayer perceptron kernel)


7. ANN (Artificial Neural Network)
- Nonlinear Classification Model을 제공
- Deep Neural Network의 기본이 됨
- 인간의 뇌 신경을 모사한 형태로 모델이 구성
- Computer Vision, Image recognition 등의 최근 연구에 많이 활용
- 신경망: linear model에 activation function(비선형함수)을 합성

- Activation Functions (활성함수)
- sigmoid
- z값이 극단적으로 갈 수록 gradient값이 작아지면서 학습량이 줄어듦
- tanh
- RELU
- 미분을 해도 gradient = 1로 일정
- 최근에 ANN에서 가장 많이 활용
- sigmoid

- DNN
- ANN에 계층을 깊게 쌓으면 DNN이 형성
- 각각의 계층에 따라서 학습을 하게 되는 feature의 형태가 달라지게 됨
- nonlinear 함수들이 계층적으로 쌓여가면서 signal spade에서의 복잡한 신호들의 패턴을 더 정확하게 분류가능

- XOR 문제
- 서로 다르면 1, 같으면 0을 출력하는 Gate
- 어떠한 직선을 긋더라도 positive sample(1), negative sample(0)끼리 분류하는 건 어려움

- Multilayer Perceptron
- neural network를 여러 개의 층으로 쌓은 것
- XOR Problem 해결 가능

- How to solve XOR?





- MNIST Data Recognition
- image patch가 들어왔을 때, 각 patch를 0~9까지의 숫자로 classification하는 문제
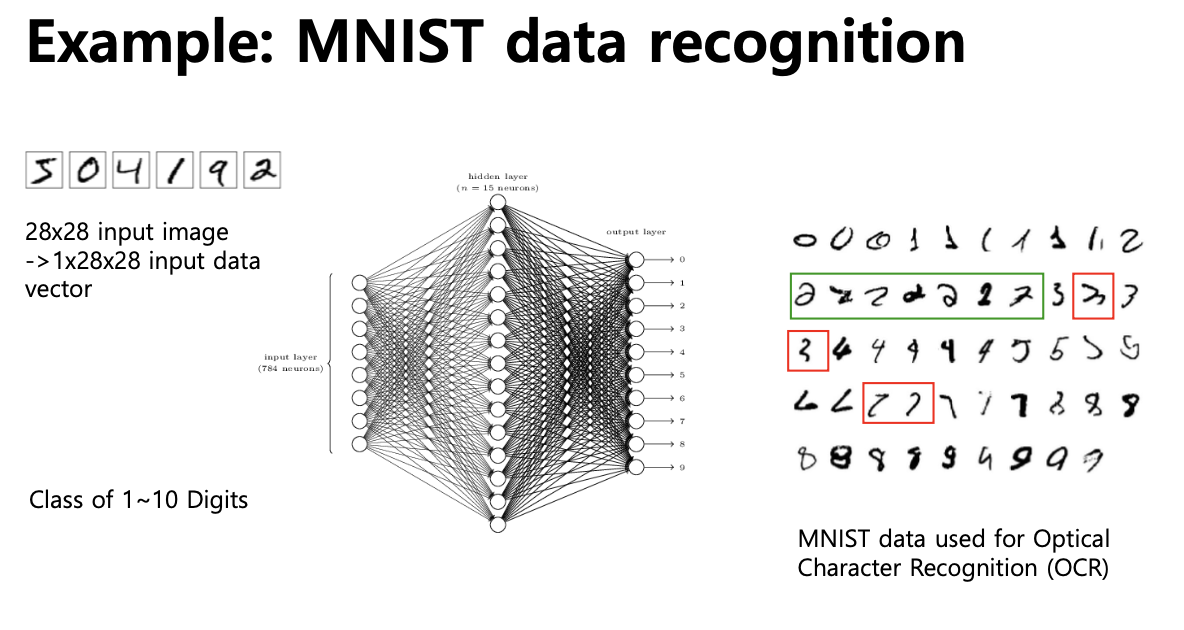
- Gradient Vanishing Problem
- model accuracy가 model의 계층을 늘리더라도 어느 순간 낮아지게 됨
- 학습 parameter를 chain rule을 통해 학습
- 계층이 깊어질수록 gradient값이 줄어듦
- 깊은 layer에 대해서는 학습이 효과적으로 진행되지 않음

- Back Propagation에서 발생하는 문제(gradient vanishing)들을 해결하기 위한 Solution
- pre-training + fine-tuning
- CNN와 같은 Deep learning model로 발전






728x90
