해당 블로그 포스트의 내용은 [한빛미디어]의 '혼자 공부하는 컴퓨터 구조와 운영체제' 책의 저자이신 강민철님께서 강의하신 내용을 위주로 정리했습니다.
https://youtube.com/playlist?list=PLVsNizTWUw7FCS83JhC1vflK8OcLRG0Hl&si=H1U9OoqlmQ8ZiZai
[컴퓨터 공학 기초 강의] 혼자 공부하는 컴퓨터 구조+운영체제
강민철 저자님과 함께하는 『혼자 공부하는 컴퓨터 구조+운영체제』 강의입니다. 다른 입문서에서는 알려주지 않았던 진짜 컴퓨터 공학 지식을 만나보세요! 👨🏫 누구를 위한 강의인가요? -
www.youtube.com
1. Intro
컴퓨터는 0과 1(컴퓨터가 주고받는 전기신호의 세기) 밖에 이해하지 못한다.
그런데 어떻게 0과 1이 아닌 다른 숫자를 알 수 있을까?
이번 장에서는 컴퓨터가 0과 1로 숫자를 표현하는 방법에 대해 알아보겠다.
2. 정보단위
비트(bit)
비트(bit)는 0과 1을 표현하는 가장 작은 정보 단위이다.

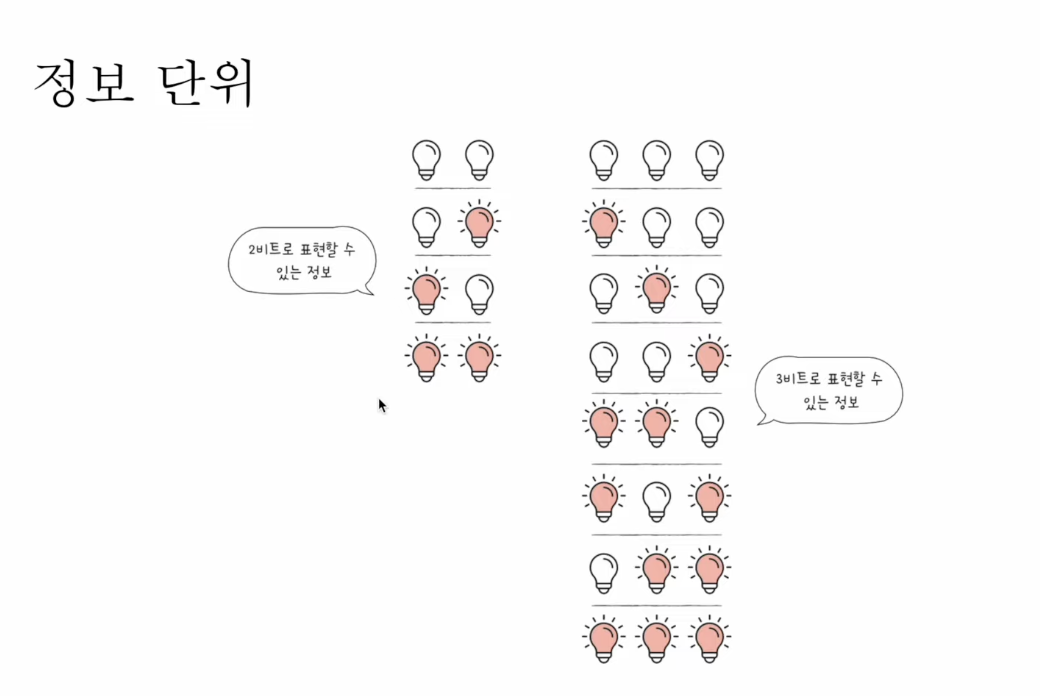
위와 총 $n$개의 bit로는 $2^{n}$가지의 정보로 표현가능하다.
프로그램은 수많은 비트로 이루어져 있는데,
평소 "이 파일은 8,920,120 bit야" 라고 표현하지는 않는다.
bit보다 더 큰 단위를 사용하는데, 그 종류로는 Byte(8bit), kiB($2^{10}$byte), MiB($2^{20}$byte), GiB($2^{30}$byte), 등이 있다.

워드 (word)
CPU가 한 번에 처리할 수 있는 정보의 크기 단위
하프 워드 (half word): 워드의 절반 크기
풀 워드 (full word): 워드 크기
더블 워드 (double word): 워드의 두 배 크기

3. 이진법: 0과 1로 숫자 표현하기
3.1) 이진법 (binary)
0과 1로 숫자를 표현하는 방법
숫자가 1을 넘어가는 시점에 자리올림
우리가 일반적으로 사용하는 10진법은 숫자가 9를 넘어갈 때 자리올림하는 십진법 (decimal)이다.
아래는 이진법으로 숫자를 표현하는 방식에 대한 사진이다.
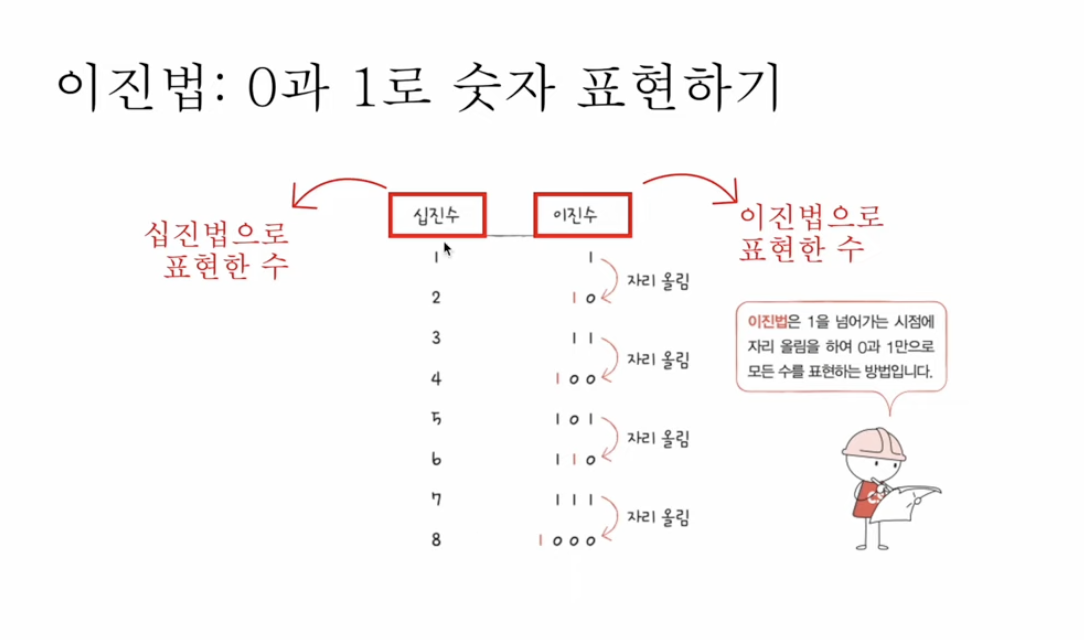
이진수로 표기하기 위해서는 2가지 방법이 있다.
- $(1000)_{(2)}$: 수학적 표기 방식, 숫자 아래에 괄호 $(2)$를 사용
- $ob1000$: 코드상 표기 방식, 앞에 $ob$ 붙이기
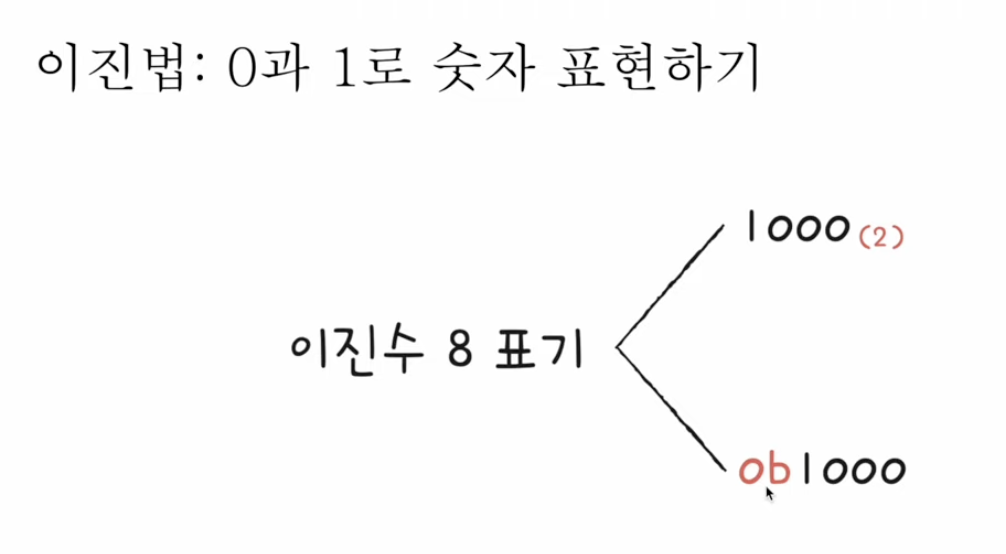
3.2) 이진법으로 음수 표현하기
컴퓨터는 (-) 부호를 인식하지 않기 때문에 0, 1만으로 음수를 표현해야 한다.
이때 사용하는 방법이 2의 보수법이다.
2의 보수법이란: 어떤 수를 그보다 큰 $2^{n}$에서 뺀 값을 2의 보수라고 하는데
$-N = C(N)$으로 처리한다.
이때 $C( )$: 2's Complement Operation 이다.
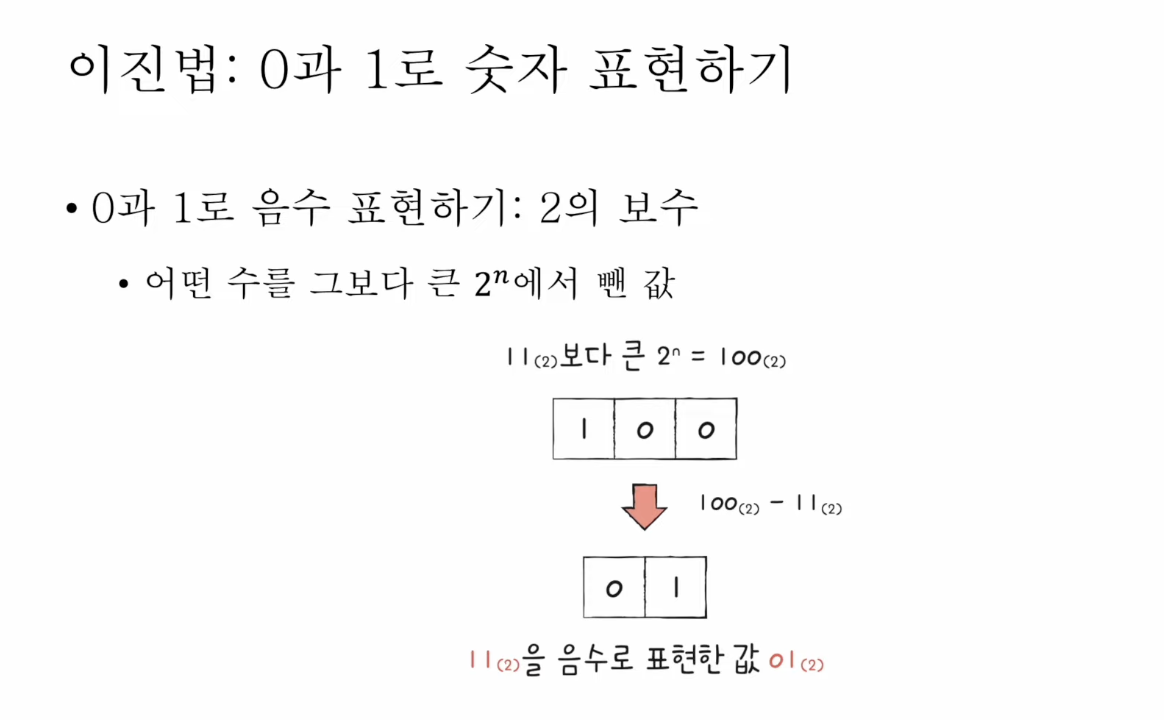

다만, 2's Complement의 경우 0과 1을 뒤집고 1을 더해주면 쉽게 구할 수 있다.
음수를 두 번 취해서 위의 방법이 맞는지 확인해보자.
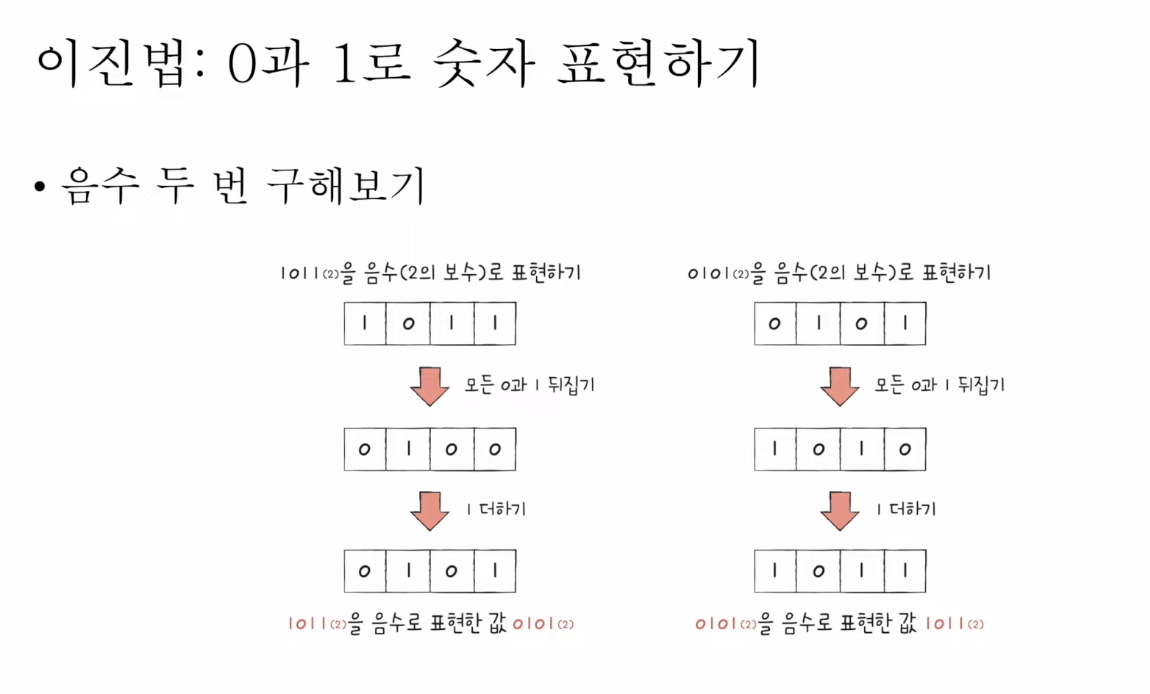
그렇다면, $-1011_{(2)}$를 표현하기 위한 2's Complement인 $0101_{(2)}$ 과 실제 십진수 5를 표현하기 위한
이진수 $0101_{(2)}$는 똑같이 생겼는데 이를 어떻게 구별하는지 궁금해할 수 있다.

둘을 구분하는 방법은 Flag Register에 저장된 값으로 구별한다.
CPU 내부에서 Flag Register에 현재 값이 음수인지 양수인지 표시를 해준다.
즉, 모든 숫자가 양수인지 음수인지 구별하는 Flag 를 들고 다니고 있기에 헷갈릴 일은 없다고 보면 된다.

4. 십육진법
이진법으로 숫자를 표현하다 보면, 숫자의 길이가 꽤나 길어지는 현상을 확인할 수 있다.
이럴 경우, 컴퓨터의 데이터를 표현할 때 수가 15를 넘어가는 시점에 자리올림을 하는 십육진법을 사용한다.

16진법에서는 하나의 digit당 숫자로는 0 ~ 9까지만 표현이 가능하므로 10의 'A' 부터 15의 'F' 와 같은 알파벳을 사용한다.

각 알파벳에 대응하는 숫자를 외우는 Tip은 다음과 같다.
A부터 주먹을 쥐고, B부터 알파벳이 뒤로 갈수록 손가락을 하나씩 핀다.
그렇게 최종 알파벳에 다다랐을 때, 펴진 손가락의 개수가 십진법으로 봤을 때 일의 자리의 수가 되는 것이다.

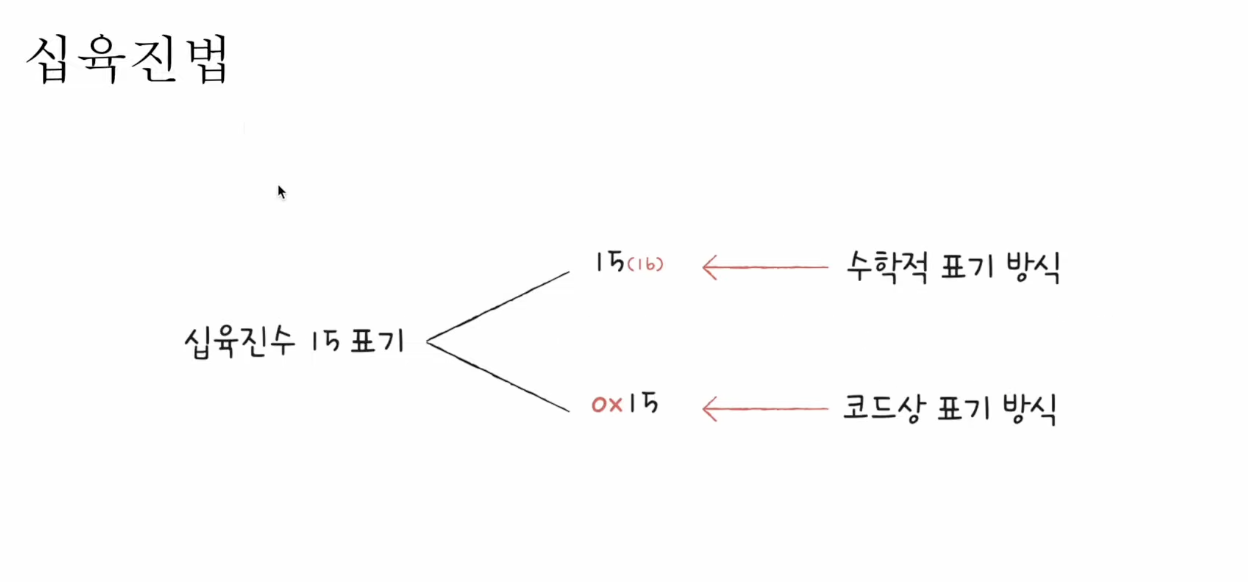
십육진수로 표기하기 위해서는 2가지 방법이 있다.
- $(15)_{(16)}$: 수학적 표기 방식, 숫자 아래에 괄호 $(16)$를 사용
- $ox15$: 코드상 표기 방식, 앞에 $ox$ 붙이기
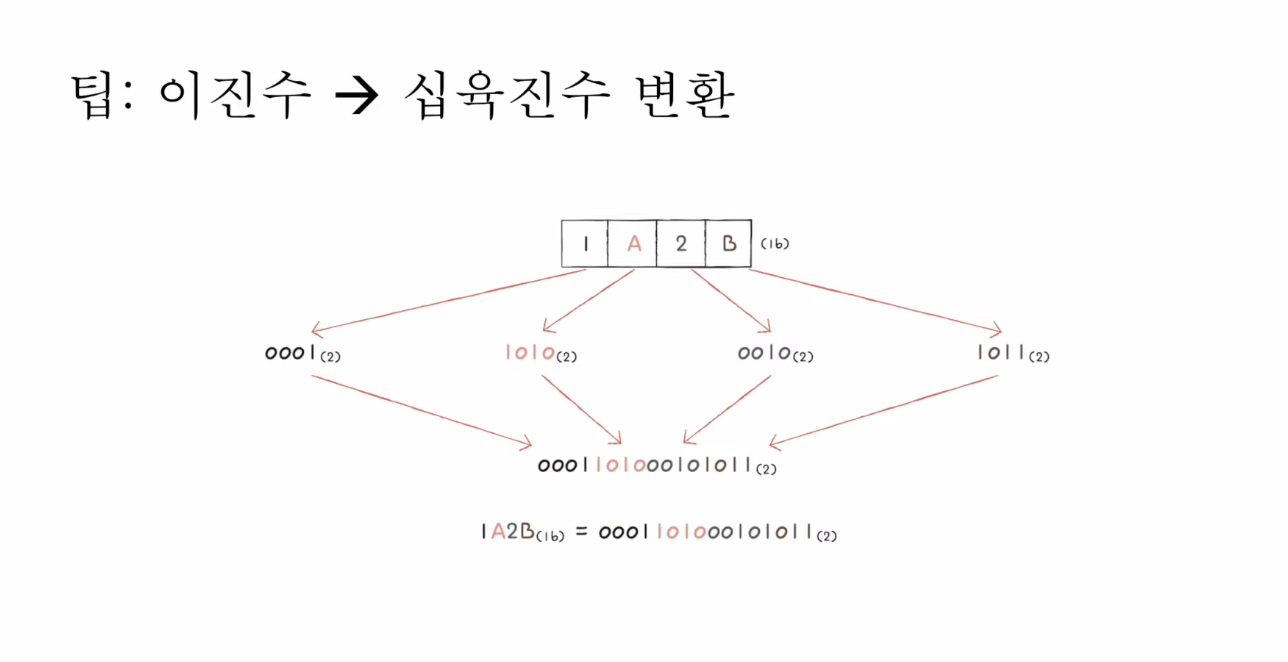
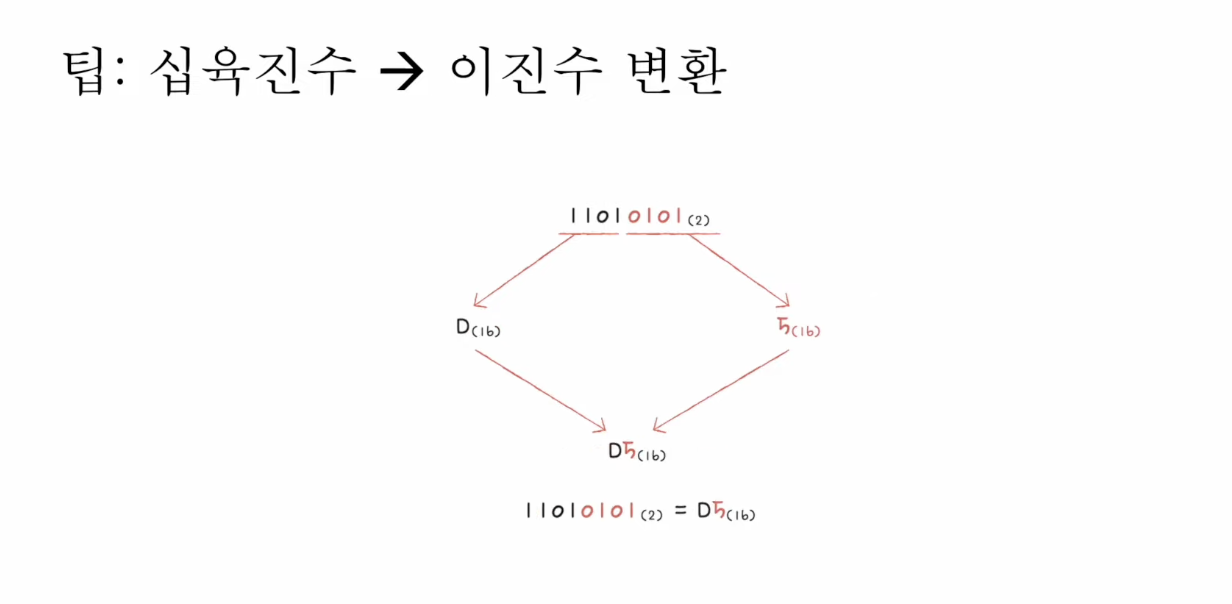
이진법과 비슷하게 십육진법을 사용하는 이유는 두 진법간의 전환이 십진법을 사용하는 것보다 편리하기 때문이다.
십육진수 -> 이진수: Digit 하나를 4비트로 표현해서 Concatenate
0
이진수 -> 십육진수: 4 Digit씩 묶어서 한 덩어리를 십육진수로 처리