0. Abstract
해당 논문에서는 두 가지의 Model(Discriminator, Generator)을 Adversarial Process를 통해 동시에 훈련하는 Generative Model의 아이디어를 제안한다.
Discriminator(판별자)는 Generator가 만든 Fake Data가 아닌 Real Data의 확률분포를 추정하고, Generator(생성자)는 임의의 Noise를 Sampling하여 Real Data와 유사한 분포를 Mapping(생성)한다.
이때, Generator는 Discriminator가 자신이 만든 Fake Data를 Real Data로 착각하도록 하는 확률을 최대화하도록 한다.
이러한 학습 구조를
minimax two-player game
이라 한다.
나중에 보면 알겠지만,
$\min_{G} \max_{D} V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{z}(z)}[\log (1 - D(G(z)))]$ 으로 Value Function을 정의하기에
Generator는 Value를 Minimize 시켜야 하고, Discriminator는 Value를 Maximize 시켜야 한다.

임의의 Discriminator와 Generator에 대하여 unique solution이 존재한다면
Generator는 Real Data(Training Data)의 Probability Distribution을 완벽하게 복원하는 것이고
Discriminator는 임의의 Input Data에 대한 정답확률을 항상 $\frac {1} {2}$로 반환하는 것이다.
Discriminator가 $\frac {1} {2}$의 정답 확률을 갖는 이유는
Generator가 real data의 확률분포를 완벽하게 복원하게 된다면
Discriminator는 들어온 input에 대하여 real인지 fake인지 구별할 수 없게 된다.
즉, Random하게 맞거나 틀리게 되므로 항상 $0.5$의 확률을 갖는다.
논문에서는 G와 D 모두 MLP(Multi-Layer Perceptron)으로 구성되어 있기에 backpropagation을 통해 훈련이 가능하다고 말한다.
즉, Markov chains 이나 Unrolled approximate inference networks가 이제 필요하지 않다고 주장한다.
이렇게 주장을 하는 이유는 GAN 이전의 Generative Model의 발전 흐름이
Markov chains 이나 Unrolled approximate inference networks를 사용했기 때문이다.
위의 내용들을 반영한 이전의 Generative Model들은 VAE(Variational AutoEncoders), Restricted Boltzmann Machines 들이 있다.
In Ian Goodfellow et al's paper "Generative Adversarial Networks", why do they specify that they do not need a Markov chain or i
In Ian Goodfellow et al's paper Generative Adversarial Networks, they state, "There is no need for any Markov chains or unrolled approximate inference networks during either training or generation of
stats.stackexchange.com

1. Introduction
GAN 이전의 Deep Learning이 작동하는 방식은 각 Input data의 종류(natural images, audio waveforms, etc.)에 맞춰 모집단에 근사하는 Probability Distribution을 나타내는 rich, hierarchical(다양한, 계층적) Model을 찾는 것이었다
따라서, Discriminative Model의 경우 고차원의 정제된 데이터를 Class Label에 1:1 Mapping 하여 구분하는 모델을 사용했다.
well-behaved gradient를 부분적으로 갖는 선형 활성화 함수(ReLU)들을 사용했고,
이들을 기반으로 한 Backpropagation, Dropout 알고리즘들에 기반했다.
이에 비해 Deep Generative Model들은 크게 2가지의 어려움이 있었다.
- Maximum likelihood estimation과 관련된 전략들에서 발생하는 많은 확률 연산들을 근사하는데 발생하는 어려움
- Generative Context에서는 앞선 Discriminative Model의 성공을 이끌었던 선형 활성화 함수들의 이점을 사용하는데 어려움
difficulty of approximating many intractable probabilistic computations 에서
"intractable computation"은 컴퓨터로 할 수 없는 계산을 의미한다.
즉, 컴퓨터로 계산할 수 없는 확률을 보통 계산할 수 있도록 근사를 해서 푸는데, 이것 마저 어렵다는 뜻이다.
여기서 intractable의 기준은 다항시간 내에 풀 수 없는 문제를 의미하는데(intratable, NP Problem), 3차 이상의 시간복잡도를 갖는 알고리즘을 $O(n^{k})$이라 한다.
결과적으로 기존의 Generative Model들은 컴퓨터로 계산할 수 없는 intractable computation 과정을 근사하여 푸는 것 조차 어려웠기 때문에 성장하지 못했다는 뜻이다.
결국 논문에서는 이러한 한계점들을 극복하지 않고, 회피하여 새로운 Generative Model을 제안한다.
제안된 구조는 Adversarial nets framework로, Generative Model이 Discriminative Model과 서로 경쟁하는 구조이다.
Discriminative Model은 주어진 sample data가 Generative Model이 생성한 Fake Data인지, 아니면 Training Data인 Real Data인지 구별하는 것을 학습한다.
sample from the model distribution: Fake Data
sample from the data distribution: Real Data
위의 내용을 더 간단히 설명하기 위해 너무나 유명한 예시를 가져왔다.
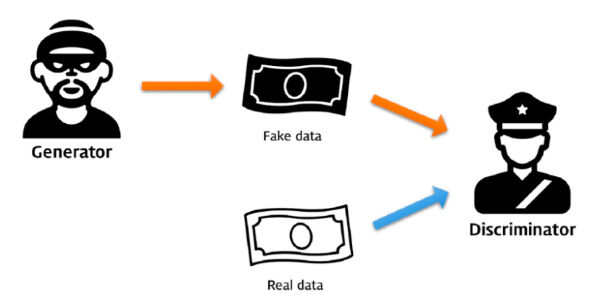
GAN의 경쟁 과정을 경찰(Discriminator)과 위조지폐범(Generator) 사이의 경쟁으로 바라보자.
위조지폐범은 최대한 실제 화폐와 비슷한 화폐를 만들어, 경찰을 속이기 위해 노력한다. 경찰은 진짜 화폐와 위조지폐범이 만든 가짜 화폐를 완벽하게 구분하여 위조지폐범을 검거하는 것을 목표로 삼는다.
따라서, 위의 과정을 반복하다 보면 다음과 같은 순간에 도달한다.
위조지폐범이 진짜와 다를 바 없는 위조지폐를 만들게 되고, 그 결과 경찰은 실제 지폐와 위조 지폐간의 차이를 구분할 수 없고 위조지폐를 구별할 수 있는 확률이 50%에 수렴하게 된다.
즉, GAN의 목적은 각각의 역할을 가진 Discriminator와 Generator를 이용하여 Real Data의 확률분포를 따르는 Fake Data를 생성해내는 능력을 키워주는 것이라 할 수 있다.
이러한 Framework는 많은 training algorithm과 다양한 종류의 model, optimization algorithm들을 사용할 수 있다.
특히나 special한 case인 Generator와 Discriminator 모두 MLP(Multi-Layer Perceptron)를 사용할 경우 저자들은 이를 'adversarial nets'라 한다.
Adversarial Nets의 경우
1. Discriminator와 Generator 모두를 highly successful한 backpropagtion과 dropout algorithm 으로 학습이 가능하다.
2. Generator가 only foward propagation을 통해 noise로부터 sampling이 가능하다.
2. Related Work
Related Work 부분에서는 이전까지 수행됐던 Generative Model에 관한 Review가 진행된다.
Boltzmann Machine, Restricted Boltzmann Machine, Variational AutoEncoders(VAE) 등은 추후에 해당 분야에 대해 학습을 마친 후 작성하도록 하겠다.
VAE에서 사용한 variational inference (approximate inference) 기법이나,
Traditional Generative Model에서 사용된 Markov Chains 등을 사용하지 않아도 된다는 점이 GAN의 큰 장점이다.
3. Adversarial nets
Discriminator, Generator 모두가 MLP(Multi-layer perceptron) 구조일 때, Adversarial Modeling Framework를 적용하기가 가장 용이하다.
3.1) Value Function
Data $x$에 대해 Generator의 분포 $P_{g}$를 배우기 위해 먼저 noise 변수 $P_{z}(z)$를 정의한다.
그리고 noise $z$를 sampling하여 $G(z; \theta_{g})$를 통해 Data Space에 Mapping 시키는데, 이때 $G$는 미분가능한 함수로 parameter $\theta_{g}$를 갖는 MLP로 나타난다.
$G(z; \theta_{g})$는 $z$라는 noise를 sampling하여 Data Space에 분포를 Mapping 해주는 역할을 한다.
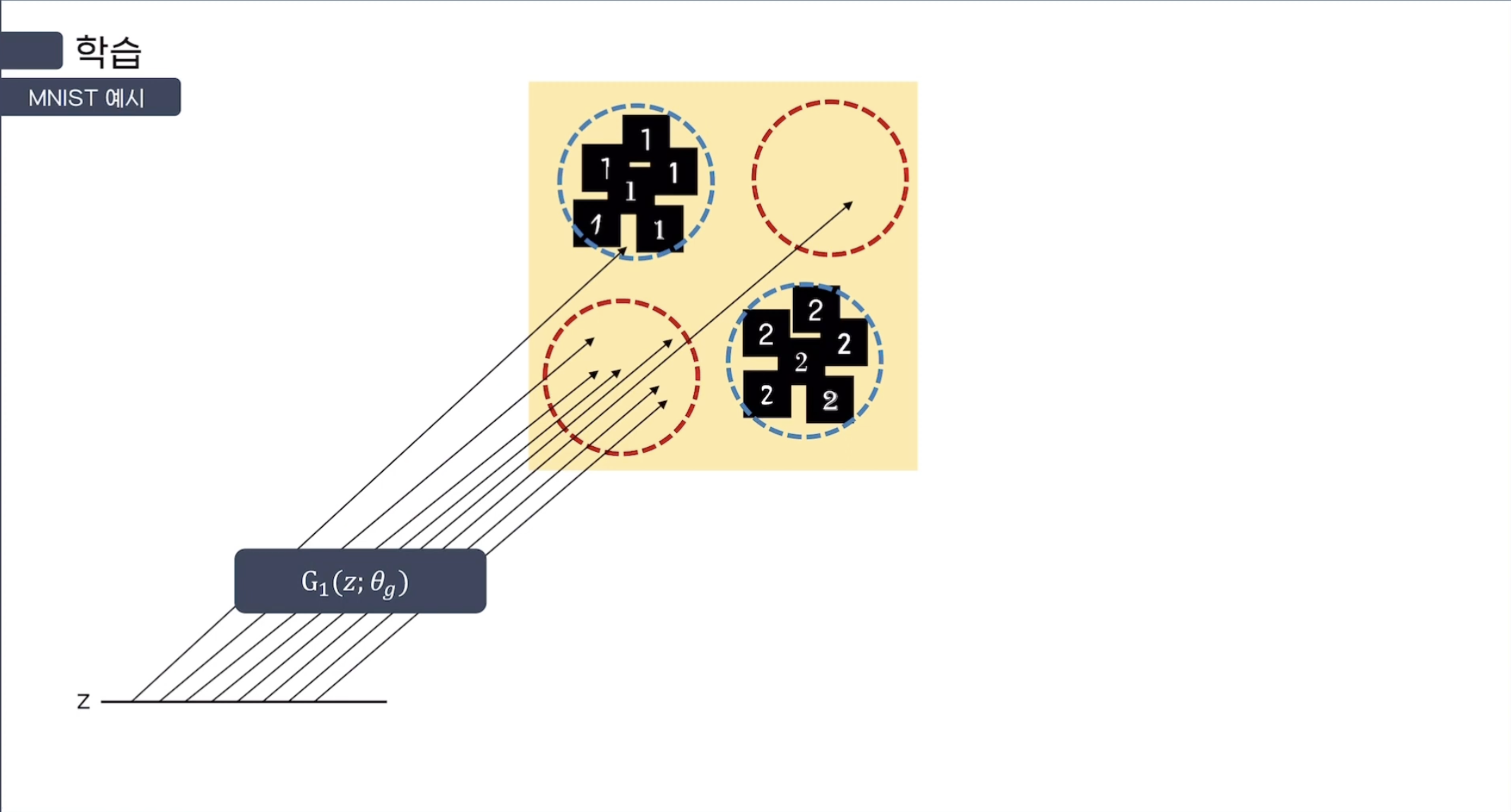
예시를 들기 위해, 1과 2만 있는 MNIST Dataset을 생각해보자.
다음과 같이 784(28*28)개의 pixel을 Data Space에 나타난다고 했을 때,
위의 그림처럼 나오면 2, 아래의 그림처럼 나오면 1로 성공적으로 Mapping이 되었다고 볼 수 있다.
처음에는 Mapping시 원하는 Domain 안으로 Mapping 되지 않지만,
학습이 진행될수록 Generator의 Mapping이 원하는 Domain 안으로 떨어지는 것을 볼 수 있다.
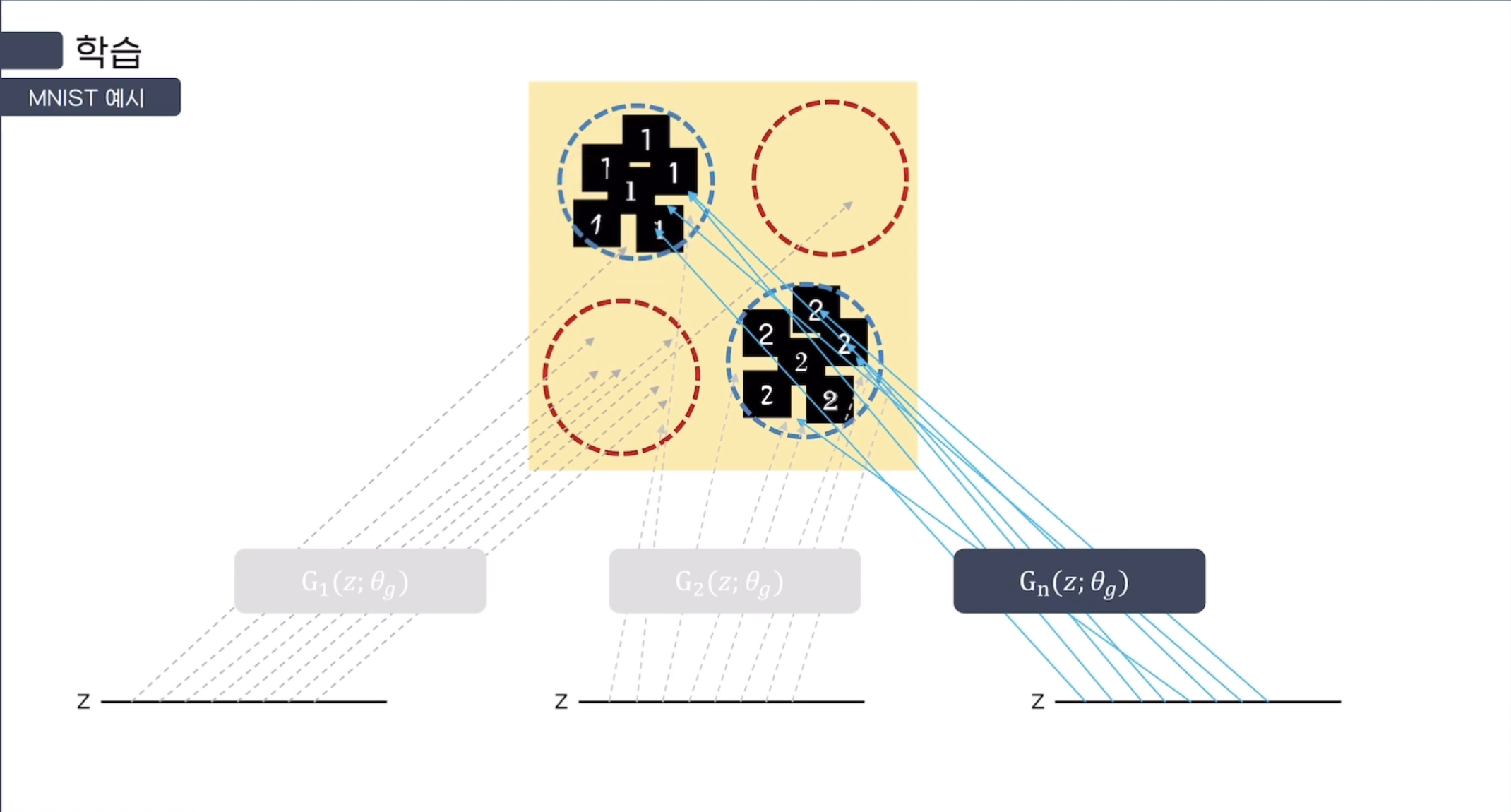
MLP로 이루어진 $D(x; \theta_{d})$도 정의하는데, output은 scalar(0 ~ 1)이다. $D(x)$는 $x$가 real image에서 나온 확률을 의미한다.
$D$를 real image와 $G$에서 나온 sample에 올바른 label을 붙일 수 있도록 학습시키고 $log (1- D(G(z)))$를 minimize 시키게 $G$를 학습시킨다.
$\min_{G} \max_{D} V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{z}(z)}[\log (1 - D(G(z)))]$
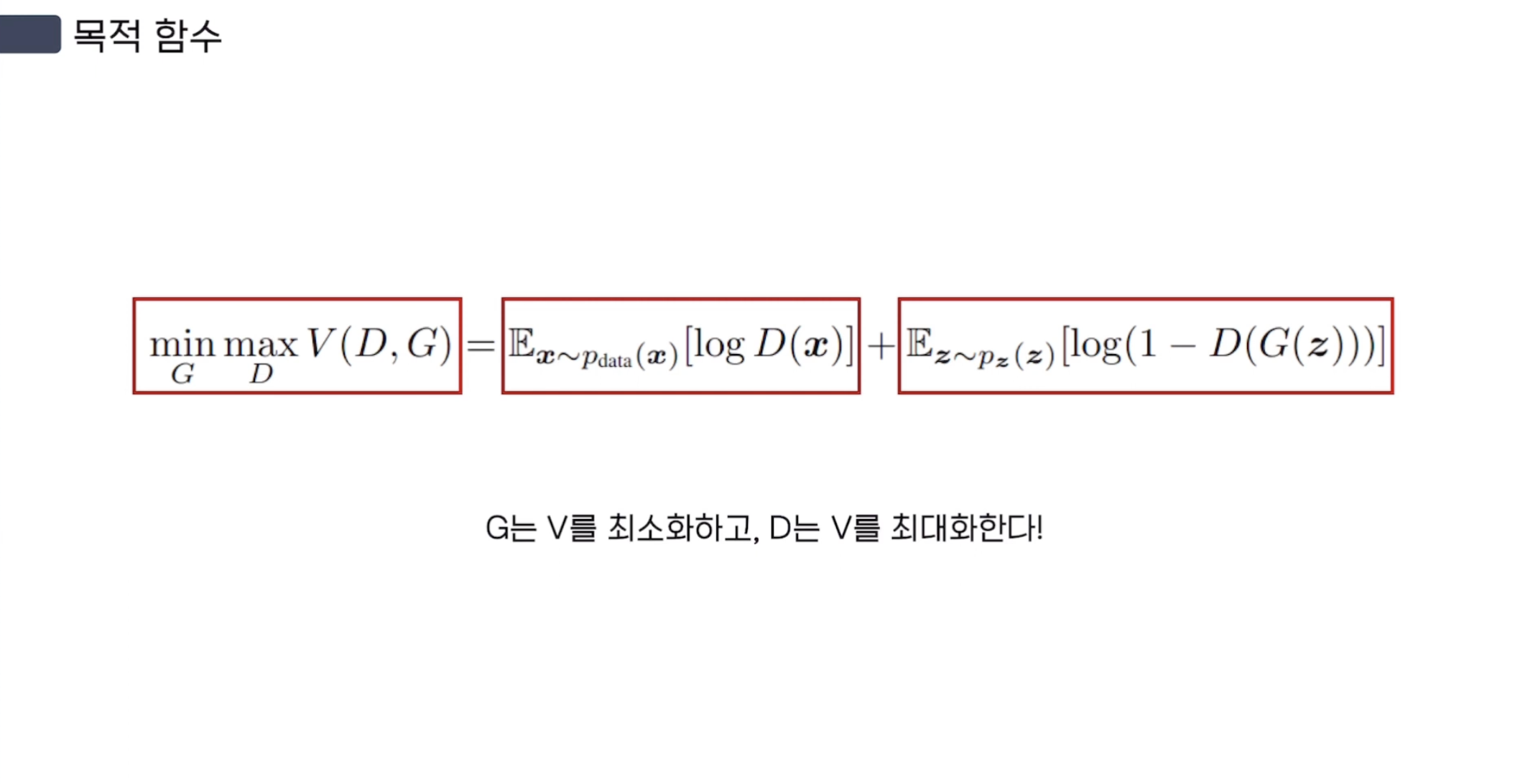
1. noise 분포 $P_z$에 noise $z$를 입력으로 넣어 $P_{z}(z)$로, noise를 sampling한다.
2. noise를 G에 input으로 넣는다. G는 $\theta_{g}$를 parameter로 갖는 MLP이다.
3. $D$는 real image와 $G$가 생성해낸 fake image를 구별할 확률을 Maximize 한다.
4. G는 $log(1-D(G(z)))$를 Minimize 한다.
$D(G(z))$는 $D$가 $G$에서 나온 fake image를 구별하는 과정이다.
따라서 $G$의 입장에서는 자신이 만든 fake image가 $D$는 구별할 수 없도록,
real image label인 1을 scalar로 반환하도록 만들어야 한다.
즉, $log(1-1) = log(0) = -\infty$ 로 Minimize 되도록 $G$가 노력하는 것이다.
일단 용어부터 먼저 정리하자.
- $P_{data}$: real image의 probability distribution(확률 분포)
- $P_{z}$: noisze의 probability distribution(확률 분포)
- $\mathbb{E}_{x\sim p_{\text{data}}(x)}$: $x$가 real data의 확률분포를 따른다 = $x$를 real data로부터 가지고 왔다
$\mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)]$: $D$가 $x$를 $P_{data}$, 즉 real data로부터 가지고 있다고 판단할 확률의 기댓값이다
- $\mathbb{E}_{z\sim p_{z}(z)}$: $z$가 특정 noise 분포를 따른다 = 해당 분포를 따르는 noise $z$를 sampling 했다
$\mathbb{E}_{z\sim p_{z}(z)}[\log (1 - D(G(z)))]$: $D$가 $G(z)$, 즉 noise를 통해 생성한 fake data를 fake data로 판단할 확률의 기댓값이다
Discriminator의 관점
따라서 Discriminator는 기댓값을 Maximize, $\mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)]$에서는 $D(x)$를 1(real image)로 판단하고, $\mathbb{E}_{z\sim p_{z}(z)}[\log (1 - D(G(z)))]$에서는 $D(G(z))$를 0(fake image)으로 판단하도록 한다.

Generator의 관점
Generator는 기댓값을 Minimize, 즉 $\mathbb{E}_{z\sim p_{z}(z)}[\log (1 - D(G(z)))]$에서는 $D(G(z))$를 $D$가 1(real image)로 판단하도록 한다.

3.2) GAN Training Process
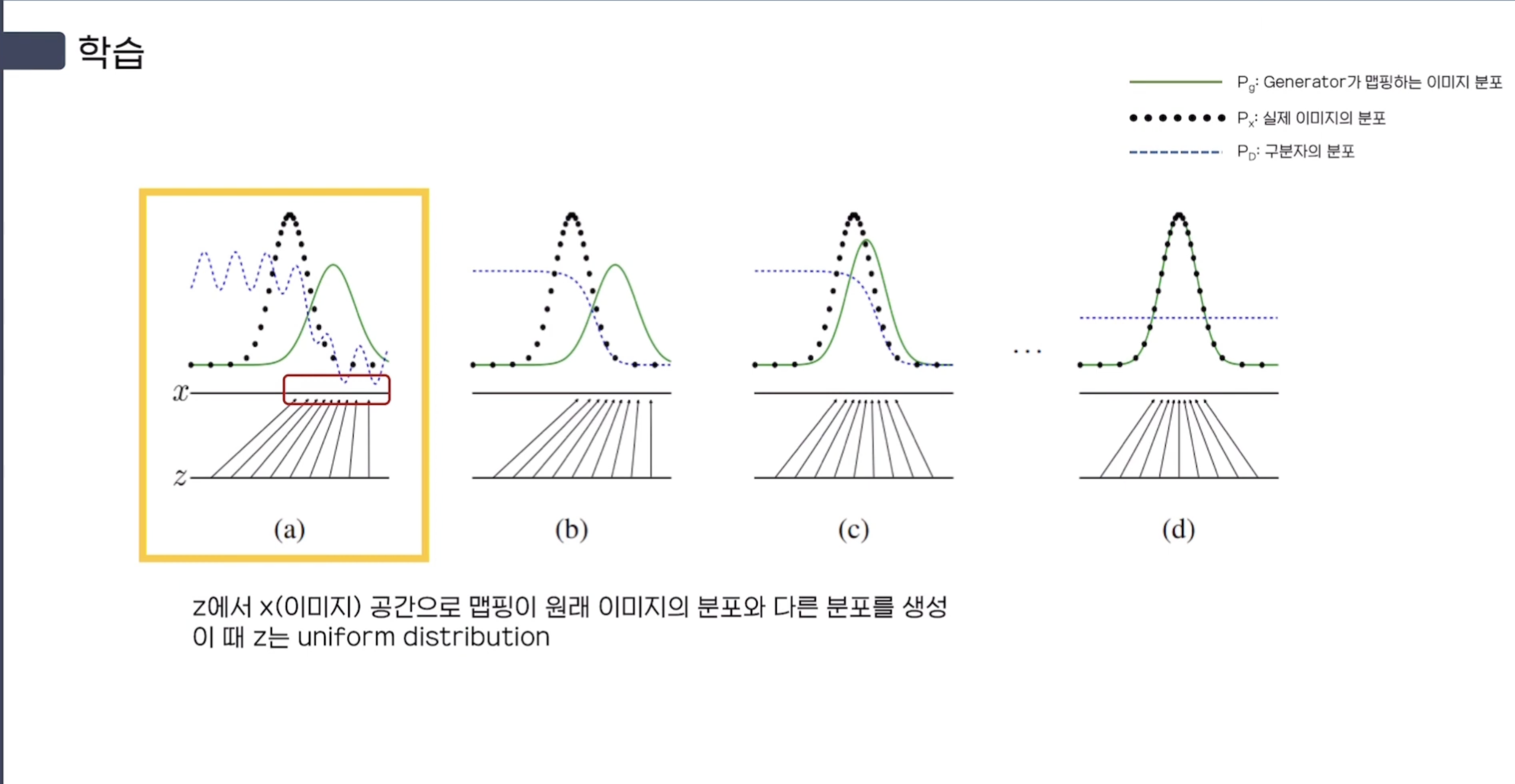
(a) 초반에는 noise $z$에서 Generator를 통해 image space $x$로 mapping 시켜준다.
다만 초기 step에서는 해당 Mapping(Green)이 원래 이미지의 분포(Black)와 다르다.
uniform distribution을 따르는 $z$는 $x = G(z)$으로의 Mapping을 통해 non-uniform distribution이 적용된다.
Q1. Input Noise $z$를 uniform sampling말고 gaussian sampling을 하는 건 안되는가?
A. 가능하다. GAN 방식 자체가 $z$의 확률분포가 무엇인지와 별개로 image data의 확률분포를 estimation 할 수 있다.
Generative Model의 목적은 image data의 확률 분포를 maximum likelihood 하기를 원한다.
하지만 image data의 확률 분포를 한 번에 아는 것은 쉽지 않기 때문에 Training을 통해 Generative Model을 image data의 확률 분포에 maximum likelihood 하도록 estimation (추정) 하는 것이다. 이렇게 추정을 하는 방식은 아래와 같이 두 가지로 나뉜다.
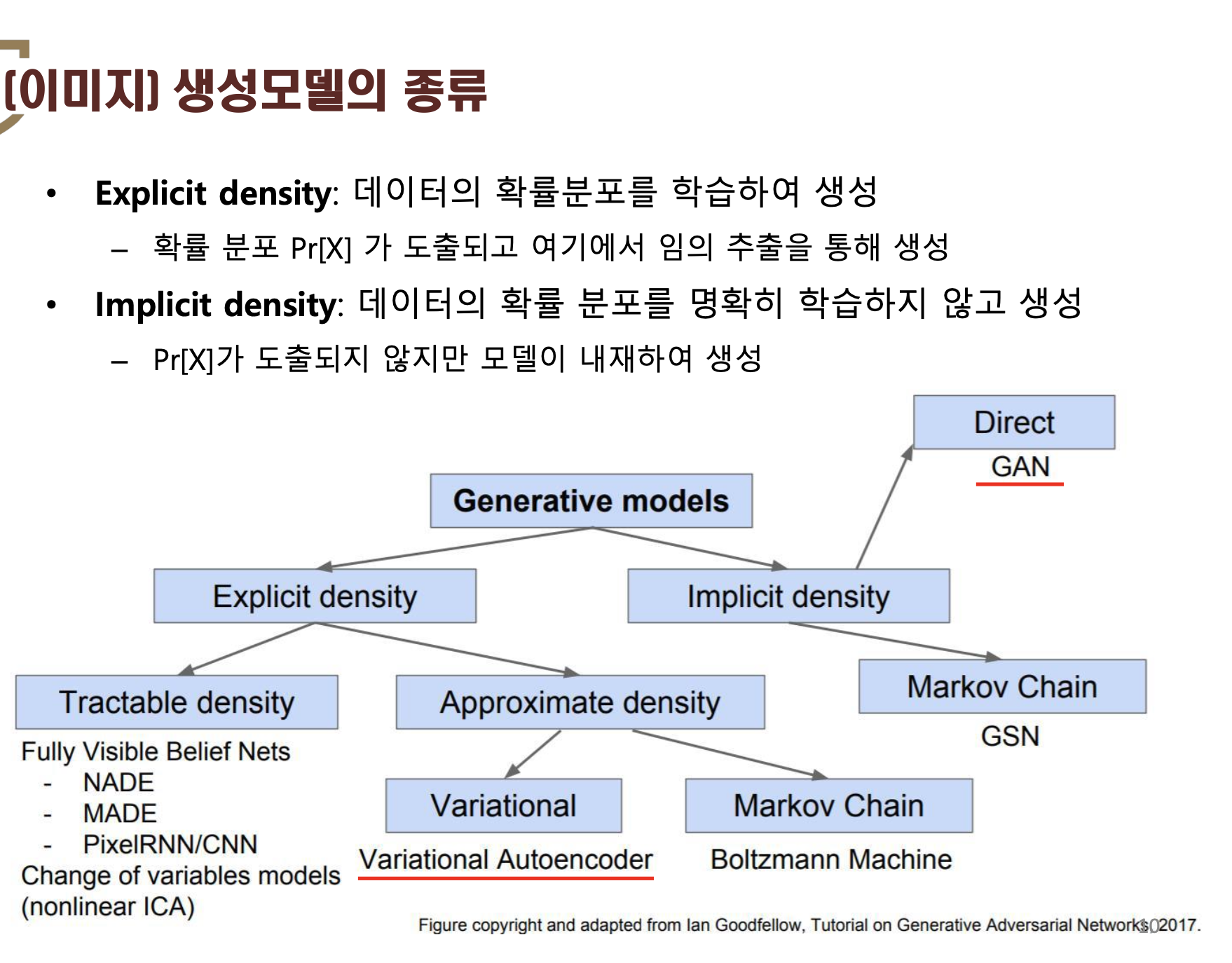
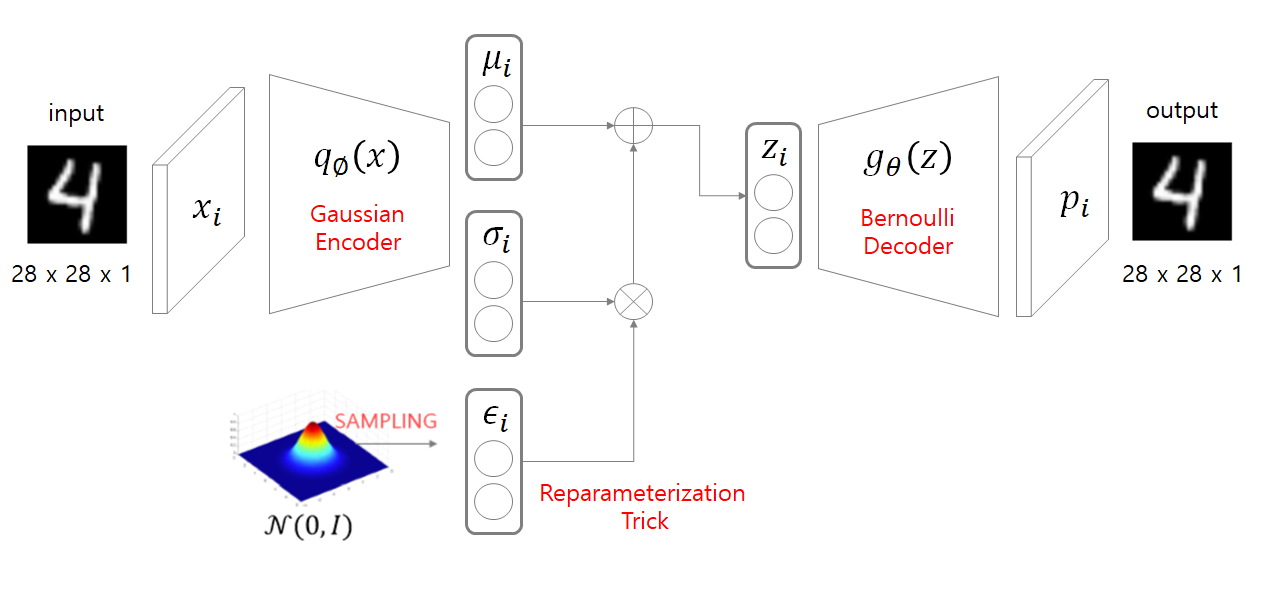
첫 번째 방식은 Explicit density이다. 예를 들어, VAE에서는 image data의 확률 분포 $x \sim p_{x}(x)$ or $x \sim p_{data}(x)$를 표현해주기 위해 이상적인 noise $z$값을 sampling 하기를 원한다.
즉, 이상적인 noise $z$의 확률분포인 $z \sim p_{z}(z)$ or $p_{z \sim latent}(z)$을 알아내고 싶은 것이다.
그렇기 때문에 VAE 모델은 사전에 명시적(explicit)으로 $z$의 확률분포인 $p_{z \sim latent}(z)$가 특정 probability distribution인 gaussian distribution을 따를 것이라 가정한다.
특히 VAE에서 초기에 설정한 density estimation 수식은 intractable 했기 때문에 이를 variational inference를 이용해 approximation하도록 하여 tractable 하게 바꾸게 된다.
두 번째 방식은 GAN과 같은 implicit density 방식이다.
앞서 언급한 VAE처럼 Explicit density(명시된 사전 확률분포)를 이용하는 것이 아니라 사전에 어떠한 확률 분포도 명시하지 않는다.
즉, noise $z$의 확률 분포가 특정 확률 분포를 따라야 한다는 가정이 없어도 된다는 뜻이다.
따라서 앞서 input noise인 $z$를 sampling할 때, $z$가 uniform distribution을 따른다는 가정하에 sampling을 해도 되고
gaussian distribution을 따른다는 가정하에 sampling을 해도 되는 것이다.
정리하면 GAN 방식을 이용한 Generative Model은 input noise $z$의 확률 분포가 무엇인지와는 별개로 image data의 확률 분포를 estimation(추정)할 수 있게 된다.
Since an adversarial learning method is adopted, we need not care about approximating intractable density functions.
앞의 VAE에서 intractable 하다고 했던 이유는 사전에 explicit하게 정의된 input noise $z$의 probability distribution(=density function)때문이라고 했는데,
GAN에서는 input noise $z$의 probability distribution에 대한 제약이 없기 때문에 애초에 intractable density function을 approximate할 필요가 없게 된다.
(b) Generator의 가중치를 Freeze(고정)하고, Discriminator를 학습한다.
Real Image에 대해 안정적으로 1에 가까운 확률, Fake Image에 대해 안정적으로 0에 가까운 확률을 반환하도록 학습한다.
그림을 보면 $P_{D}$인 Discriminator 분포가 (a)에 대해 안정적인 형태를 띄고 있음을 알 수 있다.
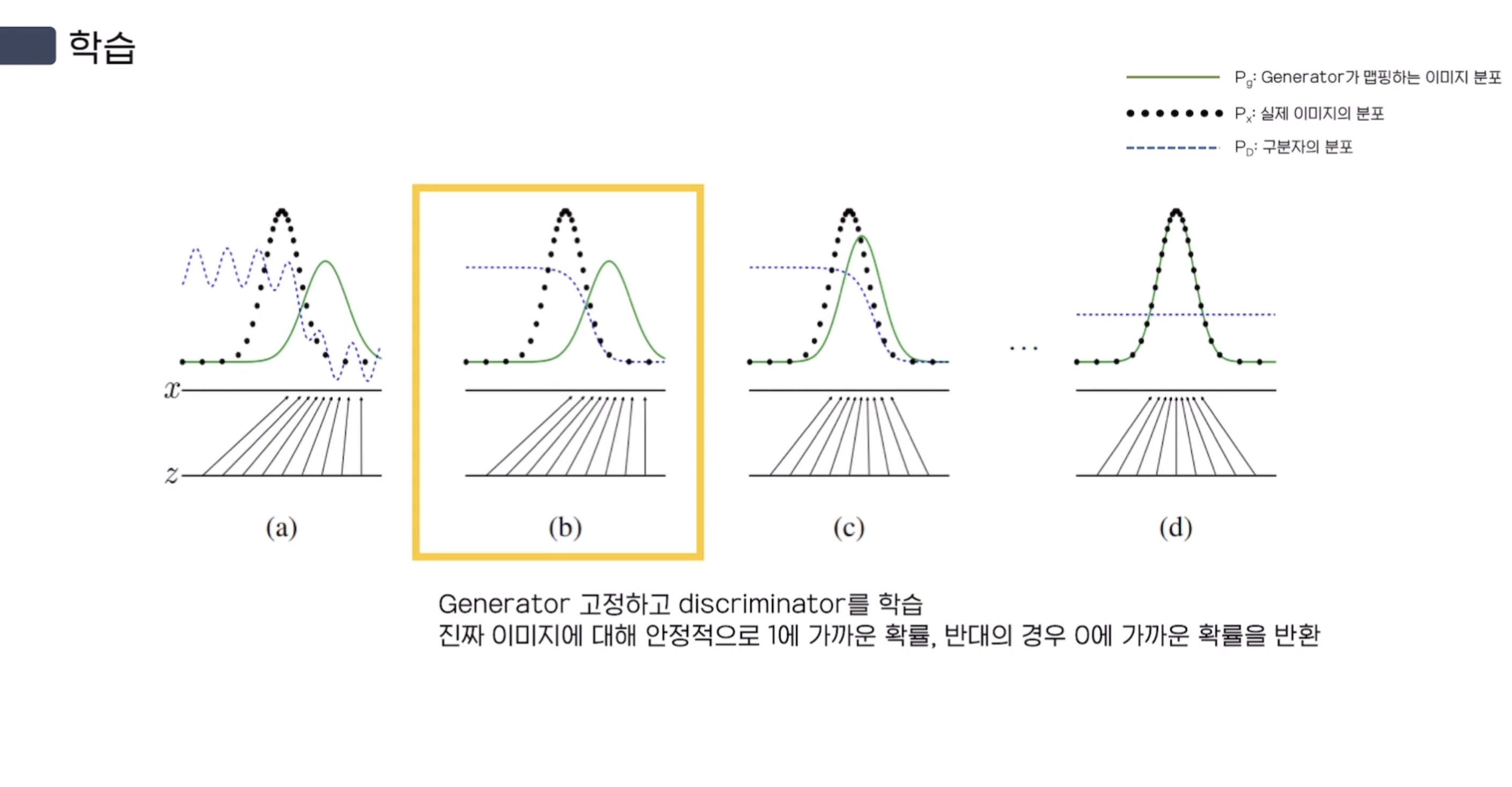
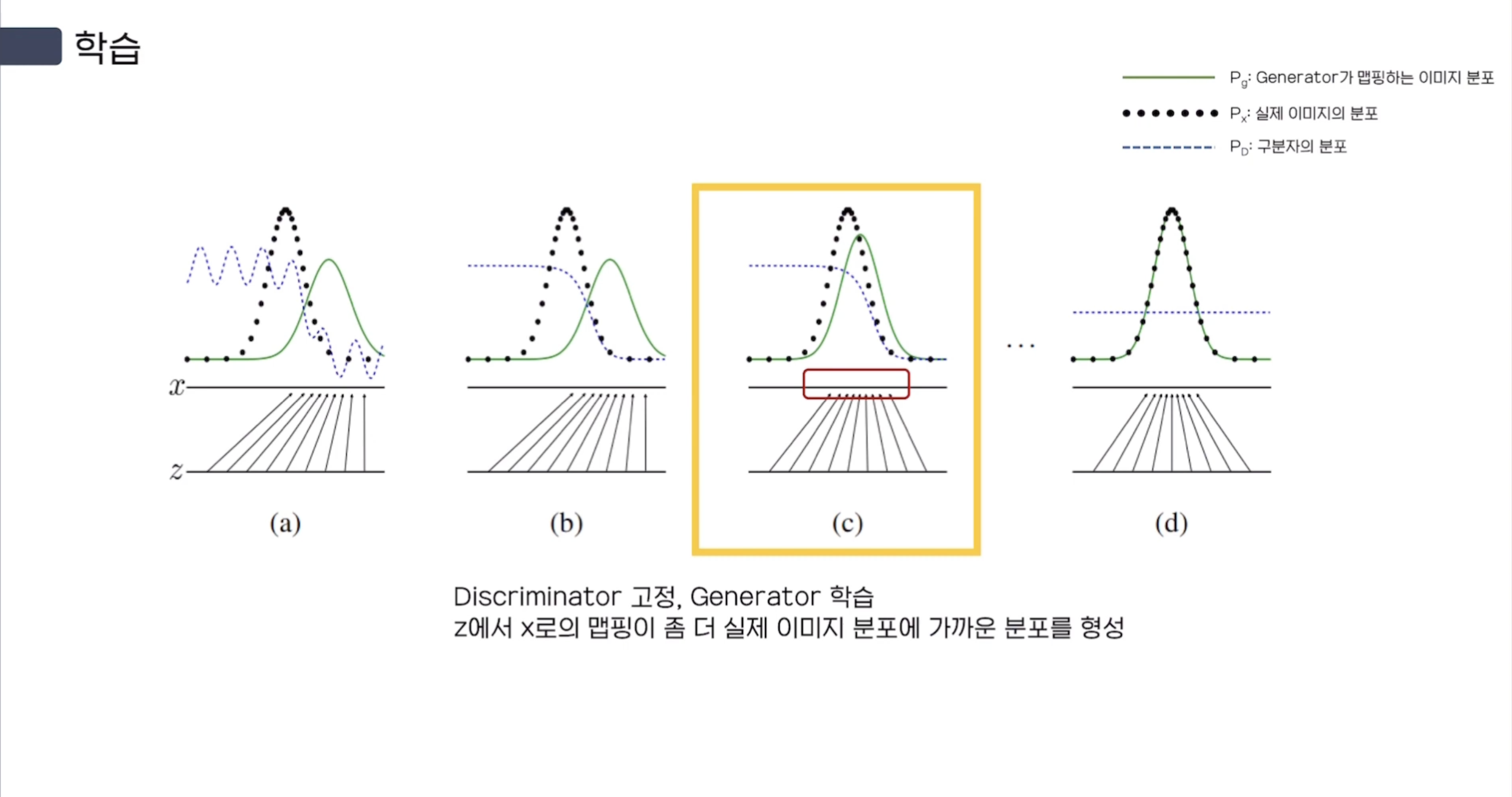
(c) Discriminator를 Freeze(고정)시키고, Generator를 학습한다.
$x = G(z)$의 Mapping이 조금 더 실제 이미지 분포에 가까운 분포를 형성한다.
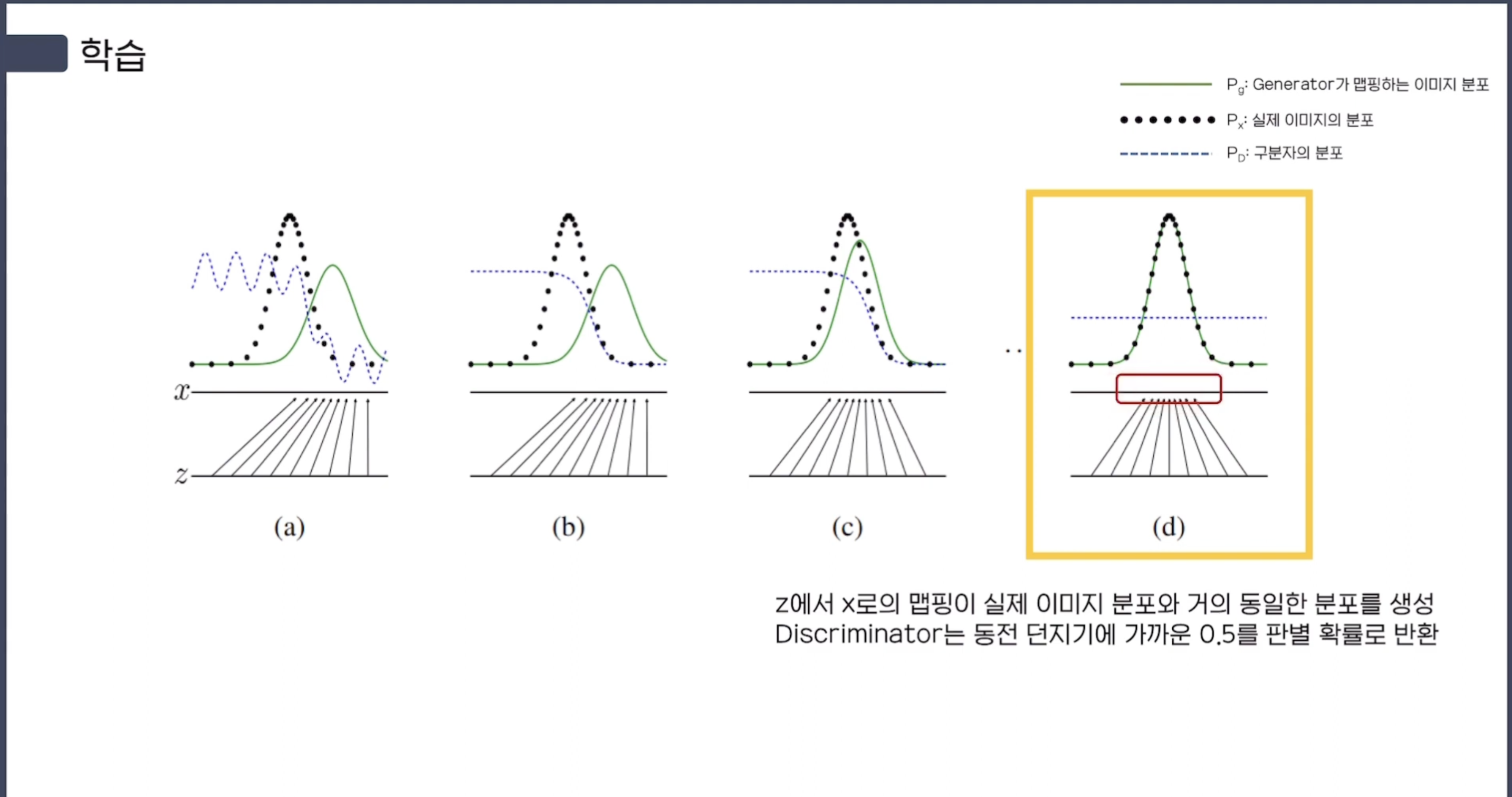
(d) Training을 여러 번 완료한 후에, G와 D가 둘다 enough capacity가 있다면
$x = G(z)$인 $z$에서 $x$로의 Mapping이 real data의 분포와 거의 동일한 분포를 형성한다. ($p_{g} = p_{data}$)
그에 따라 Discriminator 또한 real data와 Generator가 생성한 fake data 사이를 구별하지 못하기 때문에,
그냥 random에 의한 동전 던지기로 $\frac {1} {2}$를 판별 확률로 반환하게 된다. ($D(x) = \frac {1} {2}$)
실제 Blue, dashed line을 보면 딱 절반만큼의 확률인 $0.5$로 수렴한 것을 볼 수 있다.
또한 training loop 안에서 $D$만 최적화하는 것은 overfitting의 가능성이 존재하기 때문에,
$D$를 최적화하는 k step과, $G$를 최적화하는 one step을 서로 번갈아 훈련을 시켜야 한다.
3.3) Non - Saturating Game
저자들은 위의 Training Process에서 하나의 문제점을 지적한다.
그것은 바로 Generator가 학습 초반에 real data의 분포와는 전혀 다른 분포를 갖게 된다는 점이다.
그에 따라 Discriminator는 높은 confidence score를 가지고 매우 쉽게 real image와 Generator가 생성한 조잡한 fake image를 구별할 수 있게 되고, 이는 학습이 제대로 진행되지 않는 문제를 야기한다.
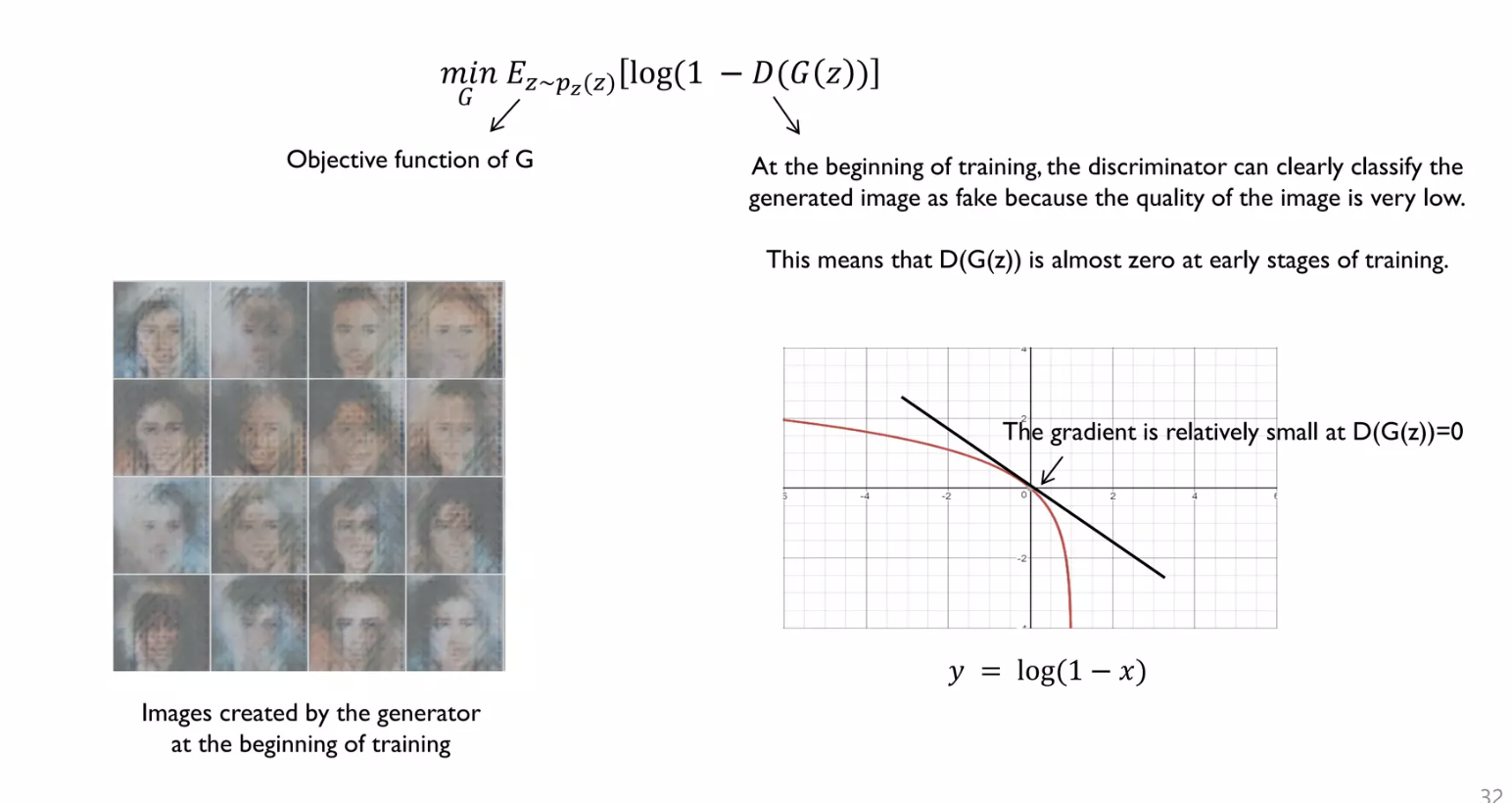
학습이 제대로 진행되지 않는 이유는, update되는 Gradient 값이 saturation된 상태이기 때문에 update가 매우 느리기 때문이다.
초반에는 Generator가 정교하지 않은 조잡한 fake image를 생성하므로 Discriminator가 $G(z)$로 생성된 이미지를 Fake라고 잘 판별하게 된다. ($D(G(z)) = 0$)
그런데, $log(1-(D(G(z)))$ 꼴의 함수에서 초기 $D(G(z))$의 값이 0이 나온다면 gradient 값 자체가 saturation된 상태이기 때문에 update가 더딜 수 있다.
그렇기에 Generator를 학습시키는 관점을 $log(1-D(G(z))$를 Minimize 하는 것이 아니라, $log(D(G(z))$를 Maximize하는 방향으로 변경한다.
이러한 문제점을 해결하기 위해 Generator의 학습방향을 $log(1-D(G(z))$를 Minimize 하는 것이 아니라, $log(D(G(z))$를 Maximize하는 방향으로 설정한다.

$log(D(G(z)))$를 사용하여 Gradient를 더 빠르게 update하여 Generator가 성능이 안 좋은 상황을 최대한 빨리 벗어나려고 한다.
어차피 Generator의 입장에서는 $D(G(z)) = 1$이 되도록 G를 학습시키기만 하면 되기 때문에
$log(1-D(G(z)))$를 Minimize 한다 = $log(D(G(z)))$를 Maximize 한다 = $D(G(z)) = 1$을 반환하도록 한다
위의 세 개는 전부 같은 말이므로, 실제 학습이 사용되는 Value Function의 Term을 바꿔도 문제없다.
즉, 실제 학습에 사용되는 Value Function $V(D, G)$는 아래와 같이 변경된다.
$\min_{G} \max_{D} V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{z}(z)}[\log (1 - D(G(z)))]$ 가 기존에 사용된 식이였다면,
$\max_{G} \max_{D} V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{z}(z)}[\log (D(G(z)))]$ 으로 실제 학습에 사용된다.
위의 practical usage를 보면 Binary - Cross Entropy Loss를 사용한다.
여기서 Generator를 훈련시킬 때 Discriminator가 fake image(0)에 대해 real image(1)로 착각하게끔 해야 하므로
$D(G(z))$라는 value에 대해 label = 1로 설정해야 한다.
그 결과 $-\left[ y \log(h(x)) + (1 - y) \log(1 - h(x)) \right]$에 $h(x) = D(G(z)), y = 1$를 대입하면 되므로
$\min_{G} \mathbb{E}_{z \sim p_{z}(z)}[-\log D(G(z))] $가 된다.
결국 BCELoss를 사용하면 Generator를 훈련시킬 때 알아서 Non-Saturate되도록 Loss Function이 설정된다.
4. Theoretical Results
Generator $G$는 noise $z$가 특정 분포 $p_{z}$를 따를 때 $z \sim p_{z}$, noise를 sampling하여 Generator가 Image space로 Mapping하여 나오는 Fake Image의 분포 $p_{g}$를 암묵적으로 정의한다.
즉 충분한 capacity와 training time이 있다면 Generator가 생성한 Fake image의 분포 $p_{g}$를 실제 training set의 real image의 분포 $p_{data}$로 수렴시킬 수 있다.
아래에 설명된 Algorithm1은 설계한 Deep Learning Model의 Global Optimum을 찾는 Algorithm이다.

Deep Learning Model을 설계할 때에는 아래의 4가지 기준을 만족했는지 살펴봐야 한다.
물론 더 많은 기준이 있을 수 있겠으나, GAN 논문에서는 아래 4가지 정도로 요약했다.
또한 뒤에서 나오지만, 실제 Neural Network가 사용되면 아래의 기준을 이상적으로 만족하는 것이 불가능하다. 따라서 아래의 기준들은 DL Model 설계시 지향해야 하는 이상적인 Guideline 정도로 생각하면 된다.
1. 설계한 Deep Learning(Probability) Model이 Tractable 한가? (계산 시스템 관점에서 충분히 다룰 수 있는 알고리즘인가?)
2. 설계한 Deep Learning(Probability) Model이 Global Optimum을 갖는가?
3. 설계한 Deep Learning(Probability) Model이 Global Optimum에 수렴하는가?
4. 설계한 Deep Learning(Probability) Model이 Global Optimum을 찾을 수 있는 Algorithm이 존재하는가?
4.1) Global Optimality of $p_{g} = p_{data}$
설계한 Deep Learning(Probability) Model이 Global Optimum을 갖는가?
GAN의 최종 Value Function은 어떠한 값을 가져야 Global Optimum이라 할 수 있는가?
즉, 최종적으로 도달하고자 하는 loss 값은 무엇인가?
$\min_{G} \max_{D} V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{z}(z)}[\log (1 - D(G(z)))]$
Generator 관점에서 MinMax problem (value function)은 $p_{g} = p_{data}$에서 global optimum 값을 찾아야 한다.
직관적으로 봤을 때, Generator가 생성하는 fake data의 distribution인 $p_{g}$가
real data의 distribution인 $p_{data}$와 유사한 distribution을 형성하는 지점인 곳에서
global optimum 값을 찾게 되면 학습을 중단한다.
논문에서는 임의의 Generator에 대한 Optimal Discriminator의 global optimum 값은 다음 수식에 의해 도출된다고 설명한다.
$D_{G}^*(x) = \frac{P_{\text{data}}(x)}{P_{\text{data}}(x) + P_g(x)}$
위 수식의 직관적인 설명은 다음과 같은데,
$p_{g} = p_{data}$일 경우 $D_{G}^*(x) = \frac {1} {2}$의 값을 갖는다. 이는 Discriminator가 fake image와 real image를 판별할 확률이 모두 0.5라는 의미이다.
즉, 진짜와 가짜를 구별할 능력이 없기에 그냥 랜덤하게 절반의 확률로 판별한다는 것이다.
그러므로 GAN의 Loss Function인 $V(D,G)$에서 $D_{G}^*(x) = \frac {1} {2}$에 수렴한다면 학습을 종료하면 된다.
그럼 이제는 직관적인 설명보다는 수식을 통해 설명하겠다.
아래의 증명과정은 위의 동영상의 내용을 참고했다.
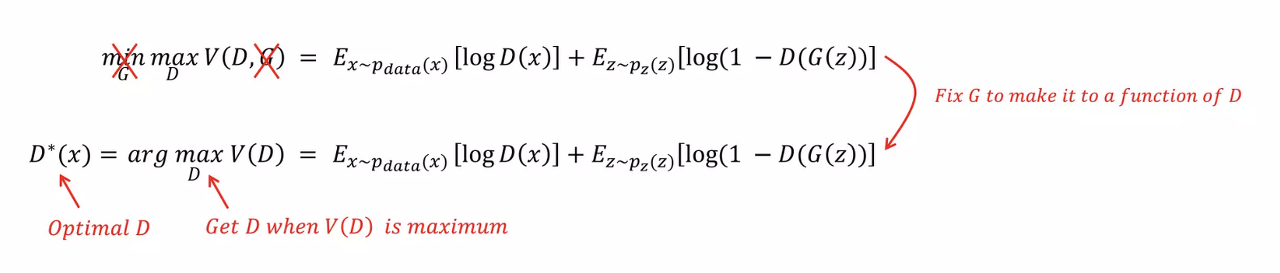
1. 임의의 Generator에 대해 Optimal Discriminator $D_{G}^*(x)$를 찾는 것이므로,
최적의$G$가 주어졌다고 보고 $G$를 식에서 지울 수 있고, 이에 따라 $D$의 식으로 고칠 수 있다.
($G$는 고정했으므로, Variant한 모든 식에서 제외가능)
Optimal Discriminator 상태에 도달했다는 것은 Generator 관점에서 봤을 때,
이미 $p_{data} = p_{g}$ 상태로 학습이 거의 다 됐다는 것을 의미한다.
즉, $G$가 이미 최상의 상태에 도달했다고 가정하여 $G$를 fix 시키고 optimal Discriminator $D_{G}^*(x)$에 대한 수식만 찾는 것이다.

2. 두 번째 식에서는 noise $z$를 sampling하여 Generator가 image space로 mapping한 것을 $x = G(z)$라고 한다면,
noise 분포 $p_{z}$에서 $z$를 sampling한 것에서 Generator가 Mapping한 Fake image의 분포 $p_{g}$에서 $x$를 sampling한 것으로 볼 수 있다.
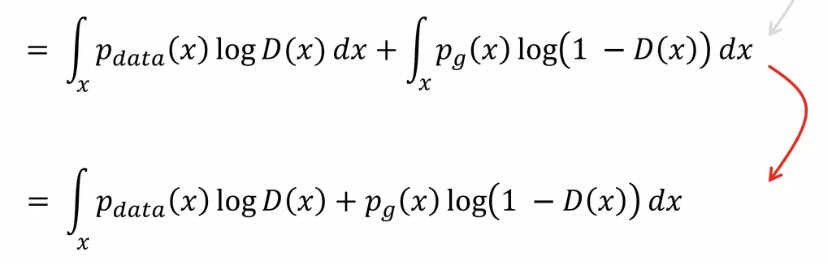
3. 위의 식을 Expectation (Continuous RV)에 대한 식으로 바꾸면 위의 식으로 정리가 가능하다.
$E_{x \sim p(x) }\left [ f(X) \right ] = \sum f(x)p_{X}(x) = \int_{x}^{}p(x)f(x)dx $
$\sum (변수 \times \: 확률)$ or $\int_{x} (변수 \times 확률)dx $
변수는 합성 form 그대로
확률은 Main(원본) 변수의 확률

4. 위 식에서 max가 되는 $D_{G}^*(x)$를 찾아야 하는데, 결국 integral 안의 값을 maximize 하면 되므로 integral 안의 식만 보자.
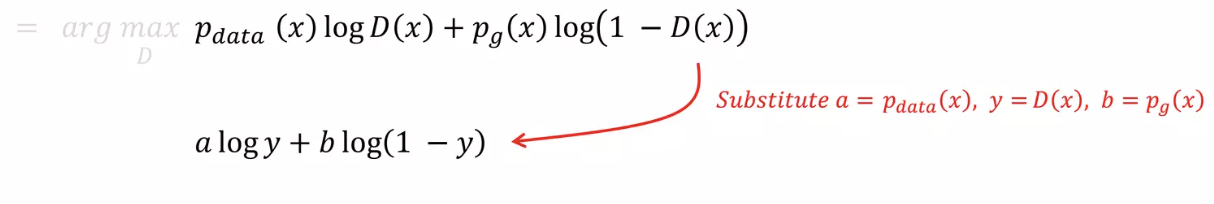
5. 위의 식을 최소로 하는 $D(x)$를 찾아야 하므로, 위 식을 $D(x)$에 대해 partial differentiation(편미분)하자.
이때, $a = p_{data}(x), y = D(x), b = p_{g}(x)$로 치환하면 보기 편하다.

6. 위의 식을 치환하여 미분해서 부호가 바뀌는 점을 찾으면 결국 $arg \max_{D}V(D) = D_{G}^*(x)$인 $D$를 찾을 수 있다.

결국 구해보면 $D_{G}^*(x) = \frac{P_{\text{data}}(x)}{P_{\text{data}}(x) + P_g(x)}$ 이라는 것을 알 수 있고,
$(a, b) \in \mathbb{R}^2 \setminus \{(0, 0)\}$: $(a, b) = (0, 0)$을 제외한 차집합
만약 $(0, 0)$을 포함하면 $\frac {a} {a+b}$에서 분모가 0이 될 수 있기 때문이다.
7. 지금까지 $D$는 $D_{G}^*(x) = \frac{P_{\text{data}}(x)}{P_{\text{data}}(x) + P_g(x)}$에서 Global Optimum을 갖는다는 것이 증명됐다.

그럼 결과적으로 왜 $a = b, p_{g} = p_{data}$일 때 Global Optimum을 갖고 그 값이 $\frac {1} {2}$인지 증명해야 한다.
Theorem 1
임의의 $G$에 대한 Optimal $D$는 $D_{G}^*(x) = \frac{P_{\text{data}}(x)}{P_{\text{data}}(x) + P_g(x)}$이므로, 이 식을 아래의 식에 대입하자.
$\min_{G} \max_{D} V(D, G) = \min_{G} V(D^*, G)$이고, $G$의 최소값은 $D$가 global optimal을 가질 때($D_{G}^*(x)$)이다.
$V(D^*, G) = \mathbb{E}_{x \sim p_{\text{data}}}[\log D^*(x)] + \mathbb{E}_{x \sim p_{g}}[\log(1 - D^*(x))]$
$= \int_{x} p_{\text{data}}(x) \log \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_{g}(x)} \, dx + \int_{x} p_{g}(x) \log \frac{p_{g}(x)}{p_{\text{data}}(x) + p_{g}(x)} \,$
여기서 약간의 trick을 사용한다. $\log4$를 더하고 빼서 우리가 원하는 KL-Divergence의 형태로 만들어준다.
$ = -\log 4 + \log 4 + \int_{x} p_{\text{data}}(x) \log \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_{g}(x)} \, dx + \int_{x} p_{g}(x) \log \frac{p_{g}(x)}{p_{\text{data}}(x) + p_{g}(x)} \, dx $
$ = -\log 4 + \int_{x} p_{\text{data}}(x) \log 2 \cdot \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_{g}(x)} \, dx + \int_{x} p_{g}(x) \log 2 \cdot \frac{p_{g}(x)}{p_{\text{data}}(x) + p_{g}(x)} \, dx $
여기서 2를 분모, 분자 모두 나눠주면 우리가 원하던 KL - Divergence의 형태로 식변형이 가능하다.
$ = -\log 4 + \text{KL}\left(p_{\text{data}} \middle\| \frac{p_{\text{data}} + p_{g}}{2} \right) + \text{KL}\left(p_{g} \middle\| \frac{p_{\text{data}} + p_{g}}{2} \right) $
JS(Jensen-Shannon) Divergence는 KLD가 결국 두 분포의 '차이'를 나타낼 뿐, '거리'를 나타낼 수 없다는 한계에서 나왔다.
즉, JSD를 사용하면 두 분포의 '거리'를 나타낼 수 있음과
동시에 '거리'라는 의미를 지니고 있으므로 항상 양수이다.
$ = -\log 4 + 2 \cdot \text{JSD}(p_{\text{data}} \| p_{g})$
즉, 여기서 $\min_{G} V(D^*, G)$를 최소화하는 $G$는 $D = D_{G}^*(x)$일 때이고,
$p_{data} = p_{g}$로 두 분포가 동일할 때 $\min_{G} V(D^*, G) = -\log 4$로 global minumum을 갖는다.

Cross - Entropy
$Cross \: Entropy = -\sum_{i=1}^{n} y_{i}log \hat{y}_{i}$
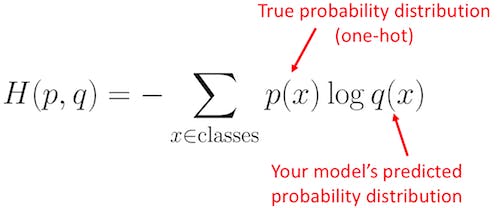
CEE는 분포간의 차이에 집중하고, 분류 문제에서 정답 Label에 One-Hot Encoding을 했을 때만 사용한다.
ML/DL Model은 실제로 존재하는 어떤 분포를 잘 묘사해주는 확률 모델을 구하는 것과 같다.
- 정답 분포가 신경망으로 구성된 분포인가에 상관없이 신경망을 이용해서 해당 분포를 묘사할 수 있다고 생각한다
- 보편 근사 정리(Universal approximation Theorem): 하나의 Hidden Layer를 갖는 ANN은 임의의 연속인 다변수 함수를 원하는 정도의 정확도로 근사할 수 있다

Kullback - Lively Divergence (KLD)
$ D_{KL}(p\parallel q) = \sum_{x}^{}p(x)log\frac{p(x)}{q(x)} = E_{x\sim p}\left [ log \frac{p(x)}{q(x)} \right ]$
- 모델로 만든 분포 q와 실제 분포 p 사이에서 분포간의 차이를 나타낼 때 사용
- x가 실제 분포 P를 따른다: $x \sim p$

CE with Distribution (분포 p,q)
$ D_{KL}(p\parallel q) = \sum_{x}^{}p(x)log\frac{p(x)}{q(x)}$
$= \sum_{x}^{}p(x)logp(x) - \sum_{x}^{}p(x)logq(x) = -H(p) + CE(p,q) = CE(p,q)$
$\therefore D_{KL}(p\parallel q) = CE(p,q)$
- 식 변형을 하면 KL Divergence는 p, q의 Cross - Entropy에서 p의 Entropy를 뺀 값
- 그런데 Classification Problem의 경우 p는 실제 값(고정값 하나)를 갖기 때문에 p의 Entropy $H(p) = 0$가 됨 ($p(x) = 1$)
- 따라서, Classfication Problem의 경우 $D_{KL}(p\parallel q) =CE(p,q)$
정리하자면, 앞서 언급했던 질문인 "설계한 Deep Learning(Probability) Model이 Global Optimum을 갖는가?"에 대해,
$p_{data} = p_{g}$일 때, $C(G) = - \log (4)$로 "Global Optimum을 갖는다"고 할 수 있다.
4.2) Convergence of Algorithm 1
설계한 Deep Learning(Probability) Model이 Global Optimum에 수렴하는가?
해당 파트는 결국 이 모델을 만드는 이유인 Generator가 real image의 확률 분포로 수렴할 수 있는가에 대해 증명을 한다.
즉, $p_{g}$가 $p_{data}$로 수렴할 수 있는가 = Generator의 관점에서 $p_{g}$의 loss function이 global optimum으로 convergence할 수 있는지를 따져야 한다.
이를 판별하기 위해서는 "$D$를 고정시키고, loss function이 convex 한지 확인" 해야 한다.
$D$는 고정했기 때문에, $U(p_{g}, D)$를 $p_{g}$의 관점에서 보면 $D$는 고정된 상수값이다.
즉, $p_{g}$ 관점에서 $U(P_{g}, D)$의 변수는 $P_{g}$ 이고, 결국 $P_{g}$가 학습함에 따라 변하는데
변하는 $P_{g}$에 따라서 $U(P_{g}, D)$가 convex한지 알아봐야 iterative optimization (e.g. gradient descent) 방식으로 Global Optimum을 찾을 수 있는지 확인할 수 있다.
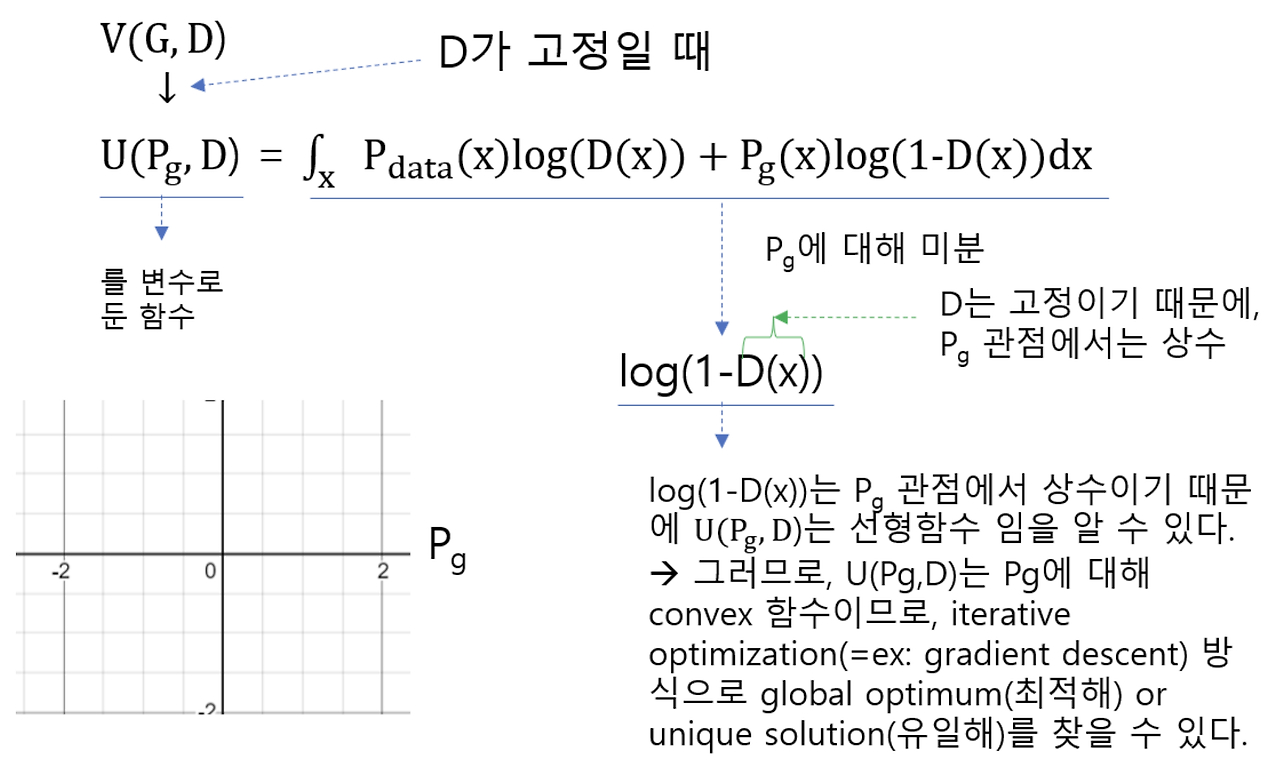
$U(p_{g}, D) = \int_{x} P_{\text{data}}(x)\log(D(x)) + P_{g}(x)\log(1 - D(x)) \, dx$ 안의 식을 $p_{g}$에 대해 미분하면
$\log(1-D(x))$가 나오는데, $p_{g}$의 관점에서는 상수이므로 상수를 적분한 $U(p_{g}, D)$는 선형함수이다.
선형함수는 convex하므로, 특정 구간을 지정해놓으면 해당 구간에서 minimum(global optimum or unique solution)을 찾을 수 있다.

Convex Function의 모든 Gradient에는 $D^*$에 해당하는 Gradient 또한 포함된다는 뜻이다.
즉, Convex 함수에 Optimal Global이 존재한다는 것을 증명했으므로 자명하다.
4.3) Algorithm 1
설계한 Deep Learning(Probability) Model이 Global Optimum을 찾을 수 있는 Algorithm이 존재하는가?

논문에서는 위와 같은 방식으로 Discriminator를 k-step, Generator를 1-step으로 번갈아 학습함으로써
Global Optimum을 찾을 수 있음을 보여주었다.
4.4) Neural Networks on Generative Model
GAN은 Generator가 생성하는 데이터의 분포 $p_{g}$를 optimize하는 것이 아니라,
$p_{g}$를 생성하는데 직접적인 영향을 미치는 parameter인 $\theta_{g}$를 추정하고 최적화한다.
또한, Generative Model이나 Discriminative Model이 Neural Network를 사용한다는 수학적인 증명은 없다.
그렇기에 Generative Model을 MLP와 같은 것을 설계하게 되면 실제로 최종 Loss Function 자체가 Convex 하지 않을 수 있고, 이는 multiple critical points를 가질 수 있다는 문제가 있다.
그러나, 막상 이러한 theoretical guarantees가 보장되지 않고도 실제 사용환경에서는 MLP를 사용해도 Generative Model에서 나름 잘 작동한다.
References
0. Abstract
해당 논문에서는 두 가지의 Model(Discriminator, Generator)을 Adversarial Process를 통해 동시에 훈련하는 Generative Model의 아이디어를 제안한다.
Discriminator(판별자)는 Generator가 만든 Fake Data가 아닌 Real Data의 확률분포를 추정하고, Generator(생성자)는 임의의 Noise를 Sampling하여 Real Data와 유사한 분포를 Mapping(생성)한다.
이때, Generator는 Discriminator가 자신이 만든 Fake Data를 Real Data로 착각하도록 하는 확률을 최대화하도록 한다.
이러한 학습 구조를
minimax two-player game
이라 한다.
나중에 보면 알겠지만,으로 Value Function을 정의하기에
Generator는 Value를 Minimize 시켜야 하고, Discriminator는 Value를 Maximize 시켜야 한다.

임의의 Discriminator와 Generator에 대하여 unique solution이 존재한다면
Generator는 Real Data(Training Data)의 Probability Distribution을 완벽하게 복원하는 것이고
Discriminator는 임의의 Input Data에 대한 정답확률을 항상
Discriminator가의 정답 확률을 갖는 이유는
Generator가 real data의 확률분포를 완벽하게 복원하게 된다면
Discriminator는 들어온 input에 대하여 real인지 fake인지 구별할 수 없게 된다.
즉, Random하게 맞거나 틀리게 되므로 항상의 확률을 갖는다.
논문에서는 G와 D 모두 MLP(Multi-Layer Perceptron)으로 구성되어 있기에 backpropagation을 통해 훈련이 가능하다고 말한다.
즉, Markov chains 이나 Unrolled approximate inference networks가 이제 필요하지 않다고 주장한다.
이렇게 주장을 하는 이유는 GAN 이전의 Generative Model의 발전 흐름이
Markov chains 이나 Unrolled approximate inference networks를 사용했기 때문이다.
위의 내용들을 반영한 이전의 Generative Model들은 VAE(Variational AutoEncoders), Restricted Boltzmann Machines 들이 있다.
In Ian Goodfellow et al's paper "Generative Adversarial Networks", why do they specify that they do not need a Markov chain or i
In Ian Goodfellow et al's paper Generative Adversarial Networks, they state, "There is no need for any Markov chains or unrolled approximate inference networks during either training or generation of
stats.stackexchange.com

1. Introduction
GAN 이전의 Deep Learning이 작동하는 방식은 각 Input data의 종류(natural images, audio waveforms, etc.)에 맞춰 모집단에 근사하는 Probability Distribution을 나타내는 rich, hierarchical(다양한, 계층적) Model을 찾는 것이었다
따라서, Discriminative Model의 경우 고차원의 정제된 데이터를 Class Label에 1:1 Mapping 하여 구분하는 모델을 사용했다.
well-behaved gradient를 부분적으로 갖는 선형 활성화 함수(ReLU)들을 사용했고,
이들을 기반으로 한 Backpropagation, Dropout 알고리즘들에 기반했다.
이에 비해 Deep Generative Model들은 크게 2가지의 어려움이 있었다.
- Maximum likelihood estimation과 관련된 전략들에서 발생하는 많은 확률 연산들을 근사하는데 발생하는 어려움
- Generative Context에서는 앞선 Discriminative Model의 성공을 이끌었던 선형 활성화 함수들의 이점을 사용하는데 어려움
difficulty of approximating many intractable probabilistic computations 에서
"intractable computation"은 컴퓨터로 할 수 없는 계산을 의미한다.
즉, 컴퓨터로 계산할 수 없는 확률을 보통 계산할 수 있도록 근사를 해서 푸는데, 이것 마저 어렵다는 뜻이다.
여기서 intractable의 기준은 다항시간 내에 풀 수 없는 문제를 의미하는데(intratable, NP Problem), 3차 이상의 시간복잡도를 갖는 알고리즘을이라 한다.
결과적으로 기존의 Generative Model들은 컴퓨터로 계산할 수 없는 intractable computation 과정을 근사하여 푸는 것 조차 어려웠기 때문에 성장하지 못했다는 뜻이다.
결국 논문에서는 이러한 한계점들을 극복하지 않고, 회피하여 새로운 Generative Model을 제안한다.
제안된 구조는 Adversarial nets framework로, Generative Model이 Discriminative Model과 서로 경쟁하는 구조이다.
Discriminative Model은 주어진 sample data가 Generative Model이 생성한 Fake Data인지, 아니면 Training Data인 Real Data인지 구별하는 것을 학습한다.
sample from the model distribution: Fake Data
sample from the data distribution: Real Data

위의 내용을 더 간단히 설명하기 위해 너무나 유명한 예시를 가져왔다.
GAN의 경쟁 과정을 경찰(Discriminator)과 위조지폐범(Generator) 사이의 경쟁으로 바라보자.
위조지폐범은 최대한 실제 화폐와 비슷한 화폐를 만들어, 경찰을 속이기 위해 노력한다. 경찰은 진짜 화폐와 위조지폐범이 만든 가짜 화폐를 완벽하게 구분하여 위조지폐범을 검거하는 것을 목표로 삼는다.
따라서, 위의 과정을 반복하다 보면 다음과 같은 순간에 도달한다.
위조지폐범이 진짜와 다를 바 없는 위조지폐를 만들게 되고, 그 결과 경찰은 실제 지폐와 위조 지폐간의 차이를 구분할 수 없고 위조지폐를 구별할 수 있는 확률이 50%에 수렴하게 된다.
즉, GAN의 목적은 각각의 역할을 가진 Discriminator와 Generator를 이용하여 Real Data의 확률분포를 따르는 Fake Data를 생성해내는 능력을 키워주는 것이라 할 수 있다.
이러한 Framework는 많은 training algorithm과 다양한 종류의 model, optimization algorithm들을 사용할 수 있다.
특히나 special한 case인 Generator와 Discriminator 모두 MLP(Multi-Layer Perceptron)를 사용할 경우 저자들은 이를 'adversarial nets'라 한다.
Adversarial Nets의 경우
1. Discriminator와 Generator 모두를 highly successful한 backpropagtion과 dropout algorithm 으로 학습이 가능하다.
2. Generator가 only foward propagation을 통해 noise로부터 sampling이 가능하다.
2. Related Work
Related Work 부분에서는 이전까지 수행됐던 Generative Model에 관한 Review가 진행된다.
Boltzmann Machine, Restricted Boltzmann Machine, Variational AutoEncoders(VAE) 등은 추후에 해당 분야에 대해 학습을 마친 후 작성하도록 하겠다.
VAE에서 사용한 variational inference (approximate inference) 기법이나,
Traditional Generative Model에서 사용된 Markov Chains 등을 사용하지 않아도 된다는 점이 GAN의 큰 장점이다.
3. Adversarial nets
Discriminator, Generator 모두가 MLP(Multi-layer perceptron) 구조일 때, Adversarial Modeling Framework를 적용하기가 가장 용이하다.
3.1) Value Function
Data
그리고 noise
는 라는 noise를 sampling하여 Data Space에 분포를 Mapping 해주는 역할을 한다.
예시를 들기 위해, 1과 2만 있는 MNIST Dataset을 생각해보자.
다음과 같이 784(28*28)개의 pixel을 Data Space에 나타난다고 했을 때,
위의 그림처럼 나오면 2, 아래의 그림처럼 나오면 1로 성공적으로 Mapping이 되었다고 볼 수 있다.
처음에는 Mapping시 원하는 Domain 안으로 Mapping 되지 않지만,
학습이 진행될수록 Generator의 Mapping이 원하는 Domain 안으로 떨어지는 것을 볼 수 있다.


MLP로 이루어진

1. noise 분포
2. noise를 G에 input으로 넣는다. G는
3.
4. G는
는 가 에서 나온 fake image를 구별하는 과정이다.
따라서의 입장에서는 자신이 만든 fake image가 는 구별할 수 없도록,
real image label인 1을 scalar로 반환하도록 만들어야 한다.
즉,로 Minimize 되도록 가 노력하는 것이다.
일단 용어부터 먼저 정리하자.
: 가 를 , 즉 real data로부터 가지고 있다고 판단할 확률의 기댓값이다
: 가 , 즉 noise를 통해 생성한 fake data를 fake data로 판단할 확률의 기댓값이다
Discriminator의 관점
따라서 Discriminator는 기댓값을 Maximize,

Generator의 관점
Generator는 기댓값을 Minimize, 즉

3.2) GAN Training Process
(a) 초반에는 noise
다만 초기 step에서는 해당 Mapping(Green)이 원래 이미지의 분포(Black)와 다르다.
uniform distribution을 따르는는 으로의 Mapping을 통해 non-uniform distribution이 적용된다.

Q1. Input Noise
A. 가능하다. GAN 방식 자체가
Generative Model의 목적은 image data의 확률 분포를 maximum likelihood 하기를 원한다.
하지만 image data의 확률 분포를 한 번에 아는 것은 쉽지 않기 때문에 Training을 통해 Generative Model을 image data의 확률 분포에 maximum likelihood 하도록 estimation (추정) 하는 것이다. 이렇게 추정을 하는 방식은 아래와 같이 두 가지로 나뉜다.

첫 번째 방식은 Explicit density이다. 예를 들어, VAE에서는 image data의 확률 분포
즉, 이상적인 noise
그렇기 때문에 VAE 모델은 사전에 명시적(explicit)으로
특히 VAE에서 초기에 설정한 density estimation 수식은 intractable 했기 때문에 이를 variational inference를 이용해 approximation하도록 하여 tractable 하게 바꾸게 된다.

두 번째 방식은 GAN과 같은 implicit density 방식이다.
앞서 언급한 VAE처럼 Explicit density(명시된 사전 확률분포)를 이용하는 것이 아니라 사전에 어떠한 확률 분포도 명시하지 않는다.
즉, noise
따라서 앞서 input noise인를 sampling할 때, 가 uniform distribution을 따른다는 가정하에 sampling을 해도 되고
gaussian distribution을 따른다는 가정하에 sampling을 해도 되는 것이다.
정리하면 GAN 방식을 이용한 Generative Model은 input noise
Since an adversarial learning method is adopted, we need not care about approximating intractable density functions.
앞의 VAE에서 intractable 하다고 했던 이유는 사전에 explicit하게 정의된 input noise의 probability distribution(=density function)때문이라고 했는데,
GAN에서는 input noise의 probability distribution에 대한 제약이 없기 때문에 애초에 intractable density function을 approximate할 필요가 없게 된다.
(b) Generator의 가중치를 Freeze(고정)하고, Discriminator를 학습한다.
Real Image에 대해 안정적으로 1에 가까운 확률, Fake Image에 대해 안정적으로 0에 가까운 확률을 반환하도록 학습한다.
그림을 보면인 Discriminator 분포가 (a)에 대해 안정적인 형태를 띄고 있음을 알 수 있다.

(c) Discriminator를 Freeze(고정)시키고, Generator를 학습한다.

(d) Training을 여러 번 완료한 후에, G와 D가 둘다 enough capacity가 있다면
그에 따라 Discriminator 또한 real data와 Generator가 생성한 fake data 사이를 구별하지 못하기 때문에,
그냥 random에 의한 동전 던지기로
실제 Blue, dashed line을 보면 딱 절반만큼의 확률인로 수렴한 것을 볼 수 있다.

또한 training loop 안에서
3.3) Non - Saturating Game
저자들은 위의 Training Process에서 하나의 문제점을 지적한다.
그것은 바로 Generator가 학습 초반에 real data의 분포와는 전혀 다른 분포를 갖게 된다는 점이다.
그에 따라 Discriminator는 높은 confidence score를 가지고 매우 쉽게 real image와 Generator가 생성한 조잡한 fake image를 구별할 수 있게 되고, 이는 학습이 제대로 진행되지 않는 문제를 야기한다.

학습이 제대로 진행되지 않는 이유는, update되는 Gradient 값이 saturation된 상태이기 때문에 update가 매우 느리기 때문이다.
초반에는 Generator가 정교하지 않은 조잡한 fake image를 생성하므로 Discriminator가로 생성된 이미지를 Fake라고 잘 판별하게 된다. ( )
그런데,꼴의 함수에서 초기 의 값이 0이 나온다면 gradient 값 자체가 saturation된 상태이기 때문에 update가 더딜 수 있다.
그렇기에 Generator를 학습시키는 관점을를 Minimize 하는 것이 아니라, 를 Maximize하는 방향으로 변경한다.
이러한 문제점을 해결하기 위해 Generator의 학습방향을

어차피 Generator의 입장에서는이 되도록 G를 학습시키기만 하면 되기 때문에 를 Minimize 한다 = 를 Maximize 한다 = 을 반환하도록 한다
위의 세 개는 전부 같은 말이므로, 실제 학습이 사용되는 Value Function의 Term을 바꿔도 문제없다.
즉, 실제 학습에 사용되는 Value Function
위의 practical usage를 보면 Binary - Cross Entropy Loss를 사용한다.
여기서 Generator를 훈련시킬 때 Discriminator가 fake image(0)에 대해 real image(1)로 착각하게끔 해야 하므로라는 value에 대해 label = 1로 설정해야 한다.
그 결과에 를 대입하면 되므로 가 된다.
결국 BCELoss를 사용하면 Generator를 훈련시킬 때 알아서 Non-Saturate되도록 Loss Function이 설정된다.
4. Theoretical Results
Generator
즉 충분한 capacity와 training time이 있다면 Generator가 생성한 Fake image의 분포
아래에 설명된 Algorithm1은 설계한 Deep Learning Model의 Global Optimum을 찾는 Algorithm이다.

Deep Learning Model을 설계할 때에는 아래의 4가지 기준을 만족했는지 살펴봐야 한다.
물론 더 많은 기준이 있을 수 있겠으나, GAN 논문에서는 아래 4가지 정도로 요약했다.
또한 뒤에서 나오지만, 실제 Neural Network가 사용되면 아래의 기준을 이상적으로 만족하는 것이 불가능하다. 따라서 아래의 기준들은 DL Model 설계시 지향해야 하는 이상적인 Guideline 정도로 생각하면 된다.
1. 설계한 Deep Learning(Probability) Model이 Tractable 한가? (계산 시스템 관점에서 충분히 다룰 수 있는 알고리즘인가?)
2. 설계한 Deep Learning(Probability) Model이 Global Optimum을 갖는가?
3. 설계한 Deep Learning(Probability) Model이 Global Optimum에 수렴하는가?
4. 설계한 Deep Learning(Probability) Model이 Global Optimum을 찾을 수 있는 Algorithm이 존재하는가?
4.1) Global Optimality of
설계한 Deep Learning(Probability) Model이 Global Optimum을 갖는가?
GAN의 최종 Value Function은 어떠한 값을 가져야 Global Optimum이라 할 수 있는가?
즉, 최종적으로 도달하고자 하는 loss 값은 무엇인가?
Generator 관점에서 MinMax problem (value function)은
직관적으로 봤을 때, Generator가 생성하는 fake data의 distribution인가
real data의 distribution인와 유사한 distribution을 형성하는 지점인 곳에서
global optimum 값을 찾게 되면 학습을 중단한다.
논문에서는 임의의 Generator에 대한 Optimal Discriminator의 global optimum 값은 다음 수식에 의해 도출된다고 설명한다.
위 수식의 직관적인 설명은 다음과 같은데,
즉, 진짜와 가짜를 구별할 능력이 없기에 그냥 랜덤하게 절반의 확률로 판별한다는 것이다.
그러므로 GAN의 Loss Function인에서 에 수렴한다면 학습을 종료하면 된다.
그럼 이제는 직관적인 설명보다는 수식을 통해 설명하겠다.
아래의 증명과정은 위의 동영상의 내용을 참고했다.
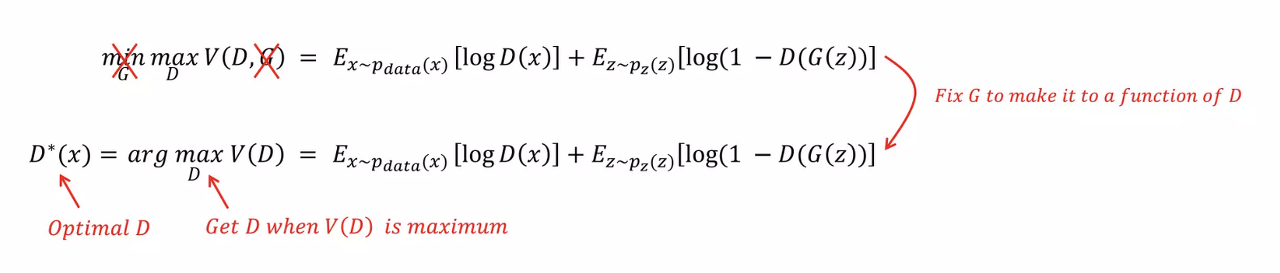
1. 임의의 Generator에 대해 Optimal Discriminator
최적의
(
Optimal Discriminator 상태에 도달했다는 것은 Generator 관점에서 봤을 때,
이미상태로 학습이 거의 다 됐다는 것을 의미한다.
즉,가 이미 최상의 상태에 도달했다고 가정하여 를 fix 시키고 optimal Discriminator 에 대한 수식만 찾는 것이다.

2. 두 번째 식에서는 noise
noise 분포
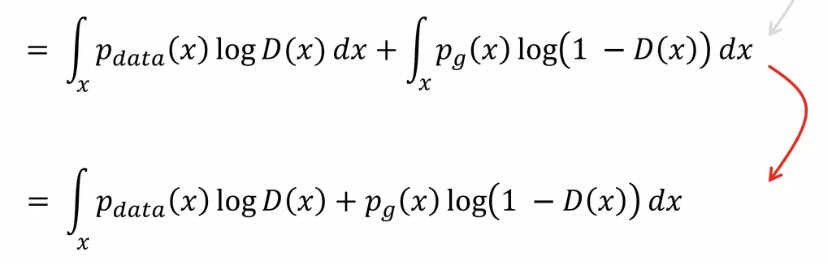
3. 위의 식을 Expectation (Continuous RV)에 대한 식으로 바꾸면 위의 식으로 정리가 가능하다.
or
변수는 합성 form 그대로
확률은 Main(원본) 변수의 확률

4. 위 식에서 max가 되는
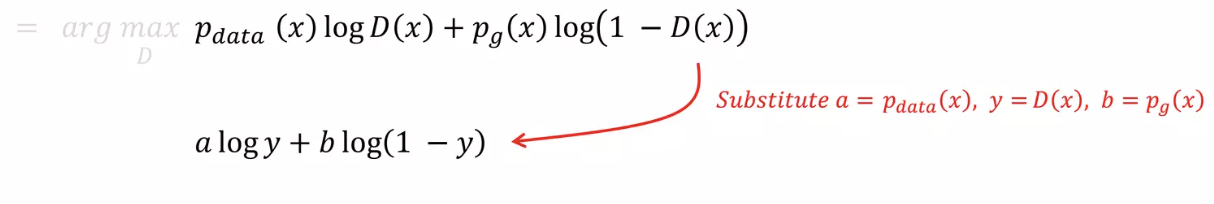
5. 위의 식을 최소로 하는
이때,

6. 위의 식을 치환하여 미분해서 부호가 바뀌는 점을 찾으면 결국

결국 구해보면
: 을 제외한 차집합
만약을 포함하면 에서 분모가 0이 될 수 있기 때문이다.
7. 지금까지

그럼 결과적으로 왜
Theorem 1
임의의
여기서 약간의 trick을 사용한다.
여기서 2를 분모, 분자 모두 나눠주면 우리가 원하던 KL - Divergence의 형태로 식변형이 가능하다.
JS(Jensen-Shannon) Divergence는 KLD가 결국 두 분포의 '차이'를 나타낼 뿐, '거리'를 나타낼 수 없다는 한계에서 나왔다.
즉, JSD를 사용하면 두 분포의 '거리'를 나타낼 수 있음과
동시에 '거리'라는 의미를 지니고 있으므로 항상 양수이다.
즉, 여기서

Cross - Entropy

CEE는 분포간의 차이에 집중하고, 분류 문제에서 정답 Label에 One-Hot Encoding을 했을 때만 사용한다.
ML/DL Model은 실제로 존재하는 어떤 분포를 잘 묘사해주는 확률 모델을 구하는 것과 같다.
- 정답 분포가 신경망으로 구성된 분포인가에 상관없이 신경망을 이용해서 해당 분포를 묘사할 수 있다고 생각한다
- 보편 근사 정리(Universal approximation Theorem): 하나의 Hidden Layer를 갖는 ANN은 임의의 연속인 다변수 함수를 원하는 정도의 정확도로 근사할 수 있다

Kullback - Lively Divergence (KLD)
- 모델로 만든 분포 q와 실제 분포 p 사이에서 분포간의 차이를 나타낼 때 사용
- x가 실제 분포 P를 따른다:

CE with Distribution (분포 p,q)
- 식 변형을 하면 KL Divergence는 p, q의 Cross - Entropy에서 p의 Entropy를 뺀 값
- 그런데 Classification Problem의 경우 p는 실제 값(고정값 하나)를 갖기 때문에 p의 Entropy
- 따라서, Classfication Problem의 경우
정리하자면, 앞서 언급했던 질문인 "설계한 Deep Learning(Probability) Model이 Global Optimum을 갖는가?"에 대해,
4.2) Convergence of Algorithm 1
설계한 Deep Learning(Probability) Model이 Global Optimum에 수렴하는가?
해당 파트는 결국 이 모델을 만드는 이유인 Generator가 real image의 확률 분포로 수렴할 수 있는가에 대해 증명을 한다.
즉,
이를 판별하기 위해서는 "
즉,
변하는

선형함수는 convex하므로, 특정 구간을 지정해놓으면 해당 구간에서 minimum(global optimum or unique solution)을 찾을 수 있다.

Convex Function의 모든 Gradient에는
즉, Convex 함수에 Optimal Global이 존재한다는 것을 증명했으므로 자명하다.
4.3) Algorithm 1
설계한 Deep Learning(Probability) Model이 Global Optimum을 찾을 수 있는 Algorithm이 존재하는가?

논문에서는 위와 같은 방식으로 Discriminator를 k-step, Generator를 1-step으로 번갈아 학습함으로써
Global Optimum을 찾을 수 있음을 보여주었다.
4.4) Neural Networks on Generative Model
GAN은 Generator가 생성하는 데이터의 분포
또한, Generative Model이나 Discriminative Model이 Neural Network를 사용한다는 수학적인 증명은 없다.
그렇기에 Generative Model을 MLP와 같은 것을 설계하게 되면 실제로 최종 Loss Function 자체가 Convex 하지 않을 수 있고, 이는 multiple critical points를 가질 수 있다는 문제가 있다.
그러나, 막상 이러한 theoretical guarantees가 보장되지 않고도 실제 사용환경에서는 MLP를 사용해도 Generative Model에서 나름 잘 작동한다.
References
