[AI DEEP DIVE] Chapter 9.1: RNN (Recurrent Neural Network, RNN Backpropagation, plain RNN)

https://fastcampus.co.kr/data_online_aideep

혁펜하임의 AI DEEP DIVE (Online.) | 패스트캠퍼스

 

 

 

---

1. RNN (Recurrent Neural Network)

 

     

 

Background 

 

• 자연어라는 data가 특정한 순서를 가지고 들어오는 입력 data라는 것에 착안하여, sequence data(순서가 있는 연속적인 데이터)를 처리할 수 있는 핵심요소
• RNN을 기반으로 입력, 출력이 sequence로 주어지는 Seq2Seq라는 Task
• 그에 대한 special case인 language modeling task까지 자연어 처리를 중심으로 함

 

 

 

 

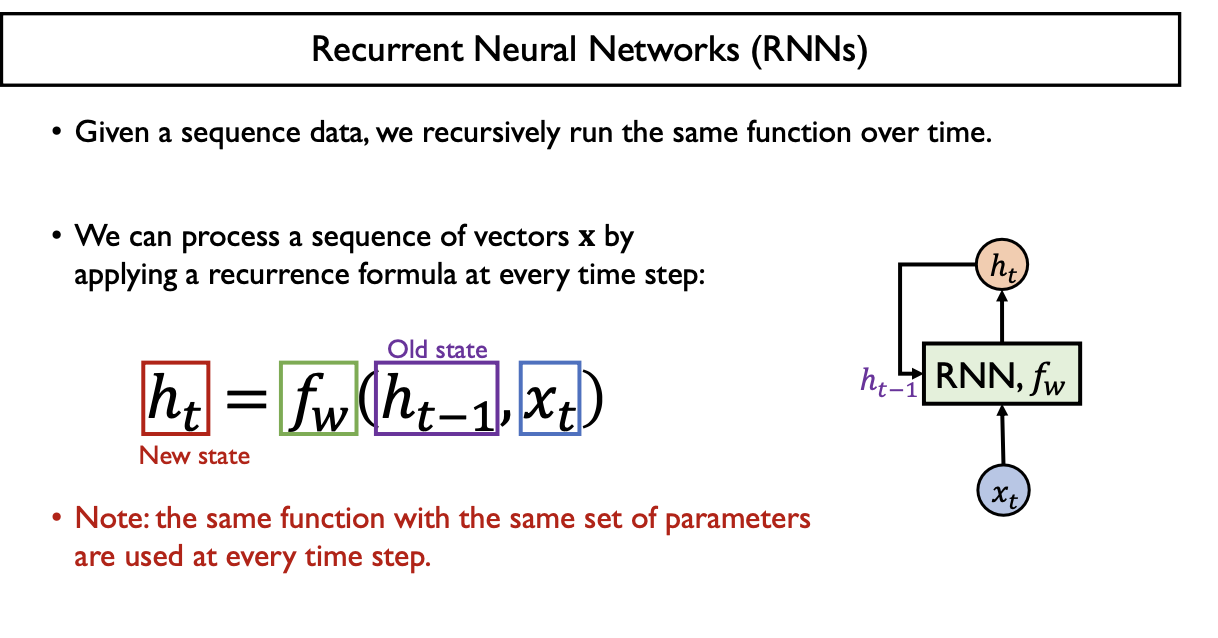
 RNN

 

• Sequence Data (순서가 있는 연속적인 데이터) 처리에 특화된 기술
• 이전 정보를 반영 (hidden state vector가 이전 정보를 담는 역할)

 

 

 

• RNN이라는 동일한 Function을 반복적으로 호출
• $X_{t}$ : 특정 time step $t$에서의 input vector
• $h_{t-1}$ : 이전 time step $t-1$에서의 동일한 RNN Function이 계산했던 hidden state vector
• $f_{W}$ : $h_{t-1}, X_{t}$ 두 개를 입력으로 받아서 현재의 time step $t$에 RNN Modue의 output인 $h_{t}$인 current hidden state vector를 만들어주게 됨

 

 

• $W_{hh}$: 이전 time step $t-1$ 에서의 hidden state vector $h_{t-1}$ 에서 현재 time step $t$에서의 hidden state vector $h_{t}$로 mapping하는 weight matrix
• $W_{xh}$: 현재 time step $t$ 에서의 input vector $x_{t}$에서 현재 time step $t$ 에서의 hidden state vector $h_{t}$로 mapping하는 weight matrix
• $W_{hy}$: 현재 time step $t$에서의 hidden state vector $h_{t}$에서 output layer로 mapping하는 weight matrix

 

 

 

매 time step 마다 동일한 function $f_ {w}$ 가 반복적으로 수행된다.

 

 

 

$h_{t} = tanh(x_{t}W_{xh} + h_{t-1}W_{hh} + b)$

 

 

 

즉, 동일한 Parameter set을 지닌 Layer가 반복적으로 수행되기 때문에 함수 $f_{w}$의

 

 

 

Parameter가 모두 time-invariant 하다는 것을 의미한다.

 

 

 

$W_{xh}, W_{hh}, b, b_{y}$는 시간에 따라 다르지 않기 때문에 임의의 time step $t$에서의

 

 

 

$W_{xh}, W_{hh}, b, b_{y}$ 는 모두 동일하다. (상수로 취급)

 

 

 

 

 

여러 time step 동안에 특정 time step에서 prediction을 해야 하는 경우

 

 

 

 

$ \hat{y}_{t} = h_{t}W_{hy} + b_{y}$

 

 

 

현재 time step $t$의 hidden state vector $h_{t}$를

 

 

 

다시 입력으로 output layer $y_{t}$에 전달해 줌으로써 최종 예측 결과를 생성한다.

 

 

 

 

 

특정 time step t에서의 prediction 하는 경우 h_t를 output layer에 input으로 전달

 

 

 

 

Input vector & 이전 time step의 hidden state vector 각각 fully-connected layer를 통과해서

(model parameter와 input feature간의 linear combination)

 

 

 

output vector $W_{hh}h_{t-1}, W_{xh}x_{t}$를 각각 생성한다.

 

 

 

이후 두 개의 output vector와 Bias를 합산해서 중간결과물을 만들고 이를 activation function $tanh$ 에 합성시켜 현재 time step의 hidden state vector $h_{t}$ 생성한다.

 

 

 

이때, $h_{t}$와 $h_{t-1}$의 차원이 동일하게끔 matrix $W_{hh}, W_{xh}$의 size를 조정

 

• 그래야만 그 다음 time step의 '이전 time step의 hidden state vector' 자리에 들어가기 때문
• 연쇄적으로 hidden state vector가 동일한 차원을 지닌 상태로 들어간다

 

 

 

특정 time step t에서 어떤 output을 predict 하기 위해서는 hidden state vector를 output layer 가 입력으로 받아서 $W_{hy}h_{t}$ 선형변환을 통해 최종 output vector $\hat{y}_{t}$를 반환

 

 

 

• Multi-Class Classification: Softmax Activation
  • $y_{t}$에 softmax layer를 거는 형태로 output vector를 확률 분포 vector로 변환

 

 

• Regression Task: Linear Activation
  • $y_{t}$ 자체의 실수 값을 최종 예측 output으로 사용하게 되는 다양한 형태를 띄게 됨

 

 

 

취향에 따라 왼쪽 구조 혹은 오른쪽 구조로 표현하면 된다. (필자는 오른쪽 구조를 더 선호한다)

 

 

 

 

---

2. Various Problem Settings of RNN-based Sequence Modeling

 

 

 

Vanilla Neural Networks (one to one)

 

• time step의 개념없이 한번에 하나의 data item을 입력으로 받아서 해당 예측 결과를 반환
• time step $t = 1$일 때만 입력이 주어지고 그때 바로 해당하는 출력 결과물이 각각 나오게 되는 경우

 

 

 

one to many

 

• 최초 time step에 딱 한번 입력이 주어짐
• 다음 time step의 입력으로는 zero vector나 0으로 채워진 matrix or tensor가 입력으로 주어진다고도 생각 가능
• 출력 결과물은 여러 time step에 걸쳐서 순차적인 예측 결과를 생성 (입력이 하나고, 출력이 여러 개로 이루어진 sequence data)
• Ex) Image Captioning Task: RNN Module은 출력 결과물로서 이미지를 설명하는 텍스트의 각각의 단어들을 특정 sequence로 예측해주는 형태 

 

 

 

 

 

 

 

Many to One

 

• 입력이 sequence 형태로 주어지되, 최종적인 마지막 time step에서 단일한 time step의 예측결과를 생성
• Ex) 문장 분류 (Sentiment Classification)

 

 

문장 전체를 잘 읽은 후 문장 전체의 정보를 종합하여 last time step의 hidden state vector를 output layer에 input으로 제공하여 최종판단을 수행

 

 

 

Many to Many (Sequence-to-sequence)

 

• 일반화된 형태 (Seq2Seq Model의 기본적인 문제 setting)
• 입력, 출력 모두 sequence 형태로 주어짐: 입력 sequence를 다 읽은 후에 예측 sequence를 생성
• Ex) Machine Translation: 번역기

 

 

 

• 특수한 형태
  •  입력이 sequence로 주어졌을 때 예측 결과물을 실시간으로 그때까지 주어졌던 sequence를 바탕으로 매 time step마다 바로바로 예측 결과를 생성
  • delay를 허용하지 않음
  • Ex) Video Classification on Frame Level

 

 

 

 

 

---

3. Character-level Language Model

 

 

 

• Basic NLP Task: Language Modeling Task 중 하나
• 각 character level에서 input을 매 time step마다 받았을 때 다음에 나타날 character를 예측
• Delay를 허용하지 않음

5개의 character로 이루어진 하나의 training data가 주어짐

 

 

 

각각의 character를 하나의 vocabulary로 구성하고 vocabulary상에서 각각의 워드를 categorical variable 형태로 encoding 한다.

 

 

• Vocabulary: [h, e, l, o]
• Vocabulary상에서 각각의 word를 one-hot vector 형태로 나타냄

 

one-hot encoding된 input vector $x_{t}$를 받고, 전 time step에서 넘어오는 $h_{t-1}$를 이용하여 현재 hidden state vector $h_{t}$를 계산

 

 

 

 

$h_{t} = tanh(W_{xh}x_{t} + W_{hh}h_{t-1} + b)$

 

• $x_{t}$: 4차원 vector
• $W_{xh}$: $3 \times 4$ Matrix
• $h_{t-1}, h_{t}, b$: 3차원 vector
• $W_{hh}$: $3 \times 3$ Matrix 

 

 

 

이때, 최초의 time step에는 $h_{t-1}$이 존재하지 않기 때문에 Zero Vector를 입력으로 준다

 

 

 

각 time step 기준으로 그 다음에 나타내아 할 character를 예측해야 한다

 

 

 

 

prediction을 위해 output layer $y_{t}$를 이용한다

 

 

 

매 time step마다 4개의 class 중에 하나의 class를 예측하는 Multi-Class Clasification을 수행하고,

 

 

 

Output Vector $y_{t}$를 4차원 vector로 만든 후 softmax layer를 통과시키면 h, e, l, o의 4개의 class에 대응하는 probability vector를 얻게된다

 

 

 

이렇게 최종 예측값은 가장 큰 확률값을 부여하게 된 해당 class 를 다음에 나타날 character로 예측하게 된다

 

 

 

이후 ground truth class or character를 기준으로 해서 Cross-Entropy Loss를 최소화하며 network 전체를 학습하게 된다

 

 

 

해당 과정에서 Trainable Parameter인 $W_{xh}, W_{hh}, W_{hy}$가 Update 된다

 

 

 

Softmax Layer: 예측하고자 하는 대상인 4개의 character 중에 하나로 classification 해주는 probability vector를 반환

 

 

 

 

 

 

Trainable한 parameter: $W_{hy}, W_{hh}, W_{xh}$ 모두 Gradient Descent를 이용하여 학습이 진행됨

 

 

 

Model Train

 

• Ground Truth class info: 실제 'h' 뒤에 순서가 'ello'라는 정보
• Supervised Learning 방식으로 각 time step에서의 CE Loss를 구함 (Model Prediction vs Ground Truth Class)
• 해당 softmax 확률값에 log를 취하고 -를 붙여 Cross-Entorpy loss 값을 최소화하는 방식으로 학습을 진행

 

 

 

Model Test

 

• Softmax Activation에서 가장 큰 확률을 부여받은 Character를 해당 time step에서 다음에 나타날 character로 예측
• 그 예측된 character를 다음 time step에서 실제로 나타난 character라고 생각해서 다음 time step에 RNN에 input vector로 주게 된다
• 즉, 연쇄적으로 최초의 time step에서 character 하나만 입력으로 준다면 character의 예측된 sequence를 무한정 길이만큼 생성할 수 있음 

 

 

 

 

 

 

 

Layer의 구조를 다음과 같이 생각하자

 

• Input Layer
• Hidden Layer
• Output Layer
• Softmax

 

 

 

 

 

Auto Regressive Model

 

• Sequence Model에서 이전 time step에 예측한 결과가 다음 time step에 입력으로 주어지는 경우 
• Model의 output이 다음 time step의 input으로 주어지는 경우

 

 

 

 

 

 

 

 

 

 

 

• 학습을 진행할수록 유의미한 character sequence를 반환

 

 

• 논문 Paper이나 C code와 같은 코드도 만들어준다

 

 

 

 

---

4. Vanilla RNN 구조의 문제점

 

 

 

 

HELL -> ELLO 를 예측해주는 Vanilla (Plain) RNN 구조를 생각해보자

 

 

 

 

다음에 어떤 알파벳이 나와야 할까? (one-hot encoded)

 

 

 

'H, E, L, O' 의 4가지 중 하나의 알파벳이 나와야 하므로 Multi-class Classification이고, 

 

 

 

$\hat{y}$를 softmax activation에 적용시켜 Cross-Entropy Loss를 계산한다

 

 

 

즉, 각 time step의 4개 알파벳에 대해 Cross-Entropy Loss를 더해주면 된다

 

 

 

 

이때, 마지막 output vector가 'O'로 라벨링 되기 위해 최초의 time step에서의 input vector H가 Gradient에 미치는 영향력은?

 

 

 

 

 

편의상 알파벳이 3개라 하고, 모든 변수는 Scalar value로 가정한다

 

 

 

 

 

 

 

Activation Function의 gradient가 다른 time step의 Input vector에 비해 많이 곱해지기 때문에 gradient vanishing 문제가 발생한다

 

 

 

RNN의 구조적 한계

 

 

• Back propagation: 멀수록 잊혀진다
  • Activation Function의 Gradient가 점차 많이 곱해지기 때문에 gradient vanishing 문제가 발생한다

 

 

 

• Feed Forward (Forward propagation): 갈수록 흐려진다
  • Input Vector가 Activation Function을 많이 통과할 수록 기존에 가진 고유한 값이 점차 잊혀진다

 

 

 

즉, 학습이 불안정해지기 때문에 Plain RNN 구조를 실질적으로 많이 사용하지는 않는다

 

 

 

Problem

• Gradient Vainishing Problem
• Gradient Exploding Problem (gradient가 폭발적으로 늘어나게 되는 문제)

 

 

 

Solution

• RNN의 기본적인 입출력 setting은 동일하게 유지하되, 특정한 구조의 RNN 모델을 많이 사용
• LSTM(long-short term memory) or GRU(gated recurrent unit)를 사용

 

 

 

LSTM

 

• 기본적인 RNN의 i/o setting은 동일하게 유지
• RNN에서의 hidden state vector는 기존의 hidden state vector와 cell state vector로 두 가지 버젼의 vector들을 통해 입력 신호를 잘 처리하고 그 정보를 encoding한다

 

 

 

 

 

 

 

---

5. Code - Vanilla RNN

 

 

 

import torch
from torch import nn, optim
import matplotlib.pyplot as plt

 

BATCH_SIZE = 1
LR = 5e-1
EPOCH = 100
criterion = nn.CrossEntropyLoss()

 

 

torch.eye(4).tolist()

[[1.0, 0.0, 0.0, 0.0],
 [0.0, 1.0, 0.0, 0.0],
 [0.0, 0.0, 1.0, 0.0],
 [0.0, 0.0, 0.0, 1.0]]

 

 

num_classes = 4
input_size = 4
output_size = 4
hidden_size = 3

idx2char = ["h", "e", "l", "o"]
x_data = [0, 1, 2, 2]  # h, e, l, l
one_hot_lookup = torch.eye(4).tolist()
y_data = [1, 2, 2, 3]  # e, l, l, o
seq_len = 4

x_one_hot = [one_hot_lookup[x] for x in x_data]
X = torch.tensor(x_one_hot).unsqueeze(
    dim=0
)  # X.shape = (Data_size, seq_len, input_size)
Y = torch.tensor(y_data).reshape(1, -1, 1)  # Y.shape = (Data_size, seq_len, 1)

 

 

print(X)
print(Y)

tensor([[[1., 0., 0., 0.],
         [0., 1., 0., 0.],
         [0., 0., 1., 0.],
         [0., 0., 1., 0.]]])
tensor([[[1],
         [2],
         [2],
         [3]]])

 

 

class Custom_Dataset(torch.utils.data.Dataset):
    def __init__(self, X, Y, transform=None):
        self.X = X
        self.Y = Y
        self.transform = transform

    def __len__(self):
        return self.X.shape[0]

    def __getitem__(self, idx):
        x = self.X[idx]
        if self.transform:
            x = self.transform(x)
        y = self.Y[idx]
        return x, y


custom_DS = Custom_Dataset(X, Y)
train_DL = torch.utils.data.DataLoader(custom_DS, batch_size=BATCH_SIZE, shuffle=False)

 

 

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super().__init__()
        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            batch_first=True,
            nonlinearity="tanh",
        )
        self.fc = nn.Linear(hidden_size, output_size)

    def forward(self, x, h_init):
        # out, h = self.rnn(x, h_init) # x.shape = (BS,seq_len,input_size)
        # out.shape = (BS,seq_len,hidden_size), h.shape = (D*num_layer, BS, hidden_size)

        # rnn cell 한번씩 통과시켜서 각 hi 를 저장하자
        self.h = []
        out = torch.tensor([])
        hi = h_init
        for j in range(seq_len):
            x_letter = x[:, j, :].unsqueeze(
                dim=1
            )  # x.shape = (BS,seq_len,input_size) 를 맞춰줌
            _, hi = self.rnn(x_letter, hi)  # y_hat.shape = (BS,seq_len,hidden_size)
            hi.retain_grad()
            self.h += [hi]
            out = torch.cat(
                [out, hi.permute(1, 0, 2)], dim=1
            )  # out.shape = (BS,seq_len,hidden_size)
            # .permite(1,0,2) 는 사실 D*num_layer=1 이라서 가능한거지 엄밀하게는 틀림
        out = self.fc(out)  # x.shape = (BS,seq_len,output_size)
        return out

 

 

model = RNN(input_size, hidden_size, output_size)
print(model)
x_batch, _ = next(iter(train_DL))  # x.shape = (BS,seq_len,input_size) 를 맞춰줌
h_init = torch.zeros(
    1, x_batch.shape[0], hidden_size
)  # h.shape = (D*num_layer, BS, hidden_size) 를 맞춰줌
y_hat = model(x_batch, h_init)  # 0 번째 글자

RNN(
  (rnn): RNN(4, 3, batch_first=True)
  (fc): Linear(in_features=3, out_features=4, bias=True)
)

 

 

def Train(model, train_DL, criterion, **kwargs):
    optimizer = optim.SGD(model.parameters(), lr=kwargs["LR"])

    NoT = len(train_DL.dataset)  # Number of training data
    loss_history = []
    mean_grad_history = torch.tensor([])

    model.train()  # train mode로!
    h_init = torch.zeros(
        1, BATCH_SIZE, hidden_size
    )  # h.shape = (D*num_layer, BS, hidden_size) 를 맞춰줌
    for ep in range(kwargs["EPOCH"]):
        rloss = 0
        rgrad = torch.zeros(seq_len)
        print("predicted string: ", end="")
        for x_batch, y_batch in train_DL:
            # x_batch.shape = (BS, seq_len, input_size)
            # y_batch.shape = (BS, seq_len, 1)
            # grad (batch)
            h_init = torch.zeros(1, x_batch.shape[0], hidden_size)
            y_hat = model(x_batch, h_init)  # y_hat.shape = (BS,seq_len,hidden_size)
            L4 = criterion(
                y_hat[0, -1, :].reshape(1, -1), y_batch[0, -1, :].reshape(-1)
            )  # y_batch는 1D 여야 함
            # 0 번째 data에 대해서만 L4 계산 (멀수록 잊혀지는 현상만 보기 위해)
            L4.backward()
            rgrad += torch.tensor(
                [model.h[i].grad.abs().sum() * x_batch.shape[0] for i in range(seq_len)]
            )
            # inference
            y_hat = model(x_batch, h_init)
            # cross entropy loss
            loss = 0
            for i in range(x_batch.shape[0]):
                loss += criterion(
                    y_hat[i], y_batch[i].reshape(-1)
                )  # y_batch는 1D 여야 함
                pred = y_hat[i].argmax(dim=1)
                print(*[idx2char[p] for p in pred], sep="")
            # update
            optimizer.zero_grad()  # gradient 누적을 막기 위함
            loss.backward()  # backpropagation
            optimizer.step()  # weight update
            # loss accumulation
            loss_b = (
                loss.item() * x_batch.shape[0]
            )  # batch loss # BATCH_SIZE 로 하면 마지막 16개도 32개로 계산해버림
            rloss += loss_b  # running loss
        # grad and weight (epoch)
        mean_grad_history = torch.cat(
            [mean_grad_history, rgrad.reshape(1, -1) / NoT], dim=0
        )
        # print loss
        loss_e = rloss / NoT  # epoch loss
        loss_history += [loss_e]
        print("Epoch:", ep + 1, "train loss:", round(loss_e, 5))
        print("-" * 20)
    return loss_history, mean_grad_history

 

 

model = RNN(input_size, hidden_size, output_size)
loss_history, mean_grad_history = Train(model, train_DL, criterion, LR=LR, EPOCH=EPOCH)

predicted string: oeoo
Epoch: 1 train loss: 1.57371
--------------------
predicted string: leoo
Epoch: 2 train loss: 1.37276
--------------------
predicted string: llll
Epoch: 3 train loss: 1.25721
--------------------
predicted string: llll
Epoch: 4 train loss: 1.18172
--------------------
predicted string: llll
Epoch: 5 train loss: 1.12777
--------------------
predicted string: llll
Epoch: 6 train loss: 1.08475
--------------------
predicted string: llll
Epoch: 7 train loss: 1.04629
--------------------
predicted string: llll
Epoch: 8 train loss: 1.00853
--------------------
predicted string: llll
Epoch: 9 train loss: 0.96872
--------------------
predicted string: llll
Epoch: 10 train loss: 0.92462
--------------------
predicted string: llll
Epoch: 11 train loss: 0.8745
--------------------
predicted string: llll
Epoch: 12 train loss: 0.81776
--------------------
predicted string: lllo
Epoch: 13 train loss: 0.75557
--------------------
predicted string: ello
Epoch: 14 train loss: 0.69065
--------------------
predicted string: ello
Epoch: 15 train loss: 0.62608
--------------------
predicted string: ello
Epoch: 16 train loss: 0.56454
--------------------
predicted string: ello
Epoch: 17 train loss: 0.50779
--------------------
predicted string: ello
Epoch: 18 train loss: 0.45663
--------------------
predicted string: ello
Epoch: 19 train loss: 0.41113
--------------------
predicted string: ello
Epoch: 20 train loss: 0.37096
--------------------
predicted string: ello
Epoch: 21 train loss: 0.33563
--------------------
predicted string: ello
Epoch: 22 train loss: 0.30461
--------------------
predicted string: ello
Epoch: 23 train loss: 0.27739
--------------------
predicted string: ello
Epoch: 24 train loss: 0.25351
--------------------
predicted string: ello
Epoch: 25 train loss: 0.23254
--------------------
predicted string: ello
Epoch: 26 train loss: 0.21411
--------------------
predicted string: ello
Epoch: 27 train loss: 0.19788
--------------------
predicted string: ello
Epoch: 28 train loss: 0.18356
--------------------
predicted string: ello
Epoch: 29 train loss: 0.17087
--------------------
predicted string: ello
Epoch: 30 train loss: 0.1596
--------------------
predicted string: ello
Epoch: 31 train loss: 0.14955
--------------------
predicted string: ello
Epoch: 32 train loss: 0.14056
--------------------
predicted string: ello
Epoch: 33 train loss: 0.13249
--------------------
predicted string: ello
Epoch: 34 train loss: 0.12521
--------------------
predicted string: ello
Epoch: 35 train loss: 0.11862
--------------------
predicted string: ello
Epoch: 36 train loss: 0.11264
--------------------
predicted string: ello
Epoch: 37 train loss: 0.10719
--------------------
predicted string: ello
Epoch: 38 train loss: 0.10222
--------------------
predicted string: ello
Epoch: 39 train loss: 0.09765
--------------------
predicted string: ello
Epoch: 40 train loss: 0.09346
--------------------
predicted string: ello
Epoch: 41 train loss: 0.08959
--------------------
predicted string: ello
Epoch: 42 train loss: 0.08601
--------------------
predicted string: ello
Epoch: 43 train loss: 0.08269
--------------------
predicted string: ello
Epoch: 44 train loss: 0.07961
--------------------
predicted string: ello
Epoch: 45 train loss: 0.07674
--------------------
predicted string: ello
Epoch: 46 train loss: 0.07406
--------------------
predicted string: ello
Epoch: 47 train loss: 0.07156
--------------------
predicted string: ello
Epoch: 48 train loss: 0.06921
--------------------
predicted string: ello
Epoch: 49 train loss: 0.06701
--------------------
predicted string: ello
Epoch: 50 train loss: 0.06494
--------------------
predicted string: ello
Epoch: 51 train loss: 0.06299
--------------------
predicted string: ello
Epoch: 52 train loss: 0.06115
--------------------
predicted string: ello
Epoch: 53 train loss: 0.05941
--------------------
predicted string: ello
Epoch: 54 train loss: 0.05776
--------------------
predicted string: ello
Epoch: 55 train loss: 0.05621
--------------------
predicted string: ello
Epoch: 56 train loss: 0.05473
--------------------
predicted string: ello
Epoch: 57 train loss: 0.05332
--------------------
predicted string: ello
Epoch: 58 train loss: 0.05198
--------------------
predicted string: ello
Epoch: 59 train loss: 0.05071
--------------------
predicted string: ello
Epoch: 60 train loss: 0.0495
--------------------
predicted string: ello
Epoch: 61 train loss: 0.04834
--------------------
predicted string: ello
Epoch: 62 train loss: 0.04724
--------------------
predicted string: ello
Epoch: 63 train loss: 0.04618
--------------------
predicted string: ello
Epoch: 64 train loss: 0.04517
--------------------
predicted string: ello
Epoch: 65 train loss: 0.0442
--------------------
predicted string: ello
Epoch: 66 train loss: 0.04327
--------------------
predicted string: ello
Epoch: 67 train loss: 0.04238
--------------------
predicted string: ello
Epoch: 68 train loss: 0.04152
--------------------
predicted string: ello
Epoch: 69 train loss: 0.0407
--------------------
predicted string: ello
Epoch: 70 train loss: 0.03991
--------------------
predicted string: ello
Epoch: 71 train loss: 0.03915
--------------------
predicted string: ello
Epoch: 72 train loss: 0.03841
--------------------
predicted string: ello
Epoch: 73 train loss: 0.03771
--------------------
predicted string: ello
Epoch: 74 train loss: 0.03703
--------------------
predicted string: ello
Epoch: 75 train loss: 0.03637
--------------------
predicted string: ello
Epoch: 76 train loss: 0.03573
--------------------
predicted string: ello
Epoch: 77 train loss: 0.03512
--------------------
predicted string: ello
Epoch: 78 train loss: 0.03453
--------------------
predicted string: ello
Epoch: 79 train loss: 0.03395
--------------------
predicted string: ello
Epoch: 80 train loss: 0.0334
--------------------
predicted string: ello
Epoch: 81 train loss: 0.03286
--------------------
predicted string: ello
Epoch: 82 train loss: 0.03234
--------------------
predicted string: ello
Epoch: 83 train loss: 0.03184
--------------------
predicted string: ello
Epoch: 84 train loss: 0.03135
--------------------
predicted string: ello
Epoch: 85 train loss: 0.03087
--------------------
predicted string: ello
Epoch: 86 train loss: 0.03041
--------------------
predicted string: ello
Epoch: 87 train loss: 0.02997
--------------------
predicted string: ello
Epoch: 88 train loss: 0.02953
--------------------
predicted string: ello
Epoch: 89 train loss: 0.02911
--------------------
predicted string: ello
Epoch: 90 train loss: 0.0287
--------------------
predicted string: ello
Epoch: 91 train loss: 0.0283
--------------------
predicted string: ello
Epoch: 92 train loss: 0.02791
--------------------
predicted string: ello
Epoch: 93 train loss: 0.02754
--------------------
predicted string: ello
Epoch: 94 train loss: 0.02717
--------------------
predicted string: ello
Epoch: 95 train loss: 0.02681
--------------------
predicted string: ello
Epoch: 96 train loss: 0.02646
--------------------
predicted string: ello
Epoch: 97 train loss: 0.02612
--------------------
predicted string: ello
Epoch: 98 train loss: 0.02579
--------------------
predicted string: ello
Epoch: 99 train loss: 0.02547
--------------------
predicted string: ello
Epoch: 100 train loss: 0.02515
--------------------

 

 

plt.figure(figsize=[15,8])
plt.plot(range(1,EPOCH+1), mean_grad_history[:,0], label = "$\Sigma$ |h1.grad|", linewidth=3)
plt.plot(range(1,EPOCH+1), mean_grad_history[:,1], label = "$\Sigma$ |h2.grad|", linewidth=3)
plt.plot(range(1,EPOCH+1), mean_grad_history[:,2], label = "$\Sigma$ |h3.grad|", linewidth=3)
plt.plot(range(1,EPOCH+1), mean_grad_history[:,3], label = "$\Sigma$ |h4.grad|", linewidth=3)
plt.xlabel("Epoch", fontsize=20)
plt.ylabel("mean absolute grad value", fontsize=20)
plt.legend(fontsize=20)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.grid()

 

$\frac{\partial L_{3}}{\partial W_{xh}}$는 summation 형태의 하나의 value 표현되어 있으므로 비교하기 힘들다

 

 

 

 

편법으로, 각 time step 에서의 $\frac{\partial L_{3}}{\partial h_{n}}$를 비교하자

 

 

 

실제로 Gradient의 크기를 비교하면 Activation Function의 Gradient가 더 많이 곱해진

 

 

초반 time step의 Hidden state vector에 대한 Gradient의 크기가

 

 

더 작을 수 밖에 없기에 각 Graph의 상하관계는 뒤집히지 않는다