1. Machine Learning & Deep Learning
AI (Artificial Intelligence)
- 지능형 기계를 만드는 과학이나 공학의 분야 / 인간의 지능(지적능력, 사고방식) 을 인공적으로 컴퓨터 시스템을 통해 구현한 것
ML (Machine Learning)
- 입력 데이터가 주어졌을 때 답을 유추해 줄 수 있는 최적의 함수를 기계가 찾는 것
- 기존 데이터에 알고리즘을 사용해 모델을 만들어내고, 새로운 데이터에 해당 모델을 적용시켜 패턴을 학습하고 결과를 추론하는 기법
- 데이터를 기반으로 통계적인 신뢰도를 강화
- 예측 오류를 최소화하기 위해 다양한 수학적 기법을 사용
- 데이터 내의 패턴을 스스로 인지하고 신뢰도있는 예측결과를 도출해 내는 함수를 찾는 것

- 머신러닝 개요
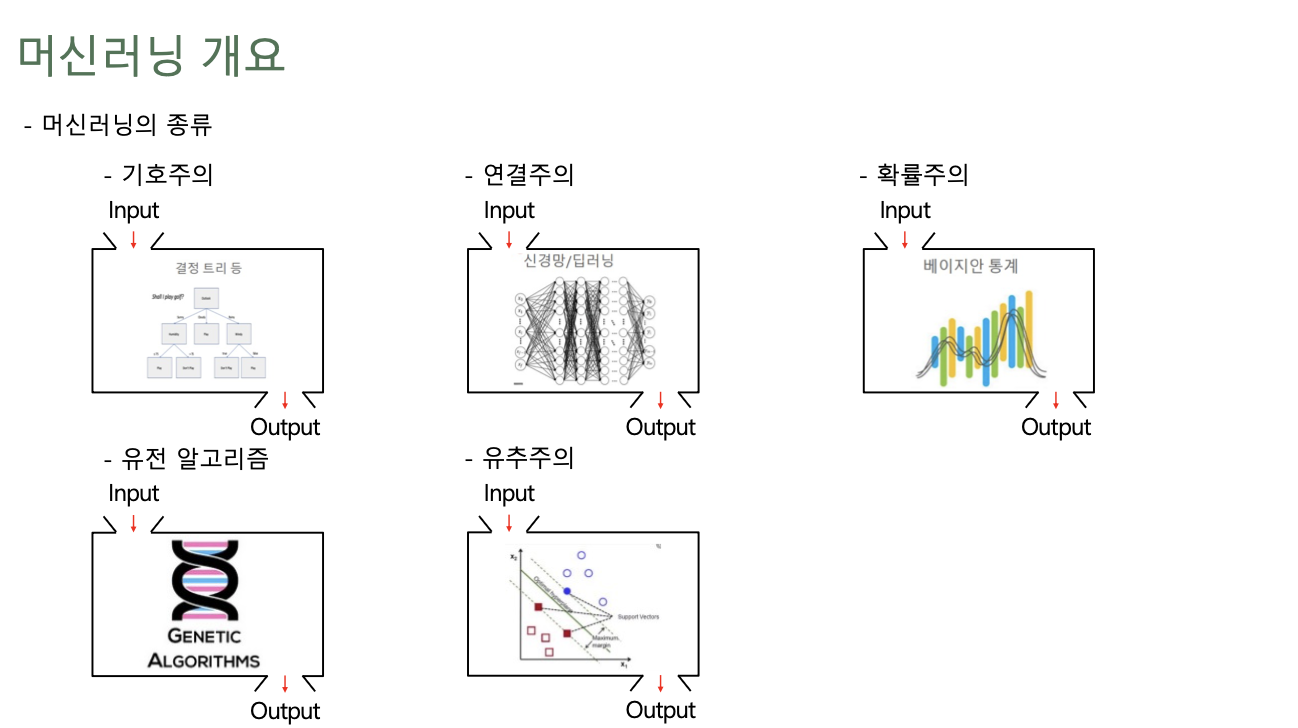
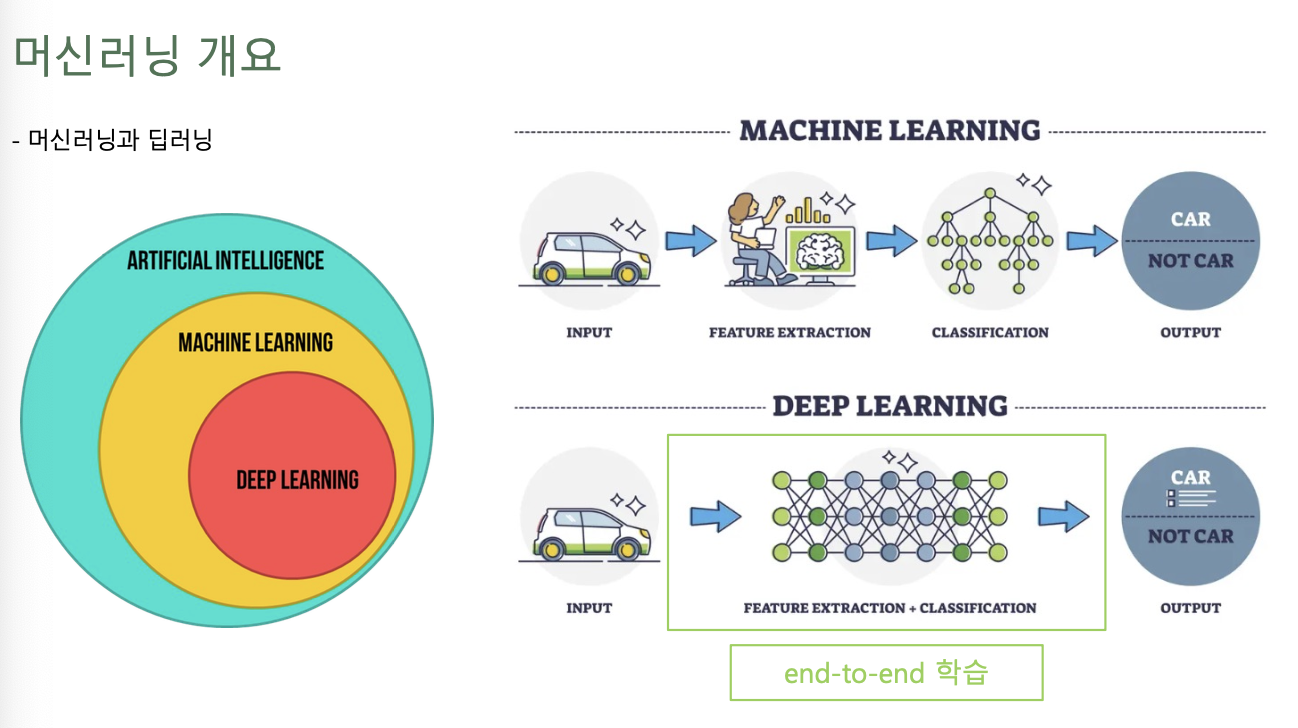
DL (Deep Learning)
- 머신러닝의 방법론 중 하나 (비선형 정보처리를 수행하는 계층을 여러 겹으로 쌓아서 학습모델을 구현하는 머신러닝의 한 분야)
- 엄청나게 많은 데이터에서 중요한 패턴을 잘 찾아냄, 규칙도 잘 찾아내고, 의사결정을 잘하게 됨
2. Perceptron
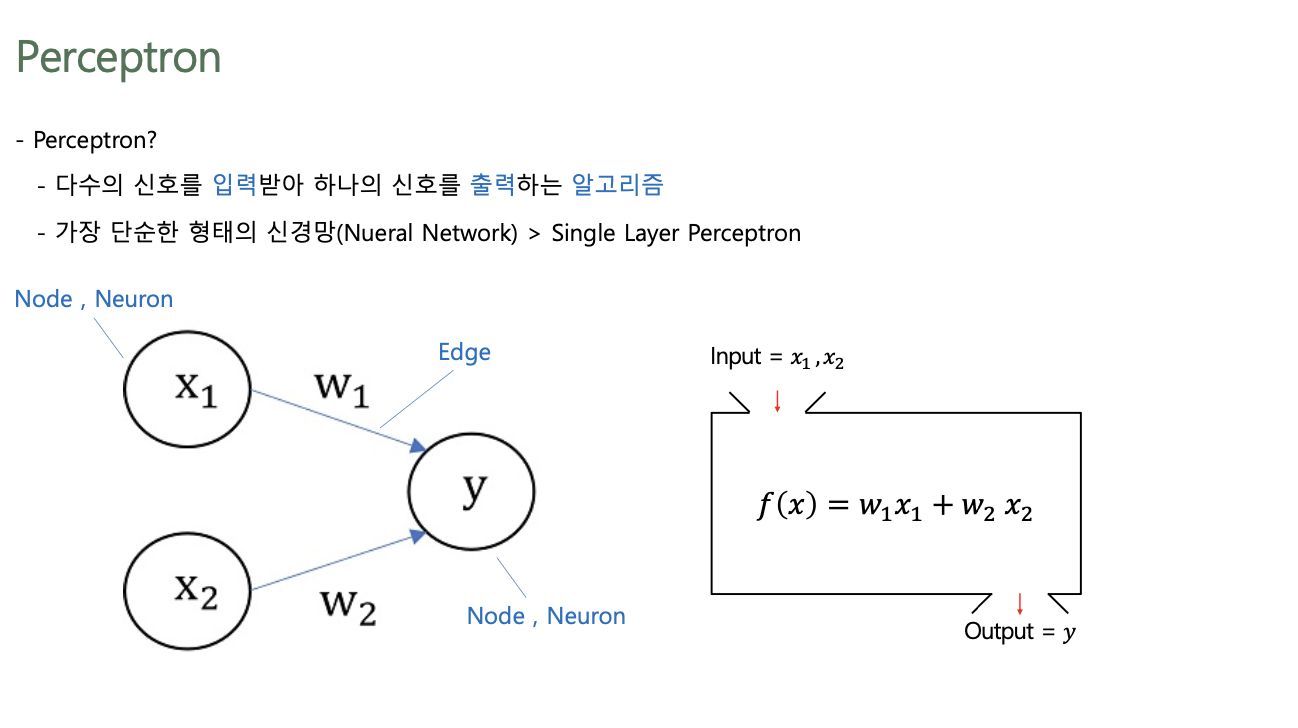
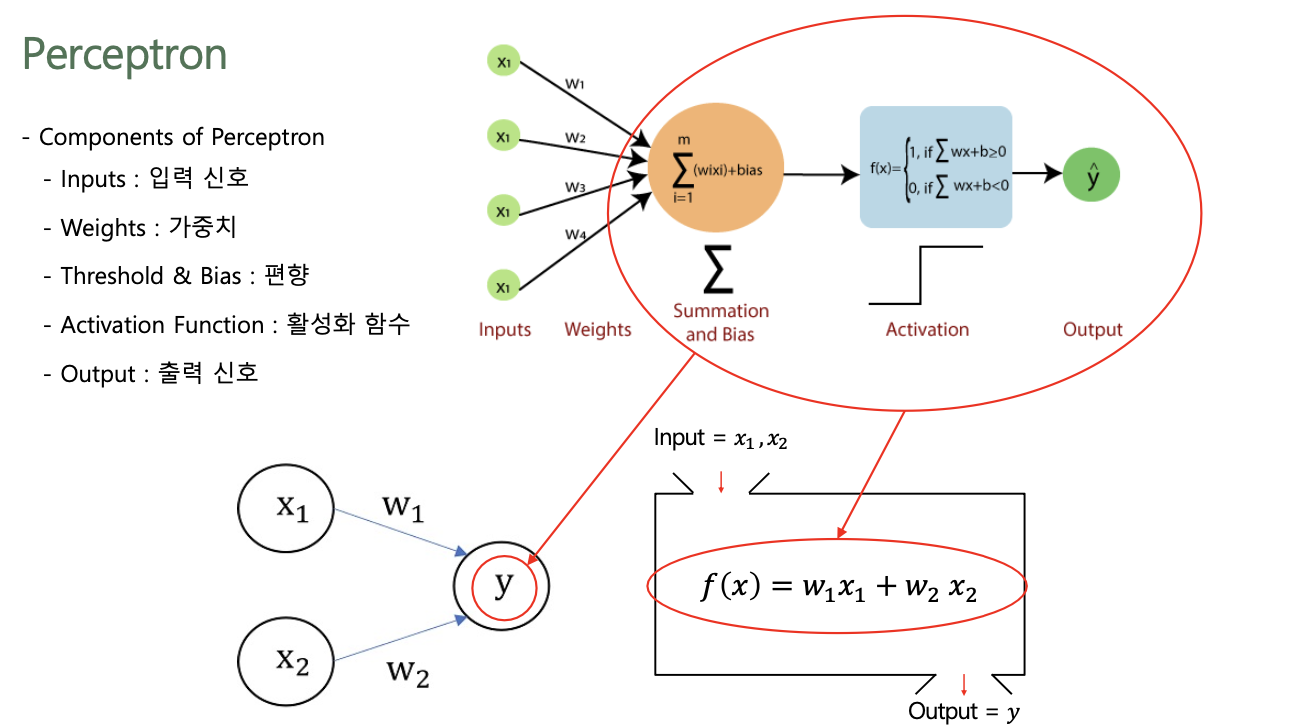
Perceptron
- 다수의 신호를 입력받아 하나의 신호를 출력하는 알고리즘
- 가장 단순한 형태의 신경망(Neural Network): Single Layer Perceptron
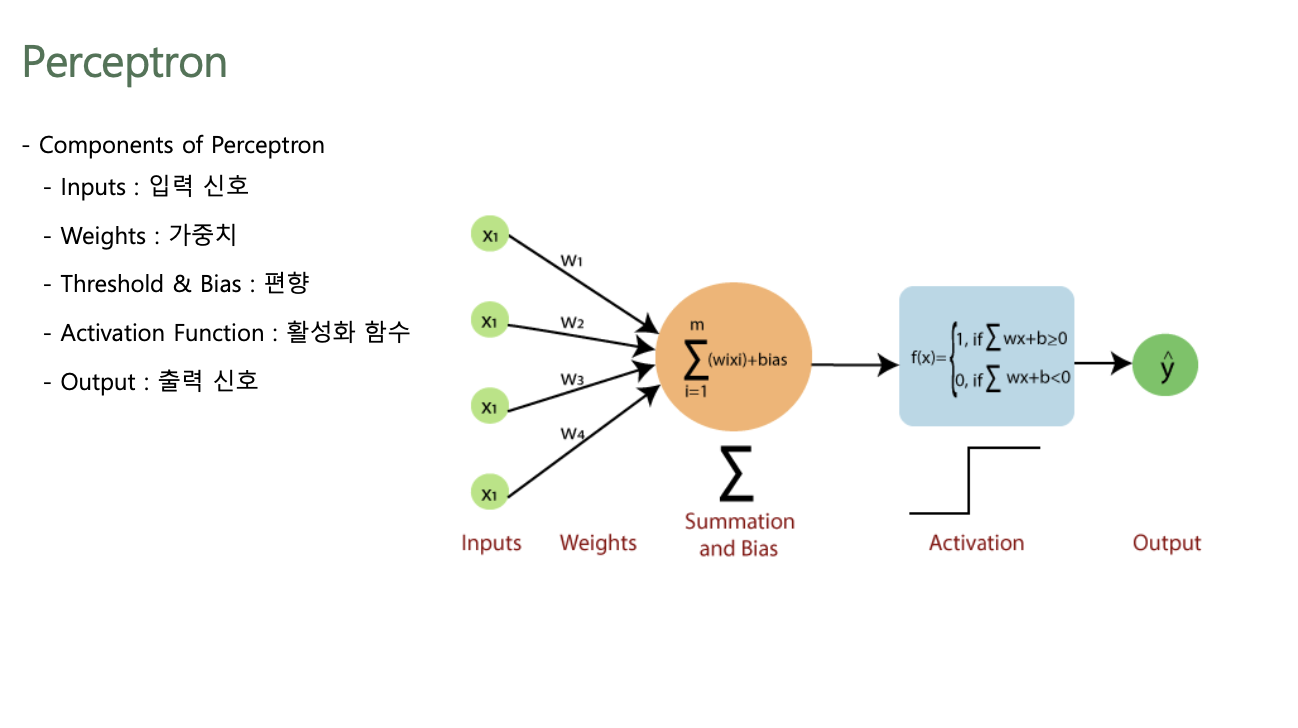
Components of Perceptron
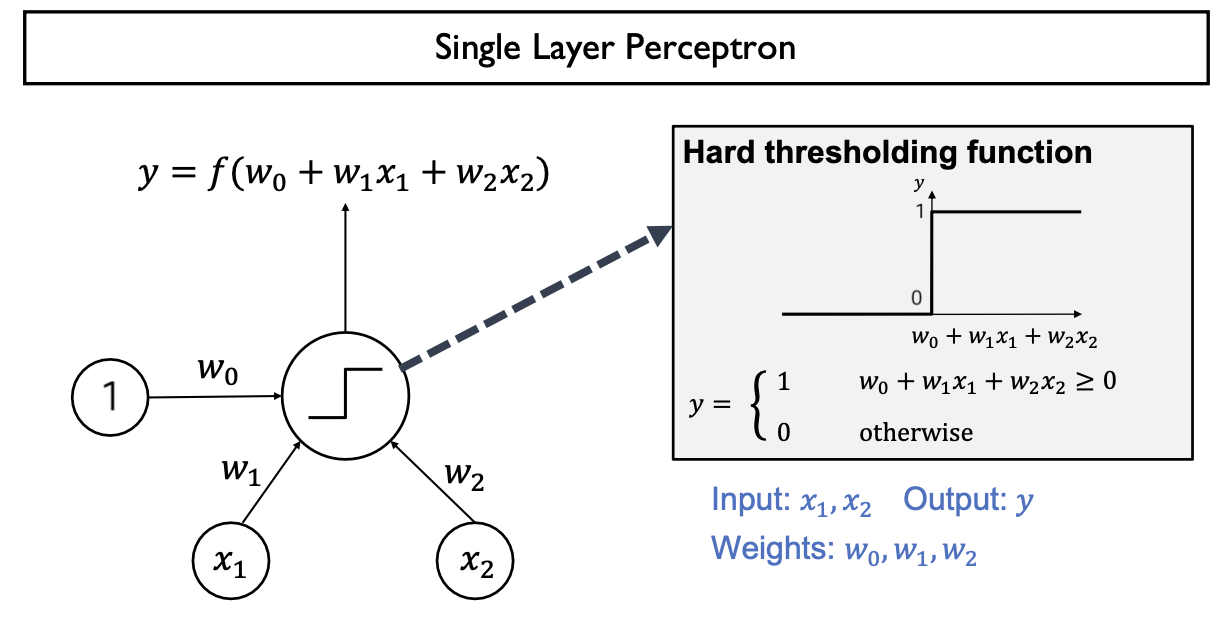
- Input Features(Input Vectors): $x_{1}, x_{2}$
- Model Parameters(Weight): $w_{0}, w_{1}, w_{2}$
- Linear Combination: $w_{0} + w_{1}x_{1} + w_{2}x_{2}$
- Activation Function: $f(x)$
- Output: $f(w_{0} + w_{1}x_{1} + w_{2}x_{2})$
Logic Gates w/ Perceptron
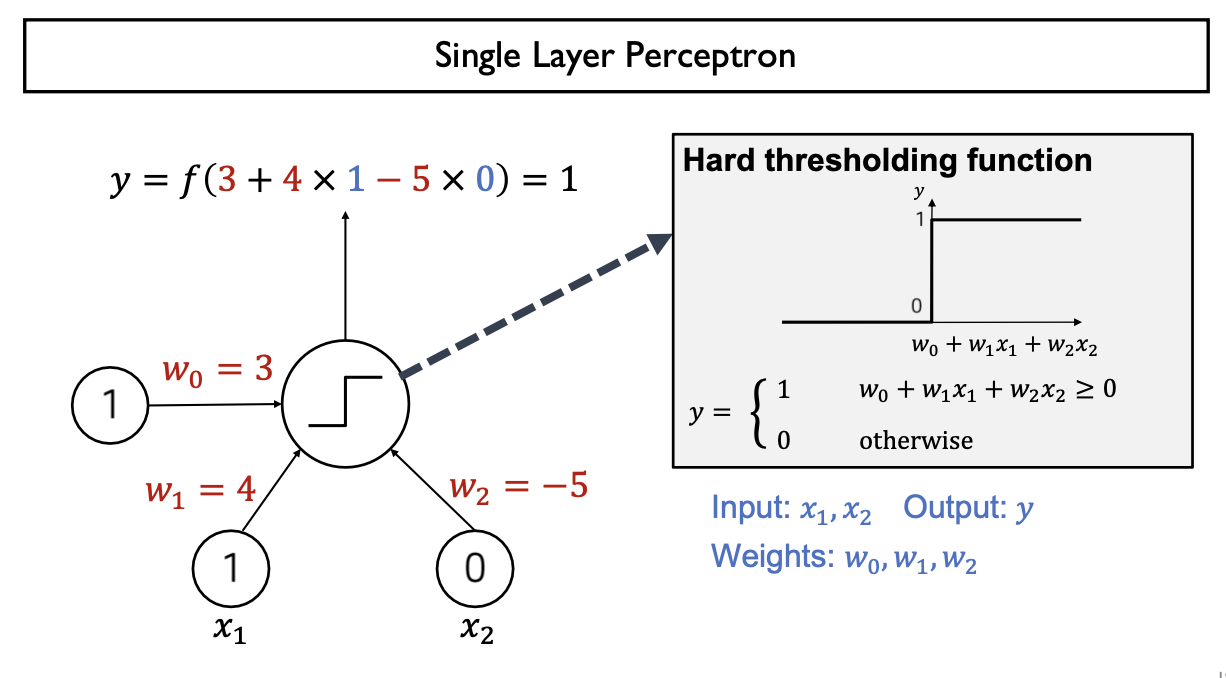
Single Layer Perceptron(w/ Hard thresholding function)은 Linear Problem (Linear Model)만 해결가능 (구현가능)
Non-Linear Problem (Non-Linear Model)을 어떻게 해결(구현) 하는가?
- 고차원 항을 추가: Kernel Perceptron (커널화된 퍼셉트론)을 사용
- 다계층을 활용 (XOR Problem)
Logic Gates
- AND: 둘 다 1이여야만 1 (곱한다고 생각)
- OR: 둘 중 하나만 1이면 1 (더한다고 생각, 1 OR 1 = 1에 주의)
- NAND: AND Gate출력에 NOT Gate 처리
- NOR: OR Gate 출력에 NOT Gate 처리
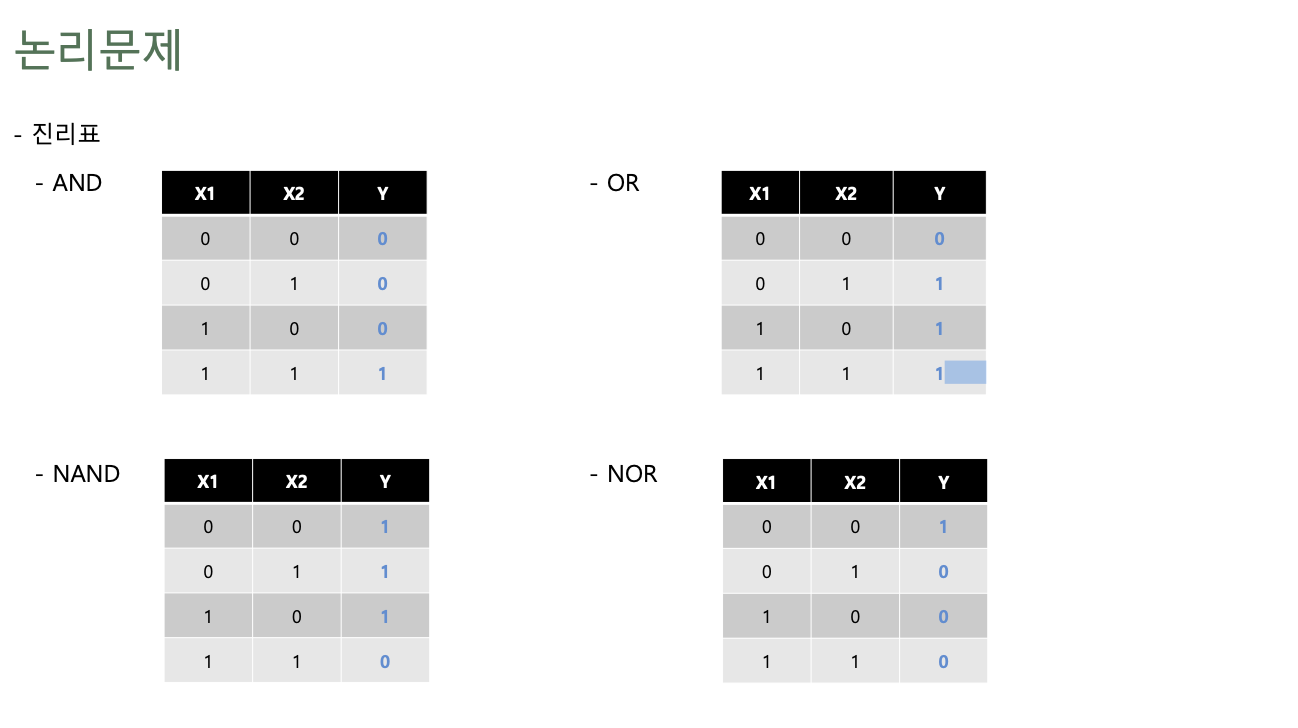
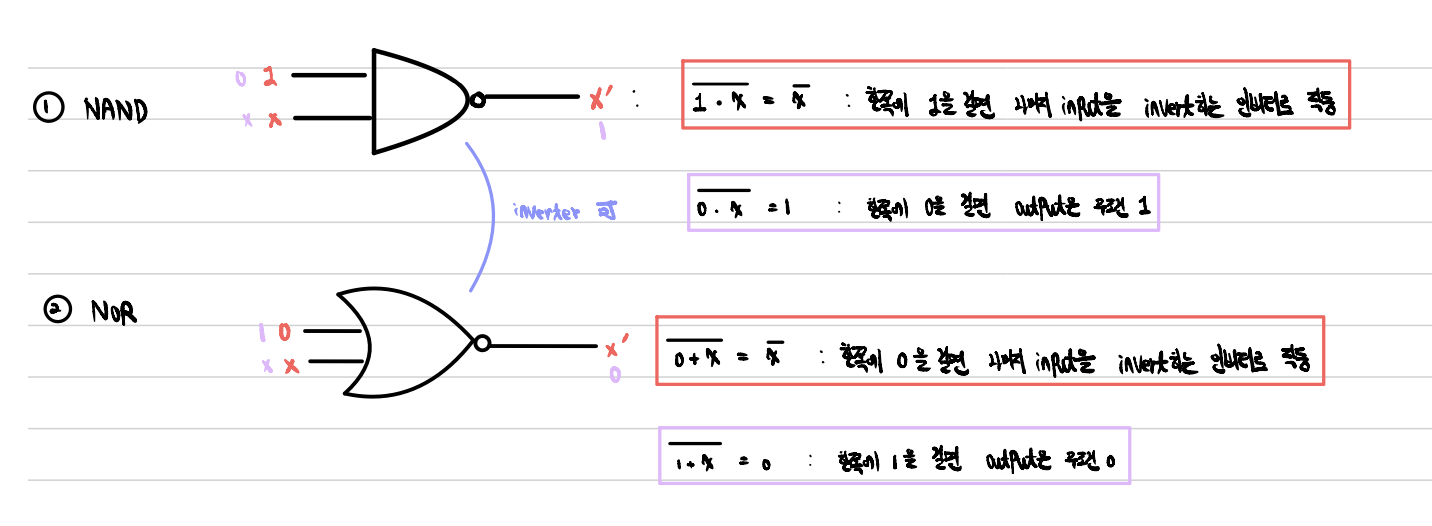
- NAND, NOR Gate 보충설명
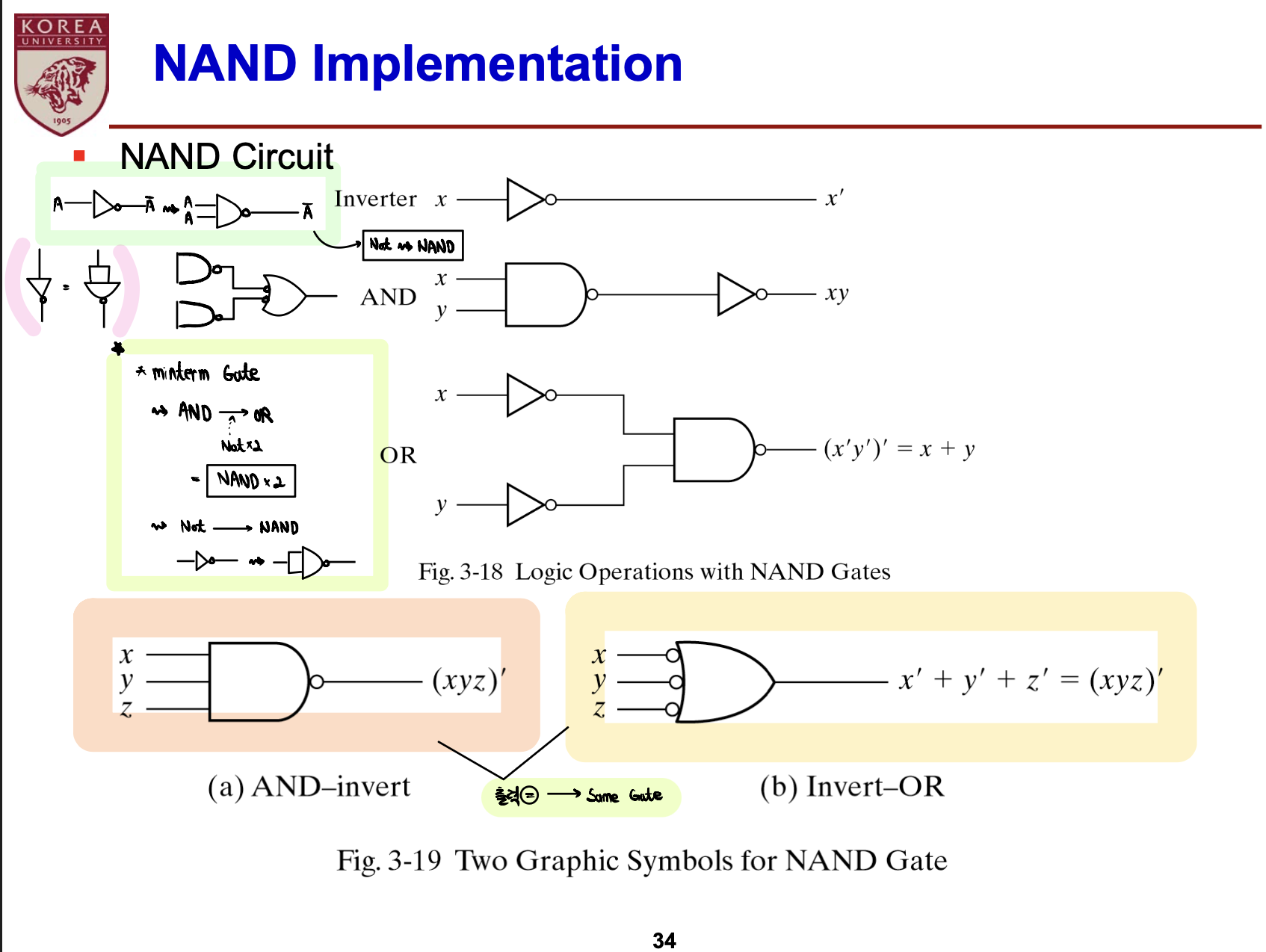
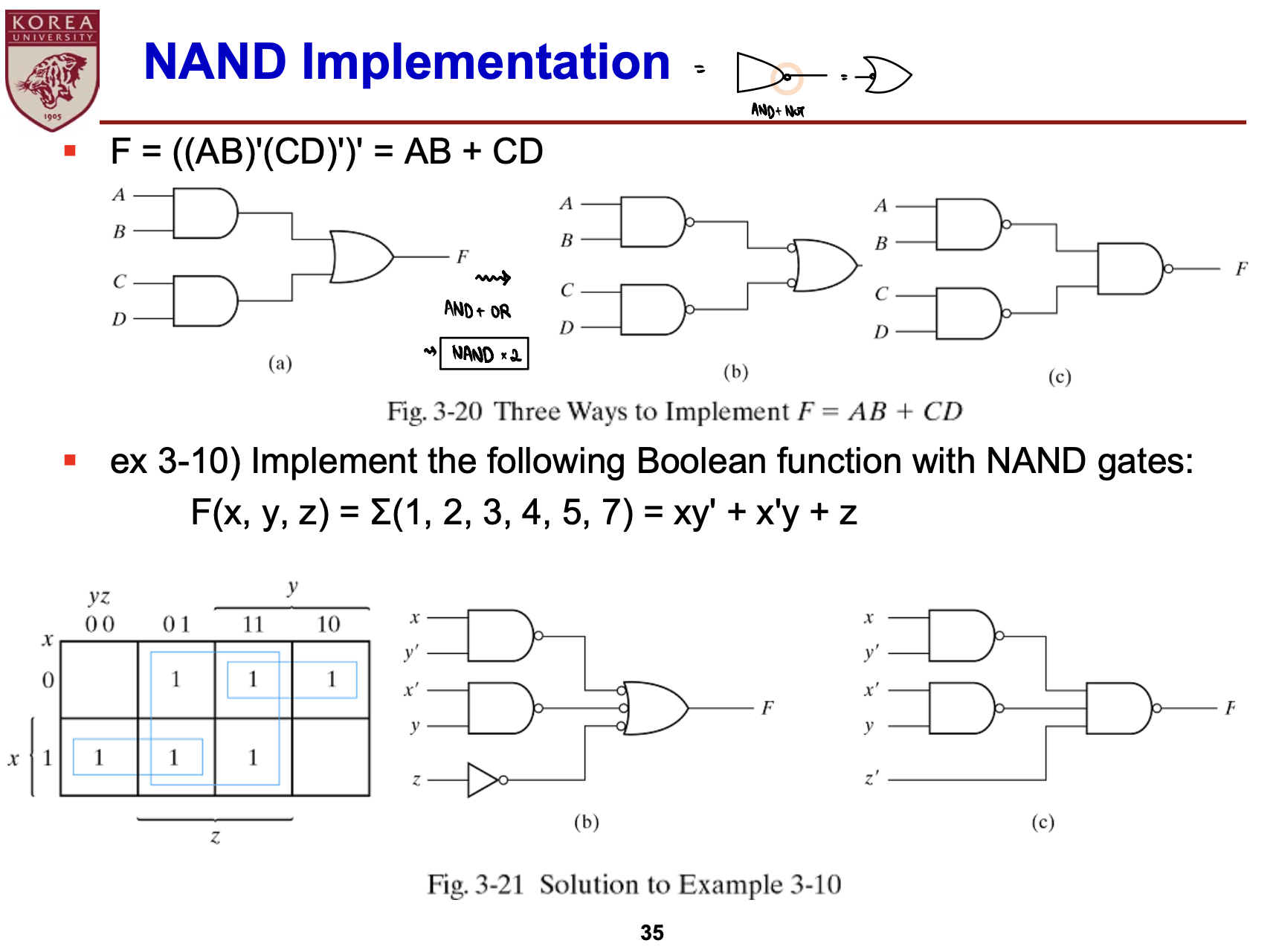
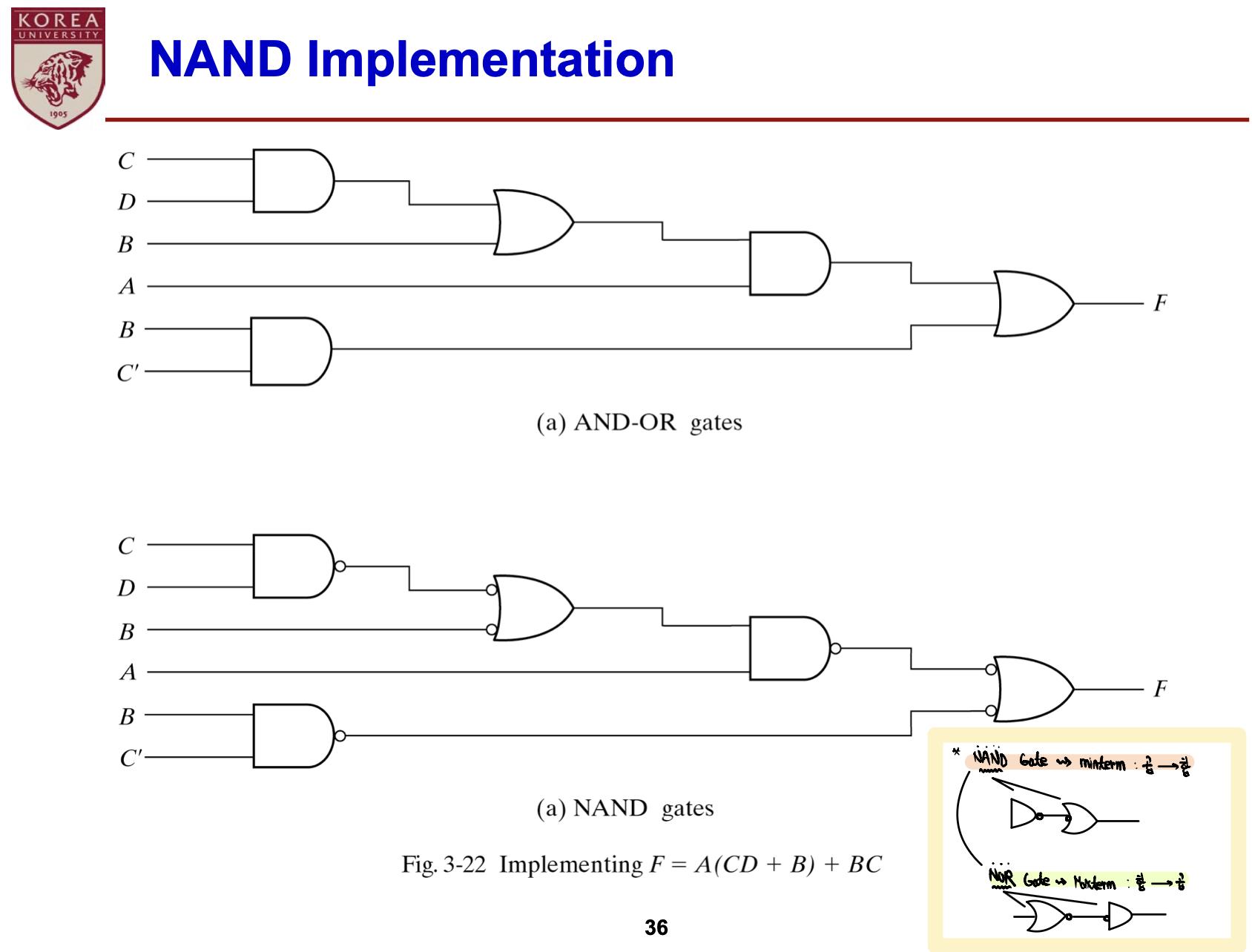
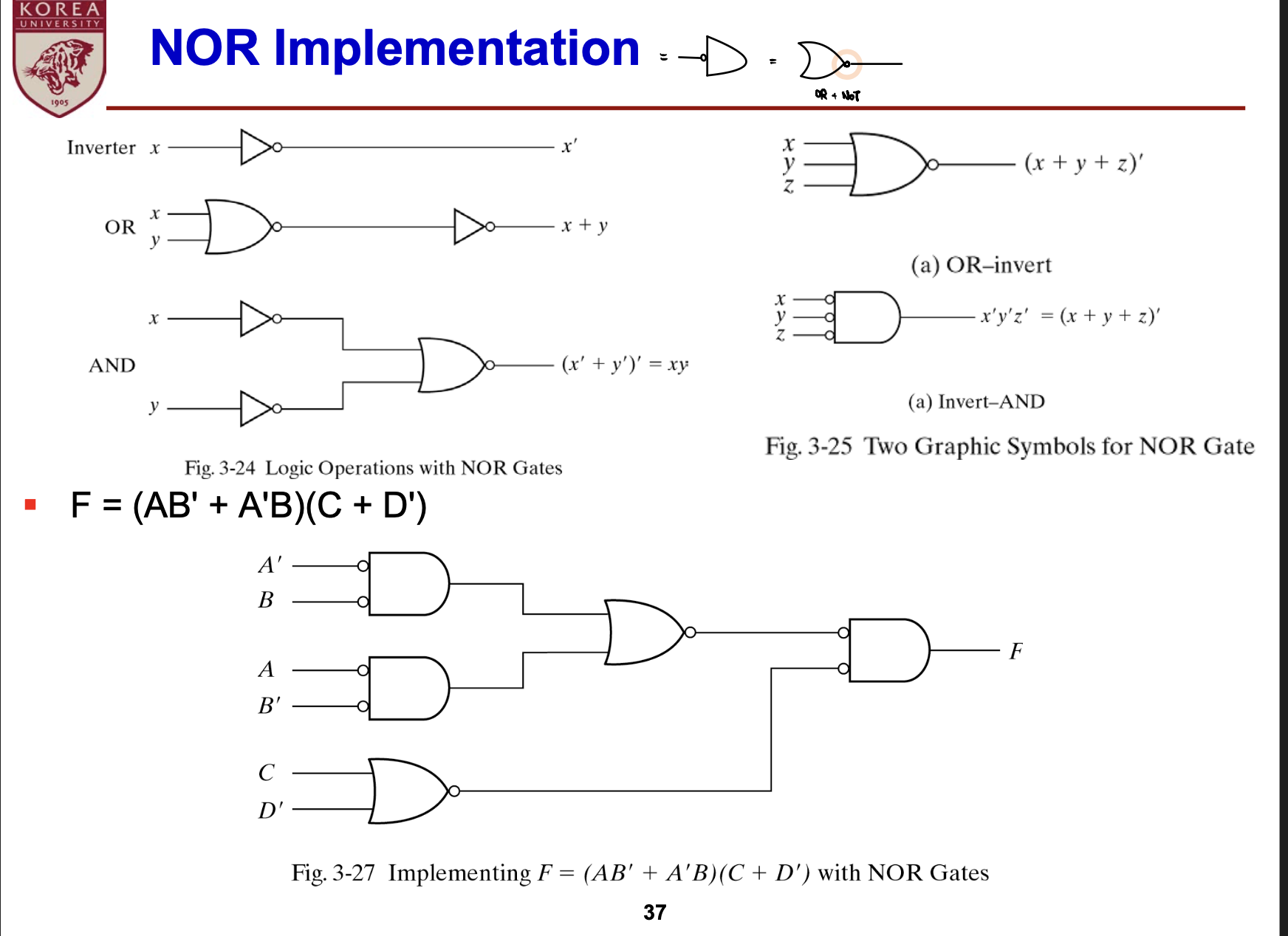
- NAND, NOR: Invertor로 작동하도록 설계 가능
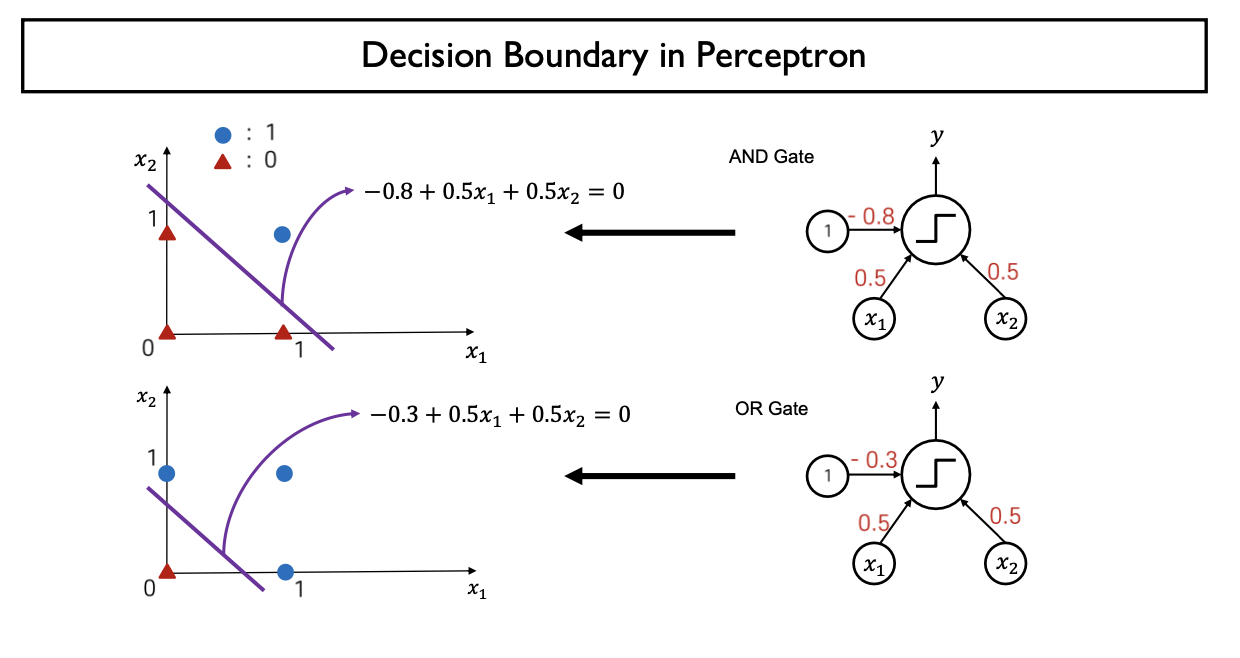
- Decision Boundary
- $Linear \: Combination(Score) =0$ 인 Hyper Plane
- $w_{0} + w_{1}x_{1} + w_{2}x_{2} = 0$
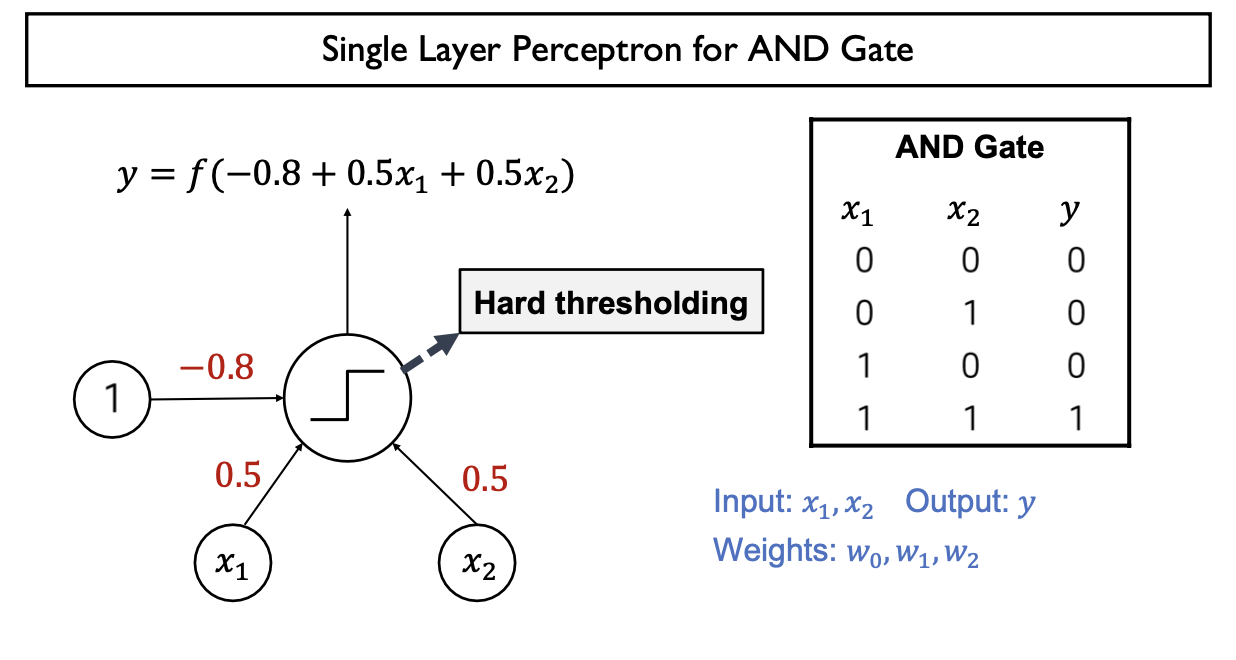
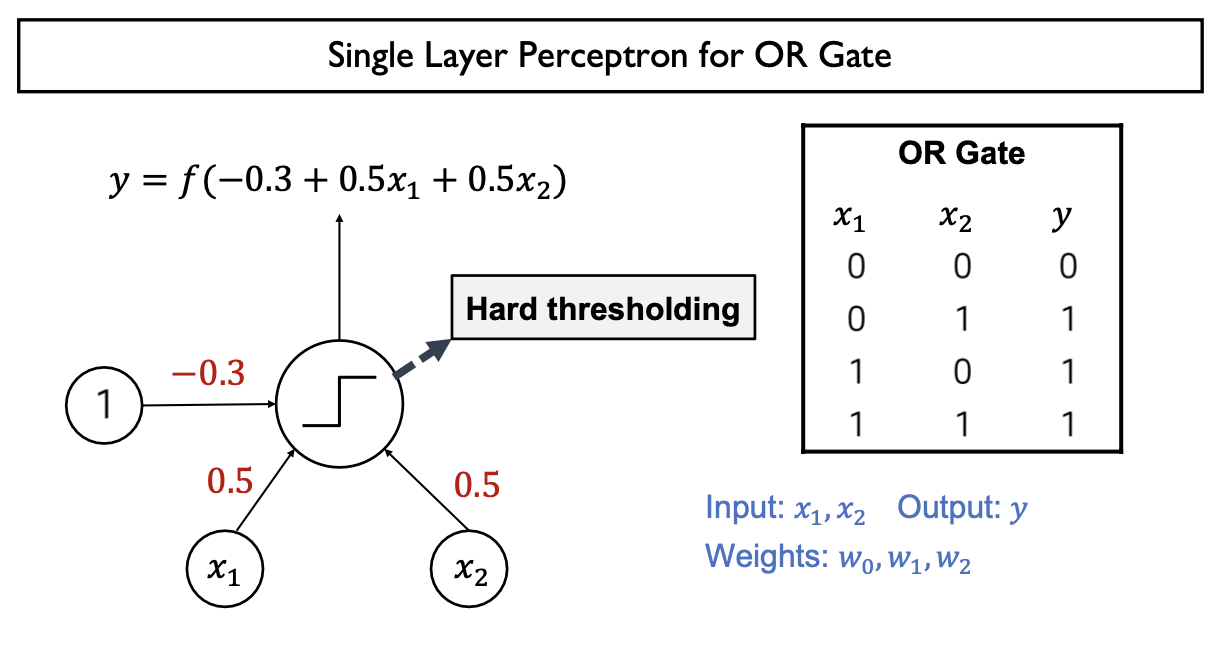
- AND, OR Gate 구현 (single layer perceptron)
- Model parameter (가중치 weight)을 적절하게 조정하여 AND, OR Gate 모두 설계가능
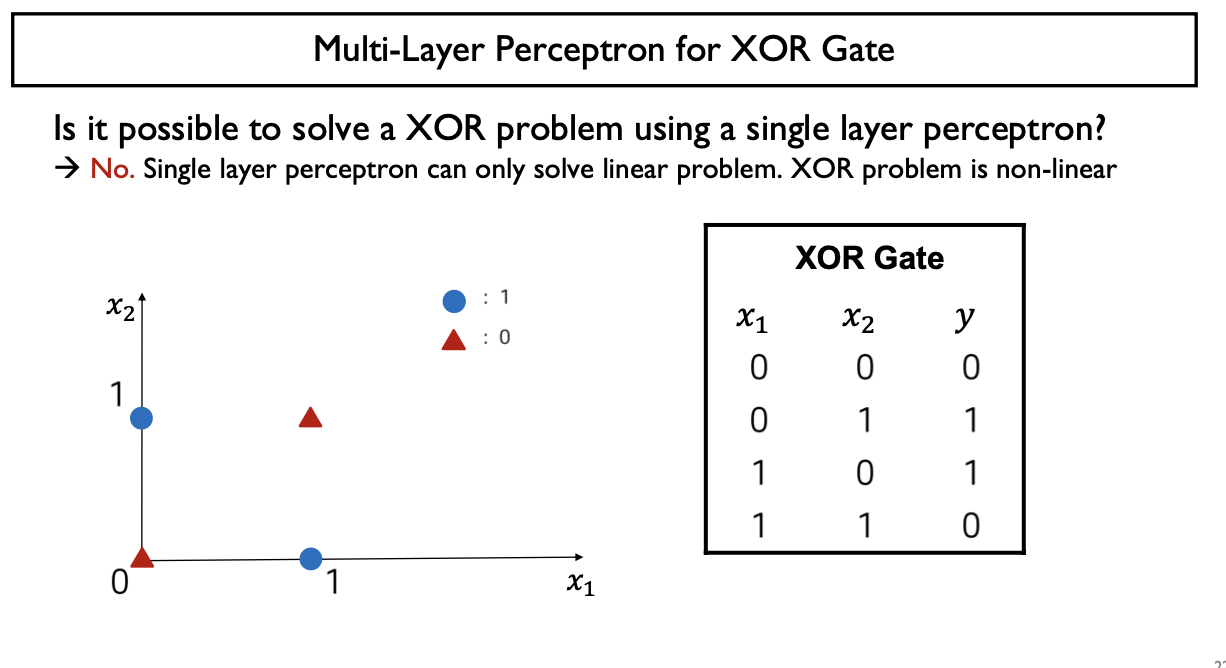
- Single layer perceptron은 only linear problem만 해결가능


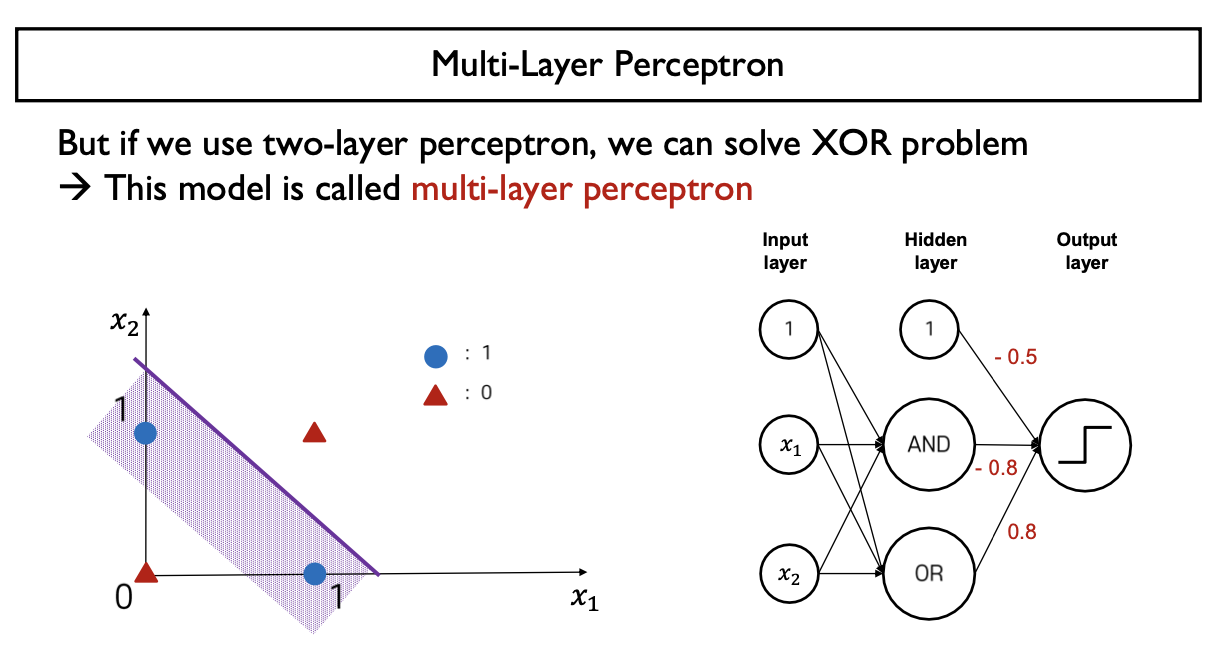
- XOR Gate 구현 (MLP 이용)
- Multi-Layer Perceptron을 이용하면 해결가능
- Layer가 추가될 때마다 Decison Boundary(Linear Boundary)가 하나씩 추가되므로 분류하는 영역이 많아짐
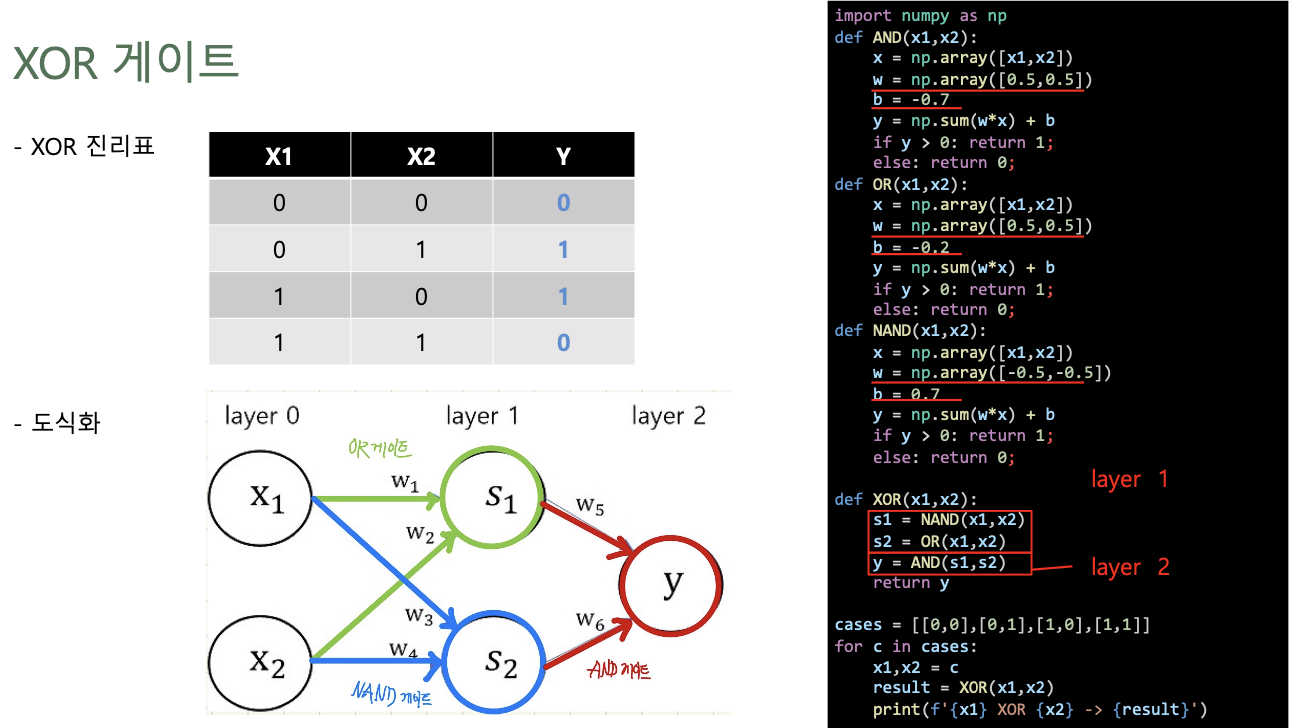
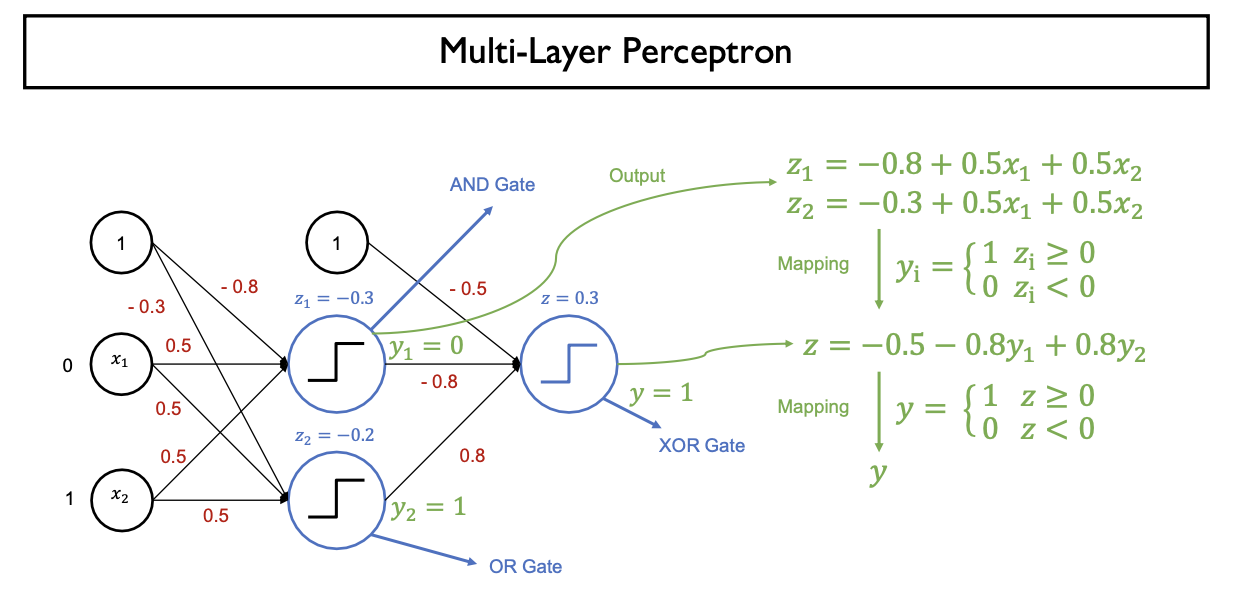
- 중간 hidden layer에 NAND, OR Gate 생성 -> Output을 AND Gate로 다시 입력으로 받아서 perceptron에 input
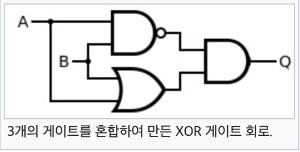
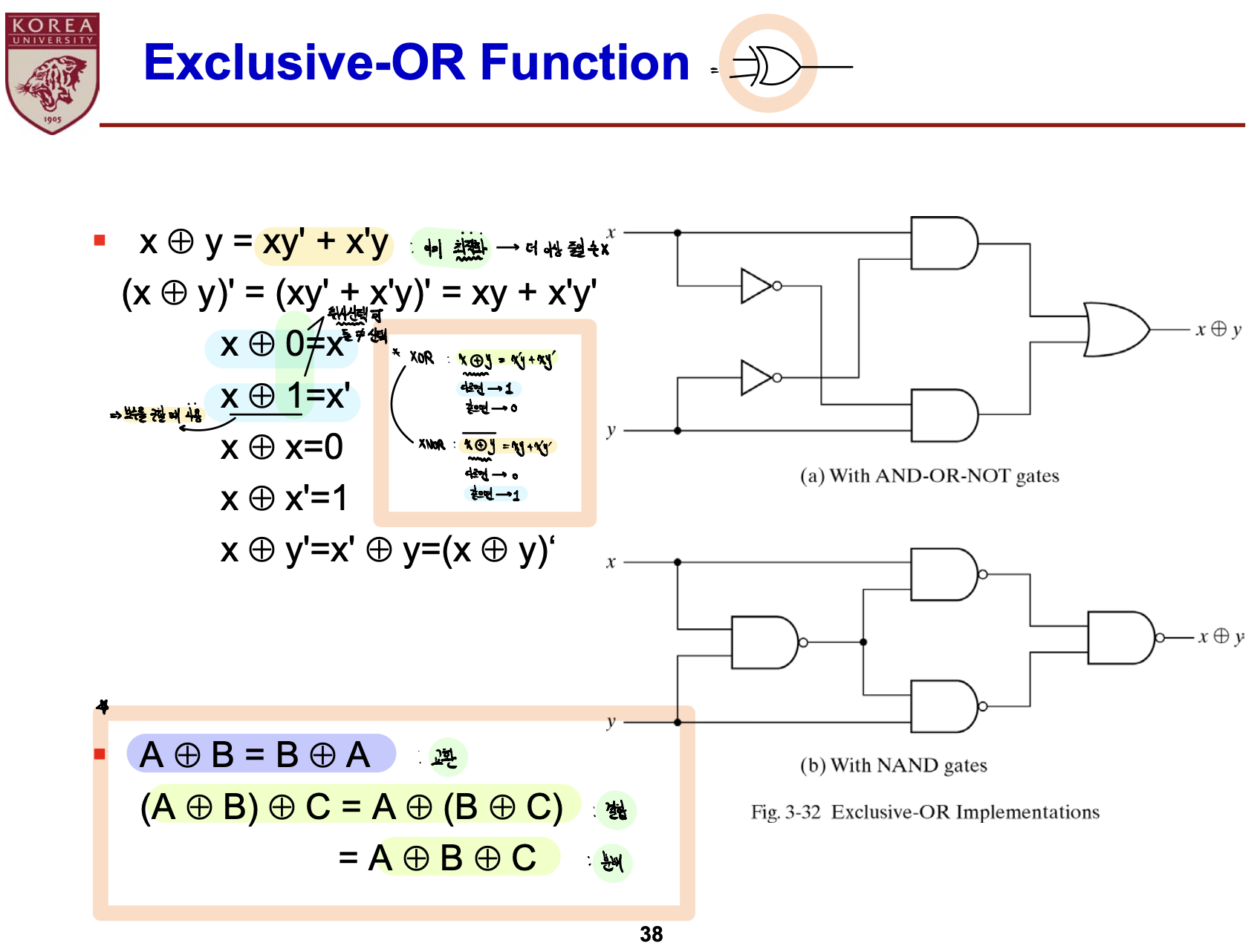
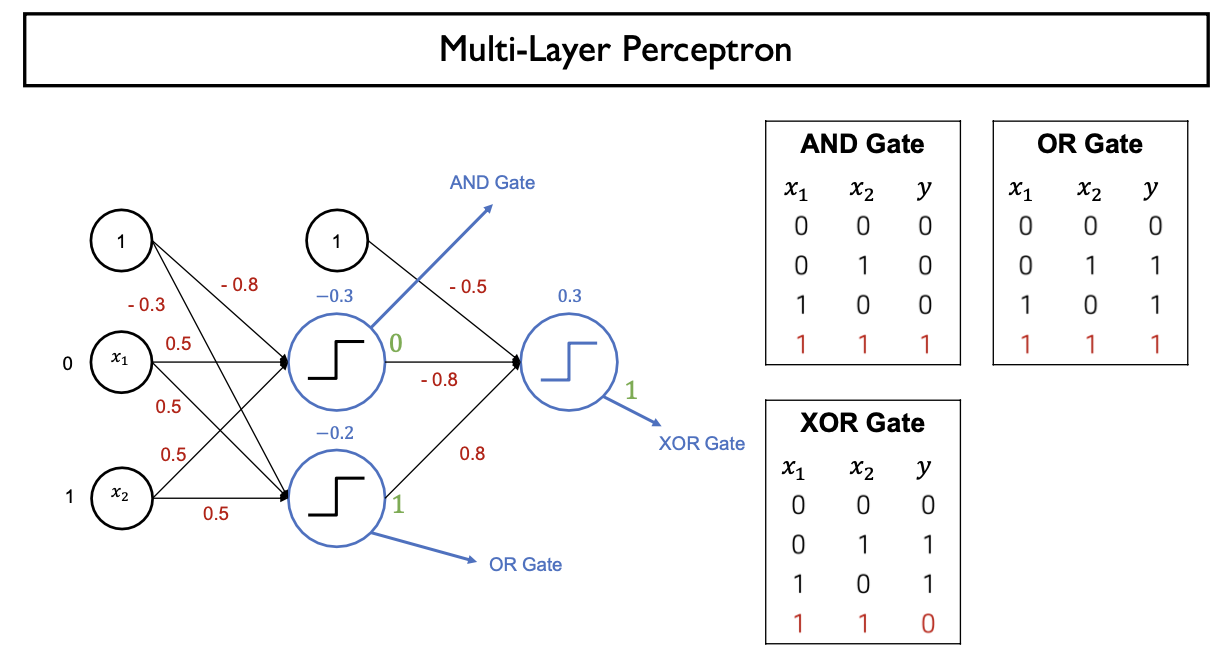
- X ⊕ Y = XY' + X'Y = (X+Y)(XY)' = (X+Y)(X'+Y')
- OR Gate와 NAND Gate를 AND Gate로 연결
- Truth Table을 통해 가능한 모든 X, Y Case에 대해 조사하면 Q.E.D
- X, Y가 서로 달라야 의미가 있음 -> X, Y가 다르면 1 같으면 0을 출력
3. MLP: Multi-Layer Perceptron
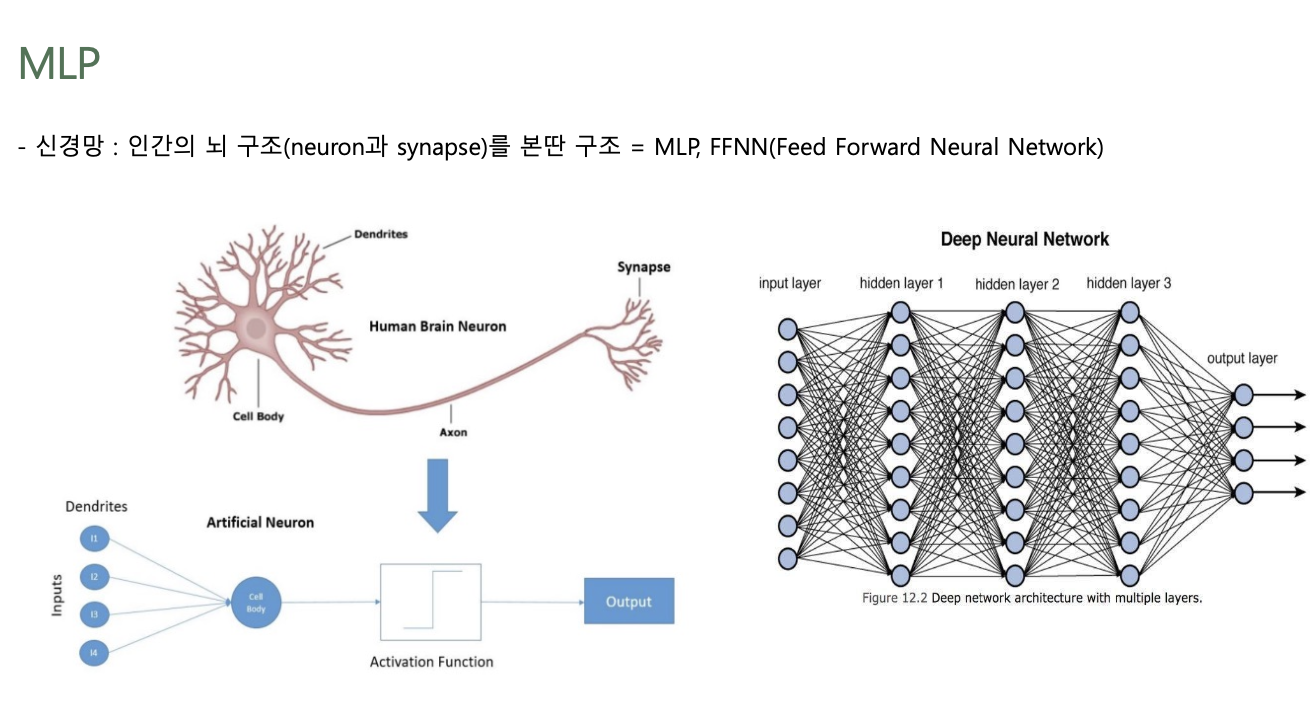
MLP
- Multi-Layer Perceptron
- 신경망: 인간의 뇌 구조(Neuron & Synapse)를 본딴 구조
- SLP과 다르게 Hidden Layer가 존재
- 여러 개의 Linear Boundary
- Non-Linear하게 분포하는 데이터에 대한 학습이 가능
Components of MLP (NN, FFNN)
- Input Layer
- Bias
- Hidden Layer
- Weight Matrix (Bias)
- Activation Function
- Output Layer
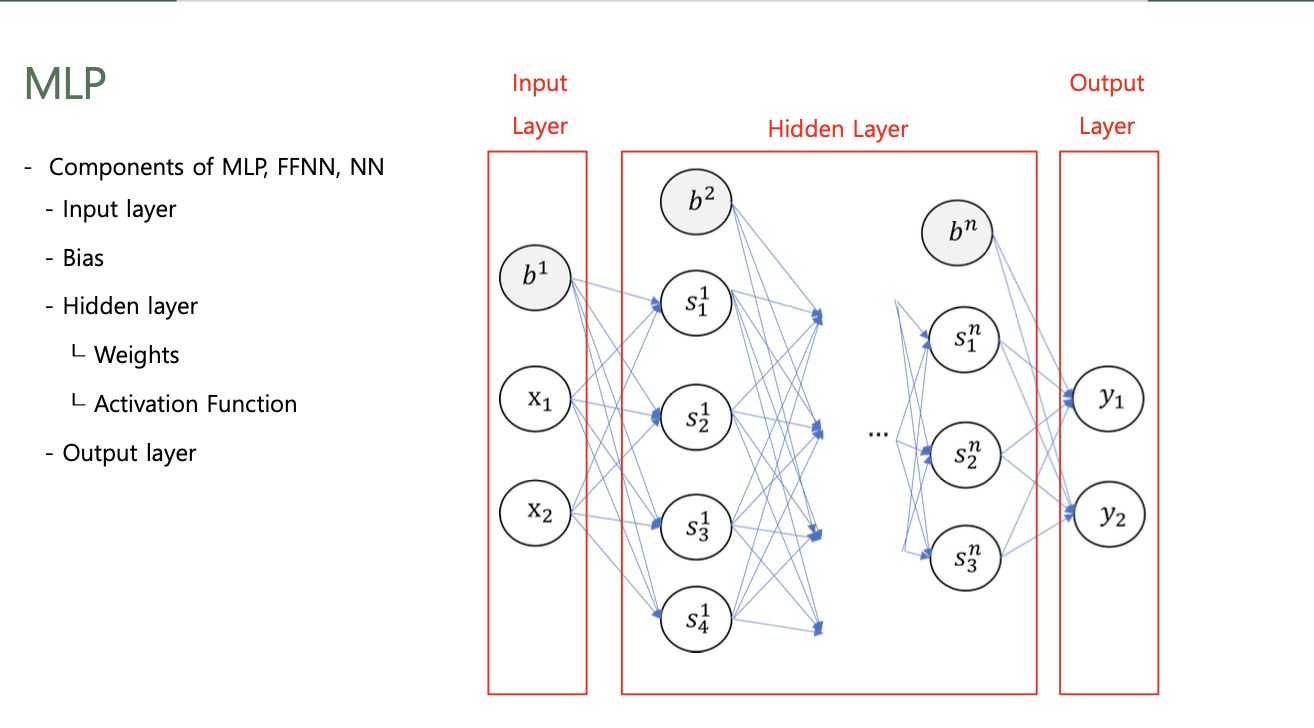
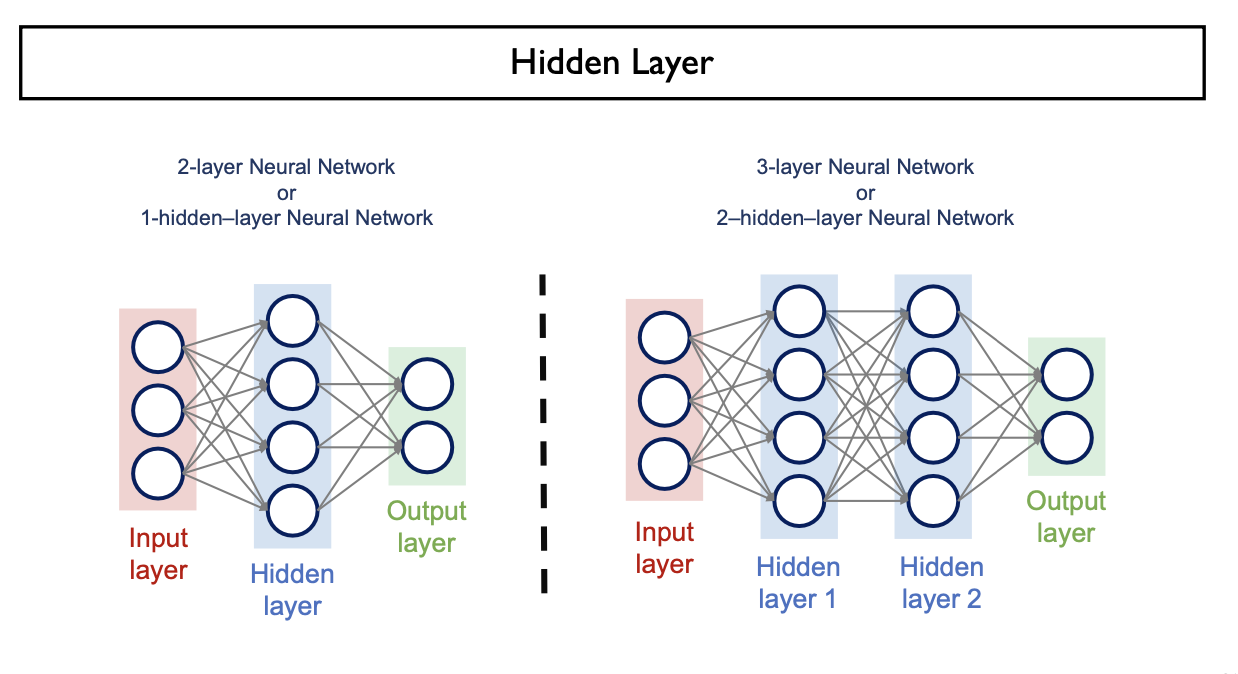
Hidden Layer
- Input Layer과 Output Layer 사이의 계층
- 순차적으로 연결하여 정보를 처리하는 neural network를 구성
- 굉장히 복잡한 task도 문제없이 수행해낼 수 있는 능력
일반적으로 Input Layer는 제공이 되기 때문에
Hidden Layer과 Output Layer의 개수를 세어 N-layer Neural Network라 한다
4. Forward Propagation (Feed Forward) / Backpropagation
- $a_{i} ^{(j)}$: $j$번째 Layer에 있는 $i$번째 노드의 Output (Activation Function의 결과값, 활성화함수 적용 후 Node)
- $W^{j}$: $j$번째 Layer에서 $j+1$번째 Layer으로 mapping하는 Weight Matrix
- $Z_{i} ^{(j)}$: $j$번째 Layer에 있는 $i$번째 노드 기준 Linear Combination

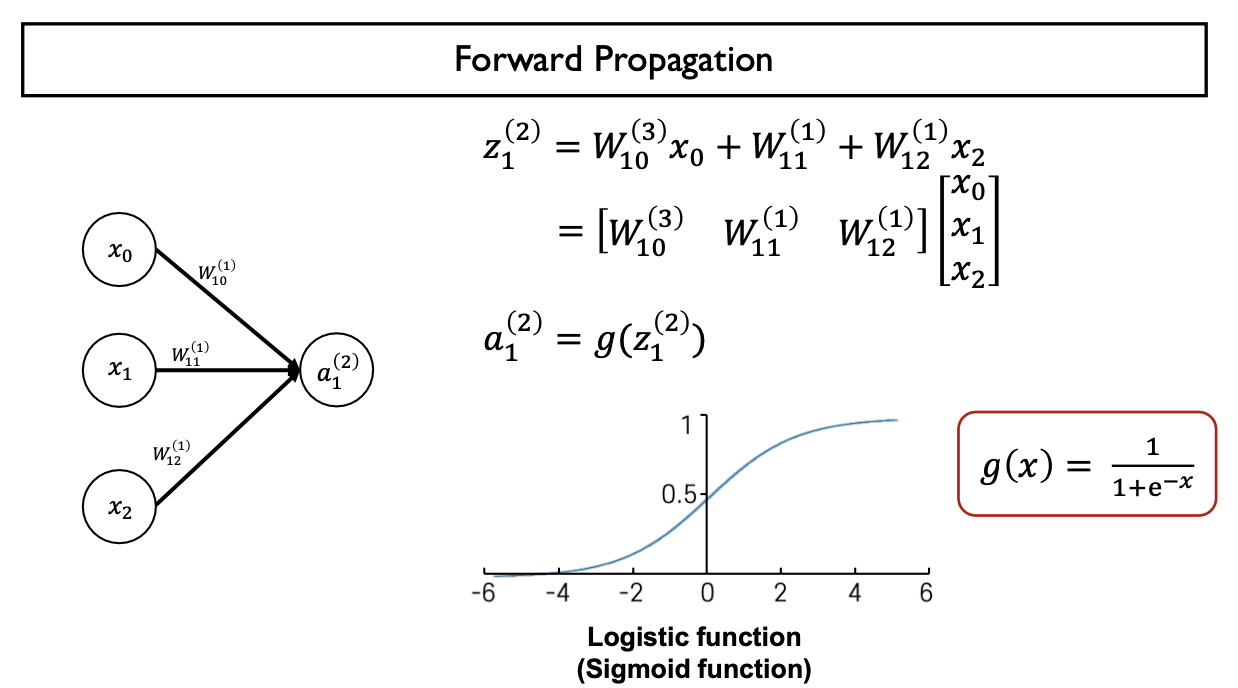
- Linear Combination (Input Feature & Model Parameter) -> Activation Function에 합성
- Output $a_{i} ^{(j)}$는 다시 Input Feature로 작용
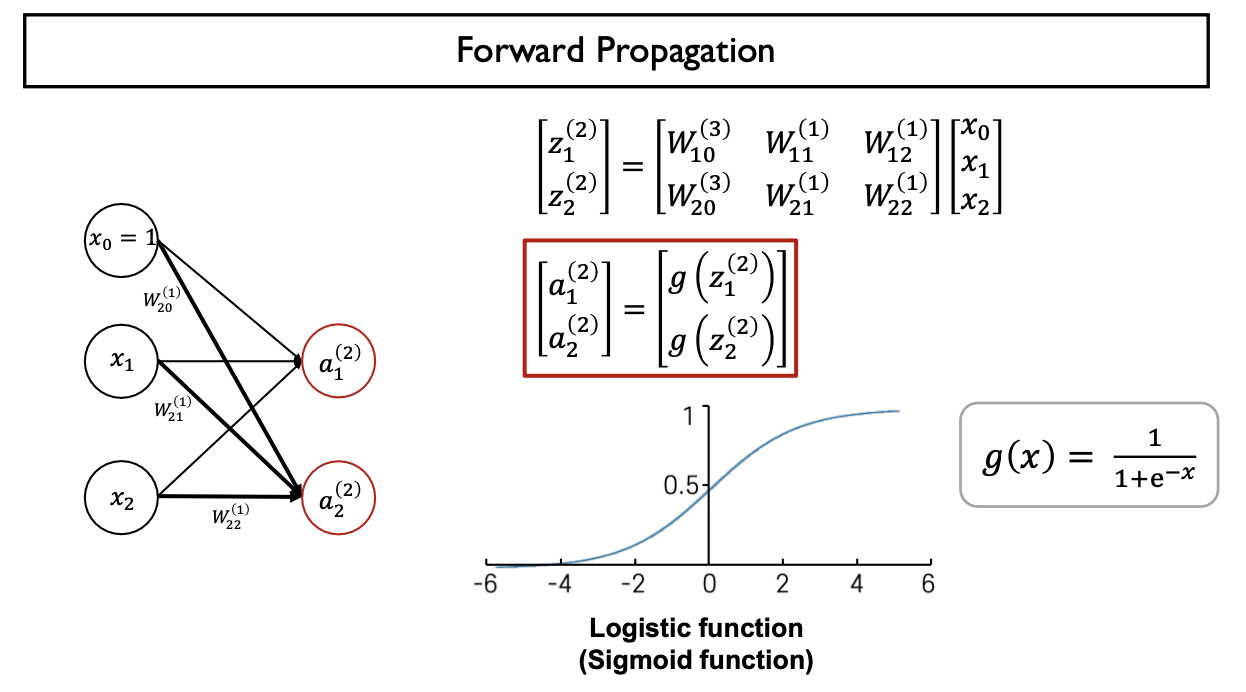
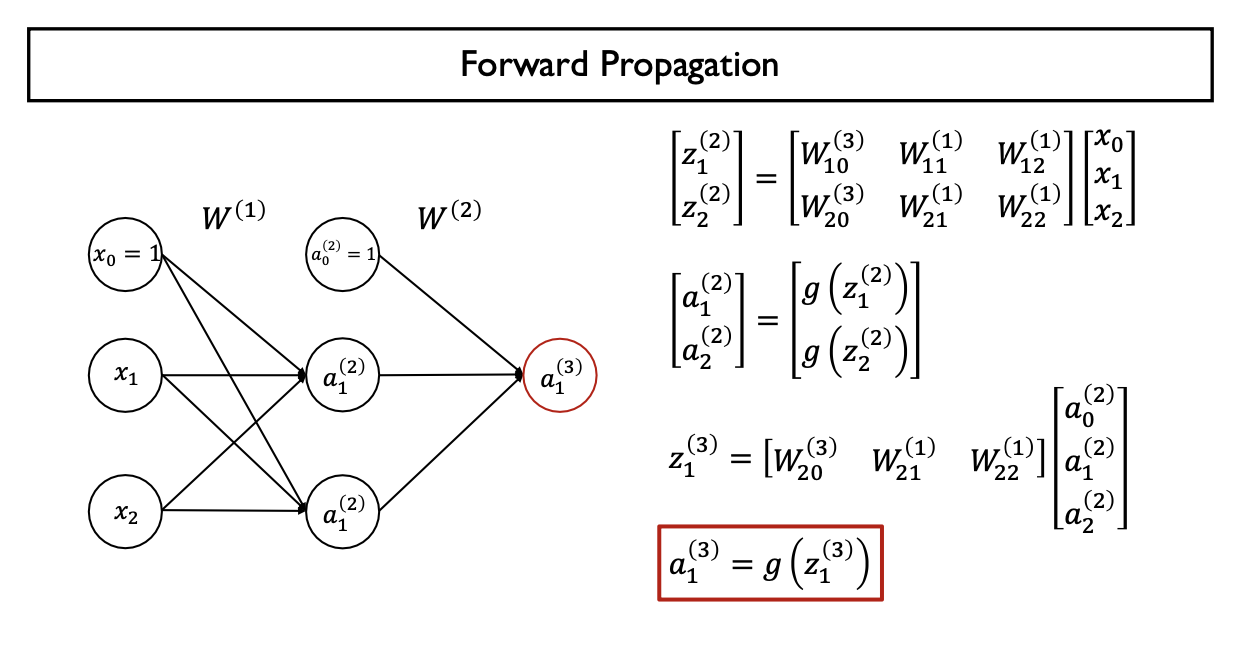
- Multi-Layer Perceptron의 각 layer별로 일어나는 계산과정을 이렇게 compact한 표현으로 나타냄
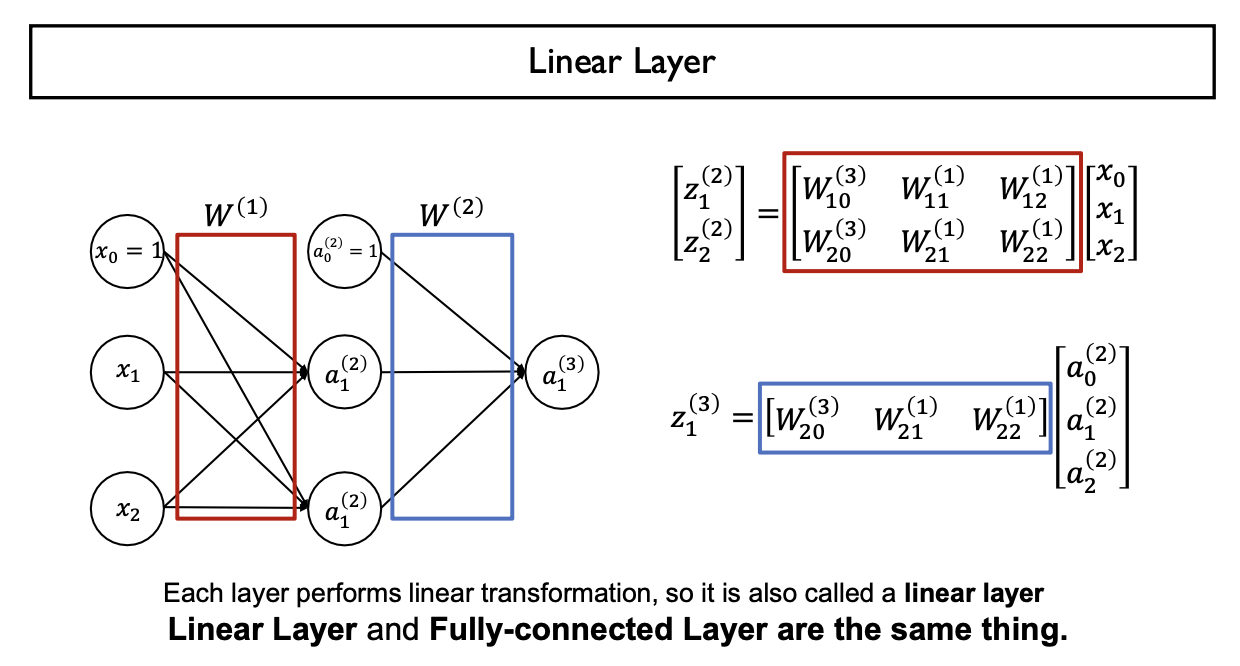
- 각 Layer는 Weight Matrix을 이용하여 j-th Layer에서 (j+1)-th Layer로 Mapping하는데, Linear Combination을 적용하므로 Linear Layer or Fully-Connected Layer이라 한다
Model Training
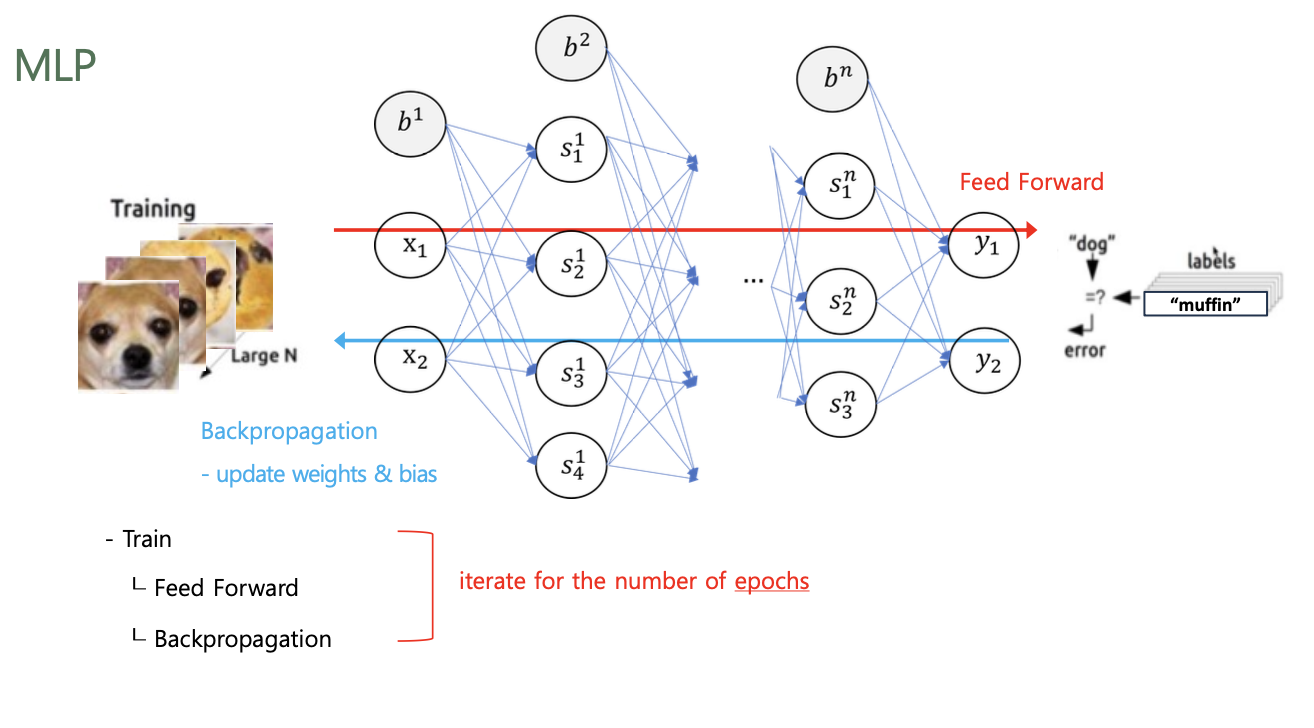
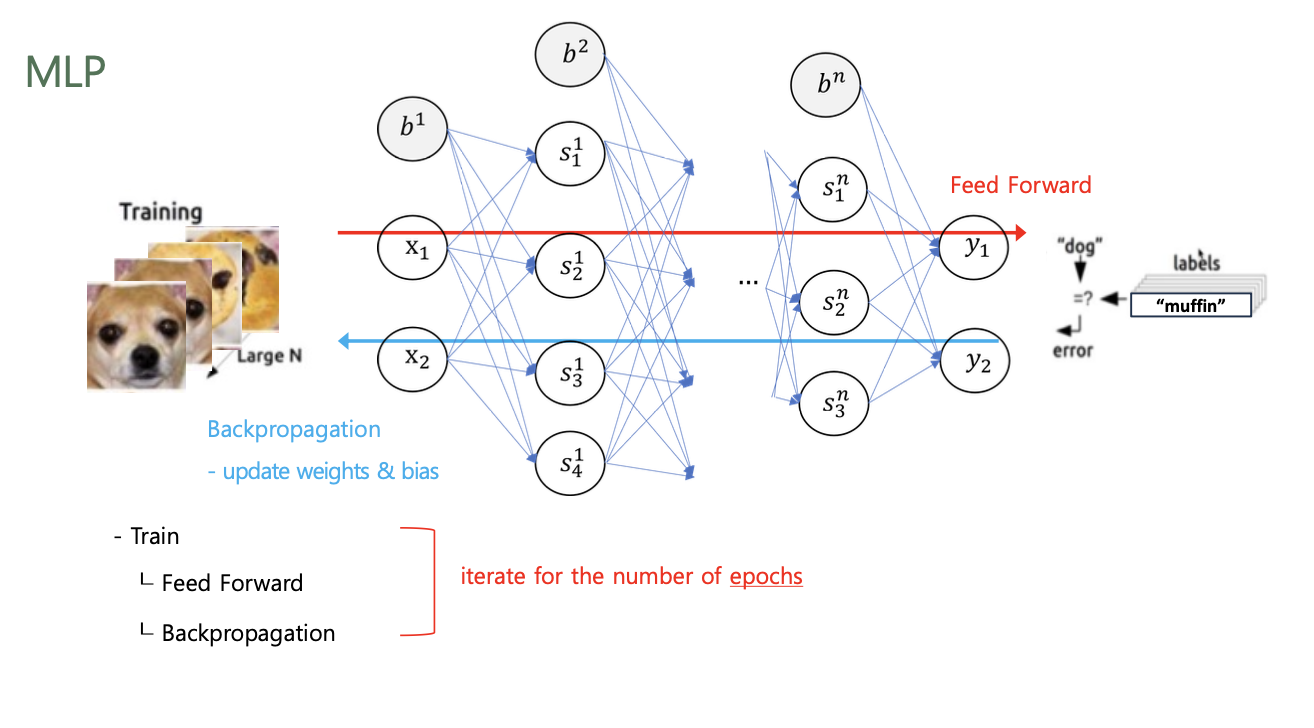
각 epoch 마다 Feed Forward / Backpropagation 수행
- Feed Forward (순전파)
- 입력 데이터를 기반으로 신경망을 따라 입력층(Input Layer)부터 출력층(Output Layer)까지 차례대로 변수들을 계산하고 추론(Inference)한 결과를 의미
- 모델(Model)에 입력값($x$)을 입력하여 순전파(Forward) 연산을 진행
- 이 과정에서 계층(Layer)마다 가중치(Weight)와 편향(Bias)으로 계산된 값이 활성화 함수(Activation Function)에 전달
- 최종 활성화 함수에서 출력값($ \hat{y}$)이 계산되고 이 값을 손실 함수(Loss Function)에 실젯값($y$)과 함께 연산하여 오차(Cost)를 계산
- Backpropagation (역전파)
- Input과 Output을 알고 있는 상태에서 신경망을 학습시키는 방법
- 순전파(Forward Propagation)의 방향과 반대로 연산이 진행
- 순전파(Forward Propagation) 과정을 통해 나온 오차(Cost)를 활용해 각 계층(Layer)의 가중치(Weight)와 편향(Bias)을 최적화
- 역전파 과정에서는 각각의 가중치와 편향을 최적화 하기 위해 연쇄 법칙(Chain Rule)을 활용
새로 계산된 가중치는 최적화(Optimization) 알고리즘을 통해
실젯값과 예측값의 차이를 계산하여 오차를 최소로 줄일 수 있는 가중치(Weight)와 편향(Bias)을 계산
5. Gradient Descent
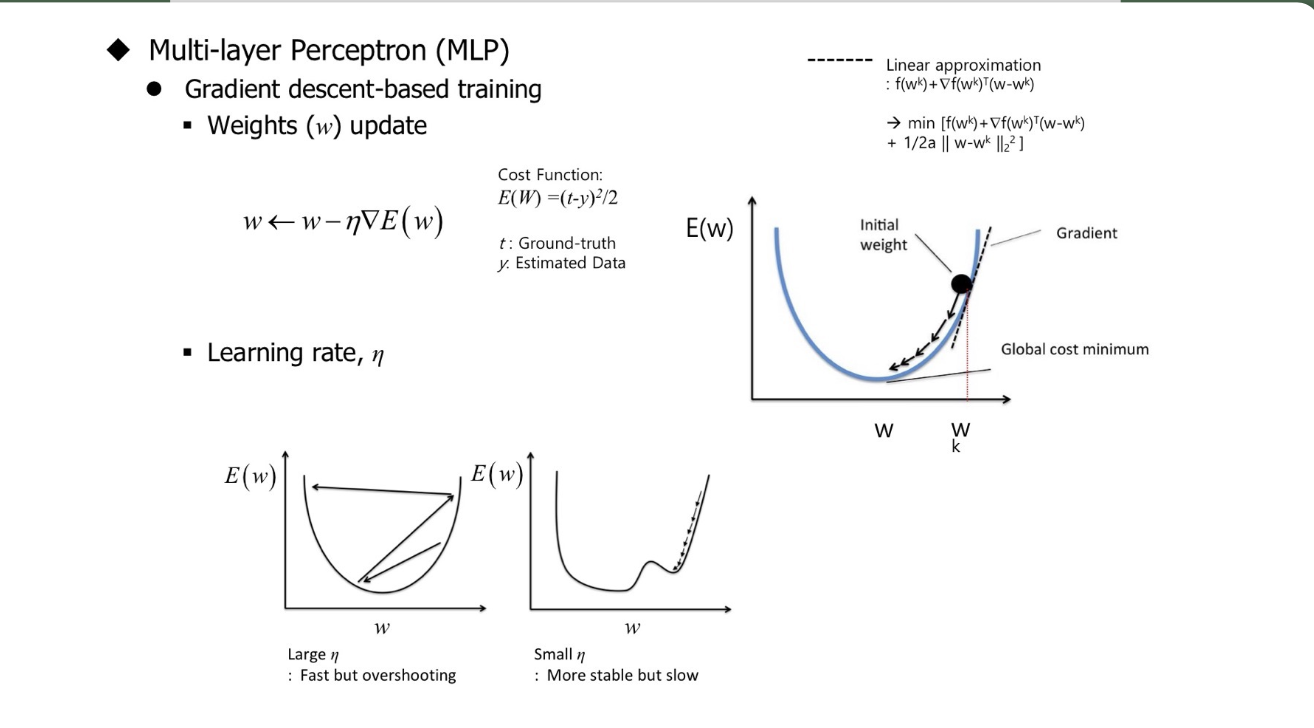
MLP - Gradient Descent-Based Training

다음의 Taylor's Theorem에 의해 1차항은 Gradient, 2차항은 Hessian Matrix를 이용해서 특정 $W^{k}$에서 근사한다
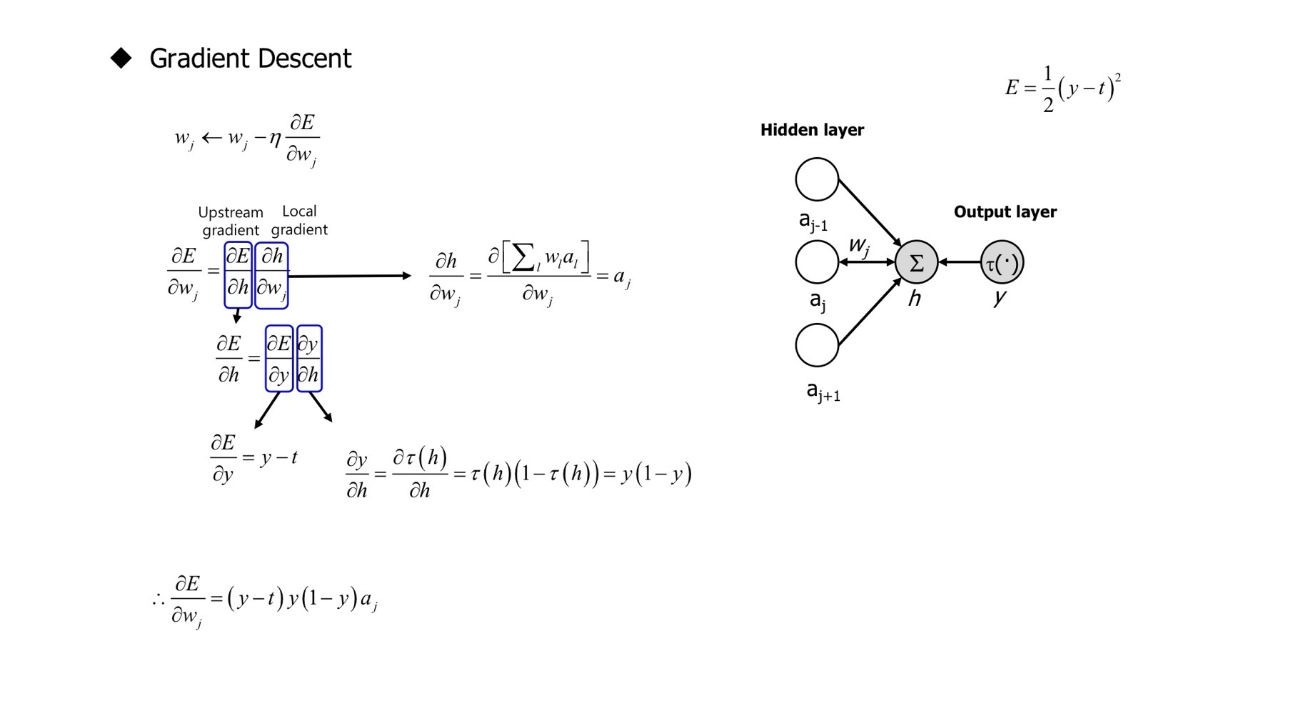
Gradient Descent Parameter Update - One Layer
Algorithm: $w_{j} \leftarrow w_{j} - \eta \frac{\partial E}{\partial w_{j}}$
$Total\; Gradient = Upstream \;Gradient \times Local \;Gradient$
$Upstream \; Gradient = \frac{\partial E}{\partial h} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial h} = (y - t) \times y(1-y)$
$Local \; Gradient = \frac{\partial h}{\partial w_{j}} = \frac{\partial \left [ \sum_{i}^{} a_{i}w_{i} \right ]}{\partial w_{j}} = a_{j}$
$\frac{\partial E}{\partial w_{j}} = \frac{\partial E}{\partial h} \frac{\partial h}{\partial w_{j}}$
$\therefore \frac{\partial E}{\partial w_{j}} = \frac{\partial E}{\partial h} \frac{\partial h}{\partial w_{j}} = (y-t)y(1-y)a_{j}$
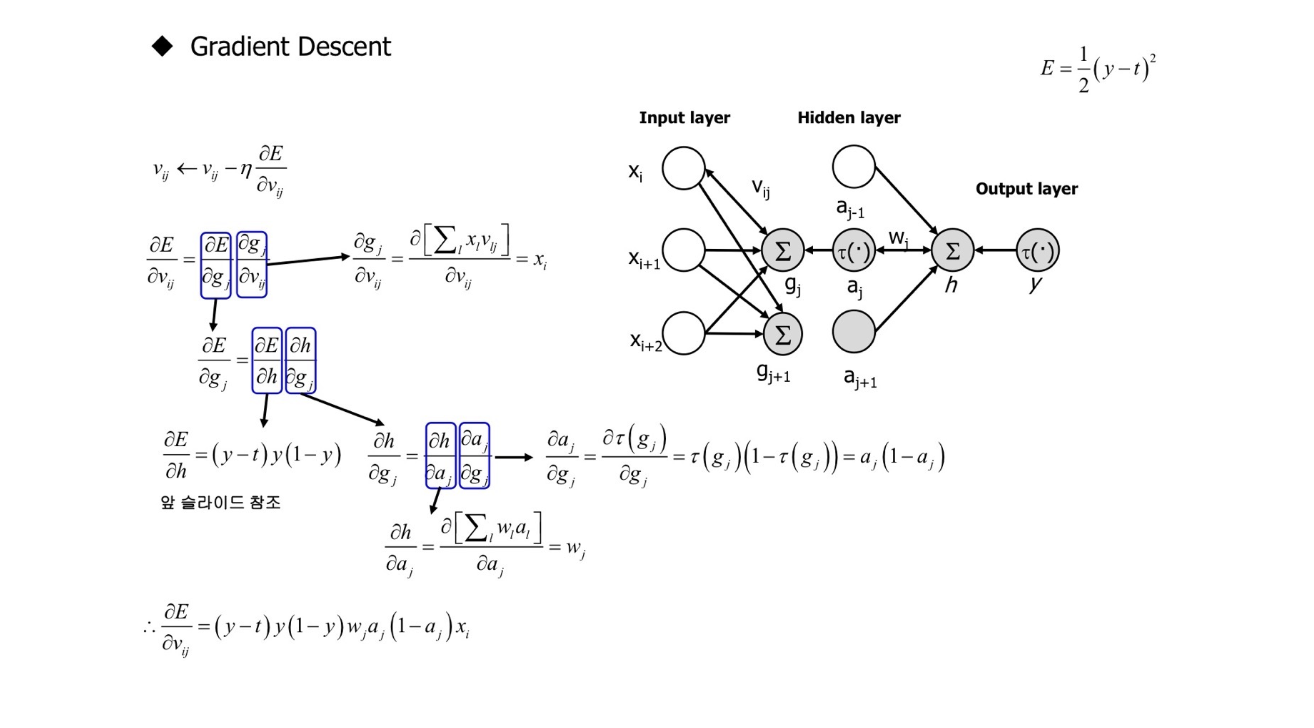
Gradient Descent Parameter Update - Two Layers
Algorithm: $\nu_{ij} \leftarrow \nu_{ij} - \eta \frac{\partial E}{\partial \nu_{ij}}$
$\frac{\partial E}{\partial \nu_{ij}} = \frac{\partial E}{\partial g_{j}}\frac{\partial g_{j}}{\partial \nu_{ij}}$
$=\left ( \frac{\partial E}{\partial h} \frac{\partial h}{\partial g_{j}} \right ) \left ( \frac{\partial \left [ \sum_{i}^{} x_{i}\nu_{ij} \right ]}{\partial \nu_{ij}} \right )$
$=\left ( \left ( (y-t)y(1-y) \right ) \left ( \frac{\partial h}{\partial a_{j}} \frac{\partial a_{j}}{\partial g_{j}} \right ) \right ) x_{i}$
$=\left ( \left ( (y-t)y(1-y) \right ) \left ( \frac{\partial \left [ \sum_{i}^{} w_{i}a_{i} \right ]}{\partial a_{j}} \left ( a_{j}(1-a_{j}) \right ) \right ) \right ) x_{i}$
$=\left ( \left ( (y-t)y(1-y) \right ) \left ( w_{j} \left ( a_{j}(1-a_{j}) \right ) \right ) \right ) x_{i}$
$\therefore \frac{\partial E}{\partial \nu_{ij}} = (y-t)y(1-y) w_{j} \left ( a_{j}(1-a_{j}) \right ) x_{i}$
6. Activation Function
Activation Function
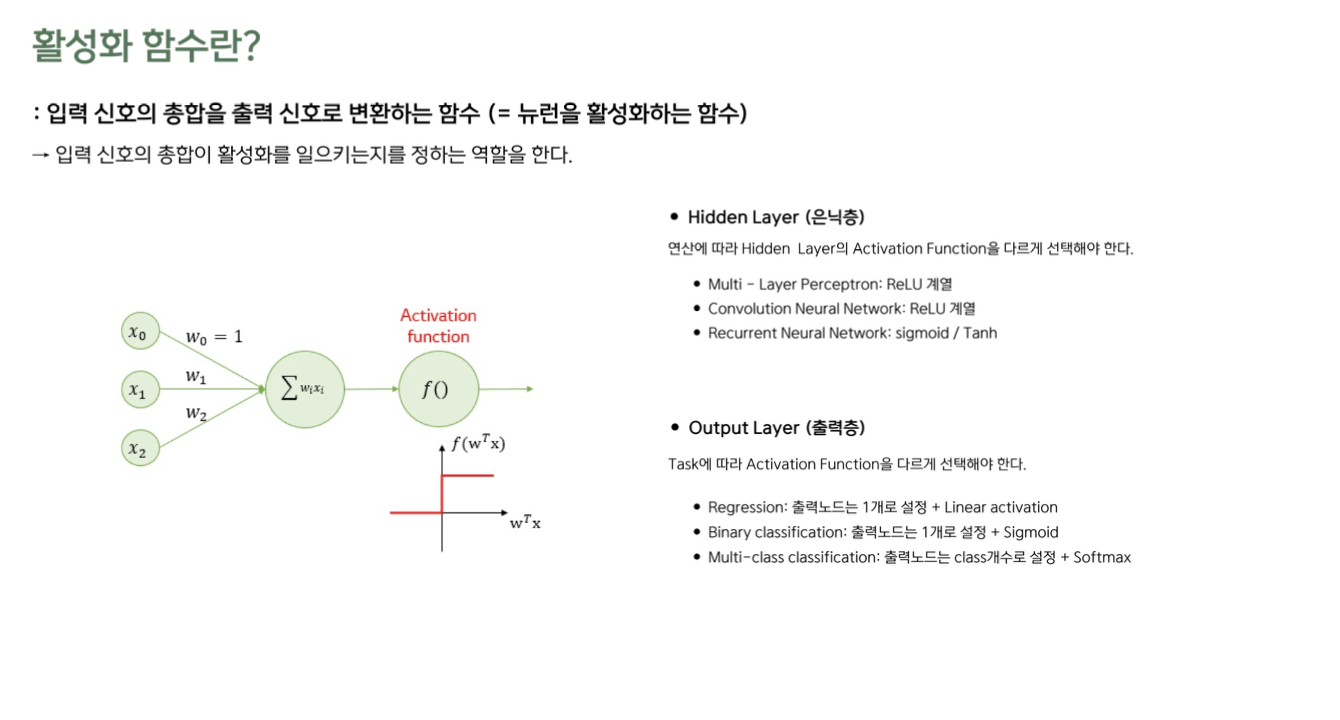
- 입력 신호의 총합을 출력 신호로 변환하는 함수 (= 뉴런을 활성화하는 함수)
- 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 한다
- Input: Input Vector(Feature) & Weight(Model Parameter)의 선형결합
- Hidden Layer과 Output Layer에 사용하는 Activation Function이 다르다
Hidden Layer Activation
- 연산에 따라 Hidden Layer의 Activation Functio이 다름
- MLP (Multi-Layer Perceptron): ReLU 계열
- CNN (Convolutional Neural Network): ReLU 계열
- RNN (Recurrent Neural Network): Sigmoid, Tanh
Output Layer Activation
- Task에 따라 Output Layer의 Activation Function이 다름
- Regression: 출력 노드 1개 + Linear Activation
- Binary Classification: 출력 노드 1개 + Sigmoid
- Multi-Class Classification: 출력 노드 Class 개수 + Softmax


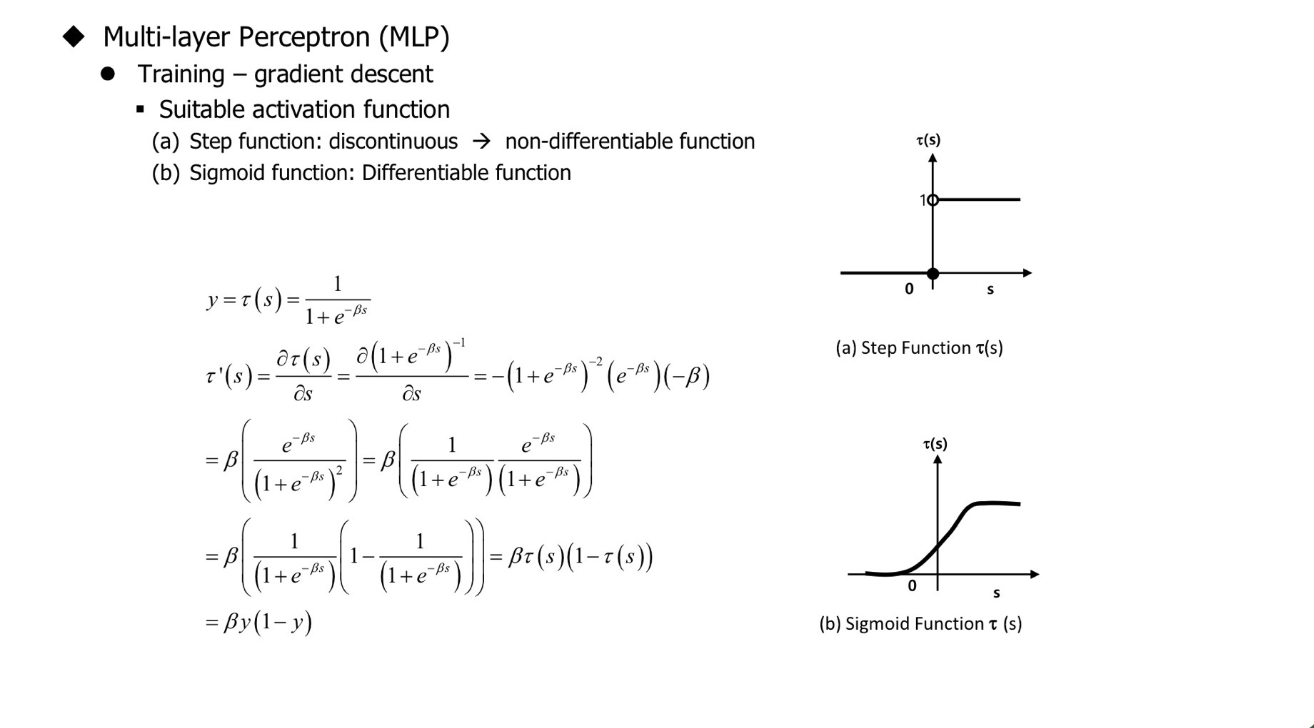
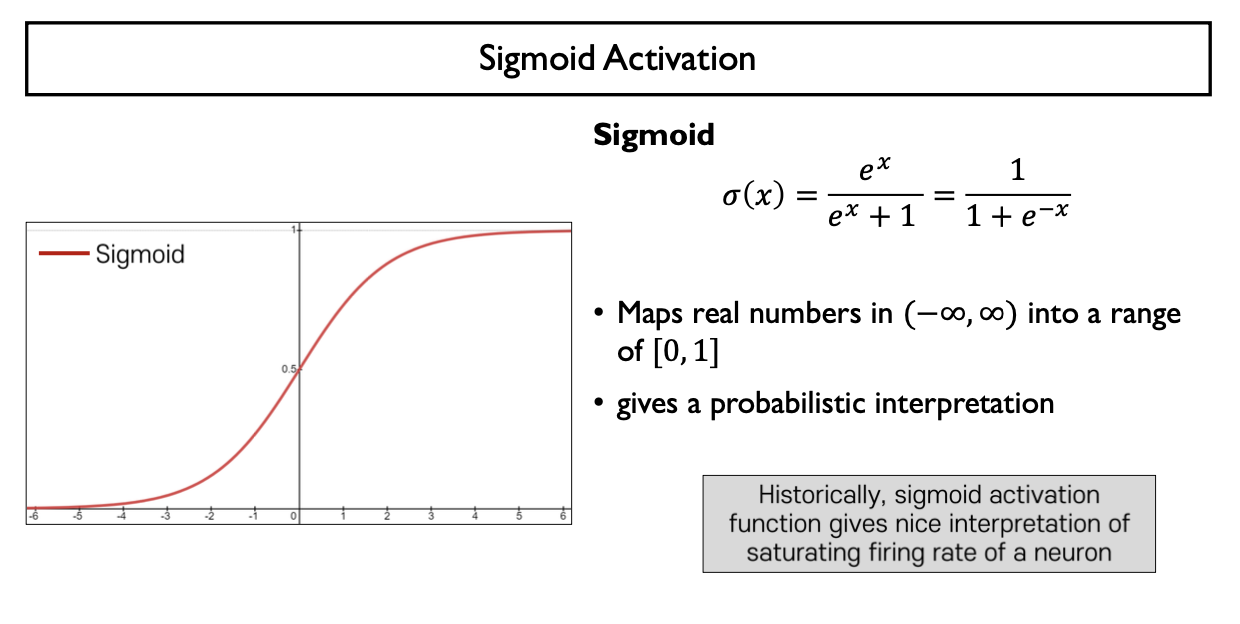
Sigmoid function
- 하나의 뉴런 or 퍼셉트론이 입력 신호를 선형결합하여 만든 값에 hard threshold(Step Function)를 부드러운 형태의 곡선으로 근사
- 실수 전체의 값을 (0,1) 사이의 실수 값으로 mapping
- logistic regression의 경우 positive class에 대응하는 확률 값으로 해석
- np.exp(-x) : $e^{-x}$
e ** (-x)np.exp ** (-x)
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
#그래프 그러보기
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()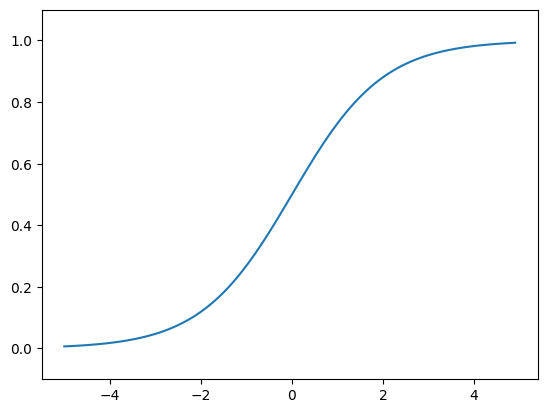
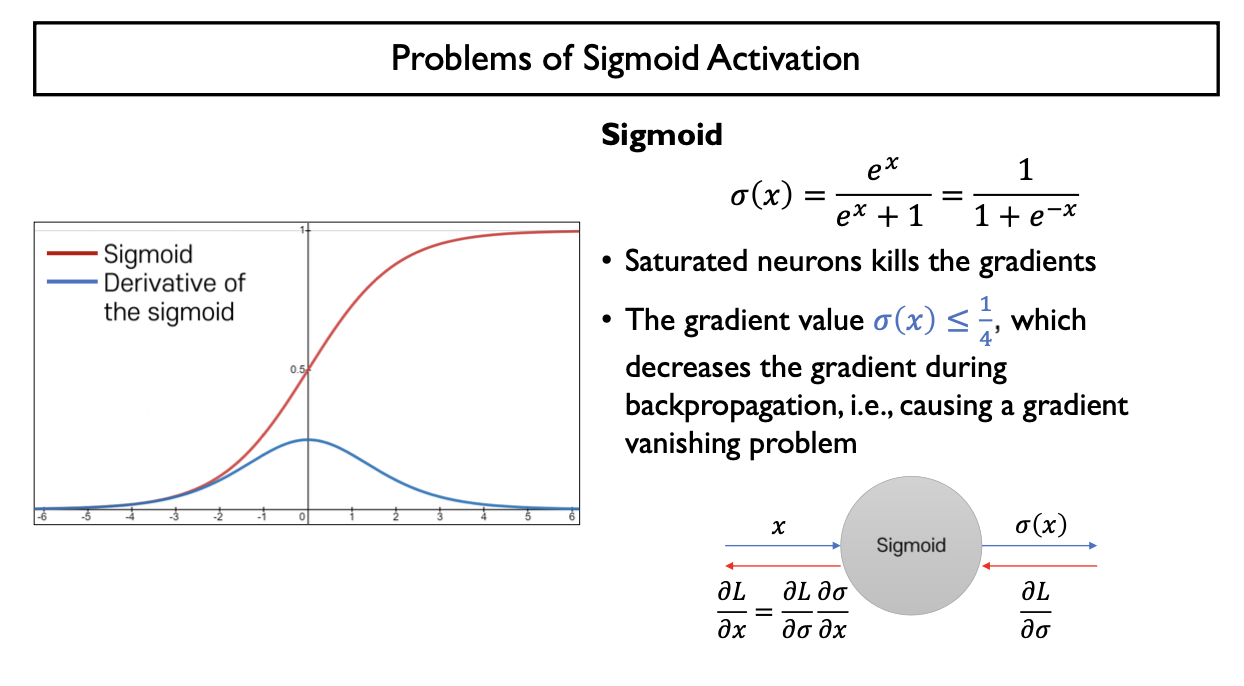
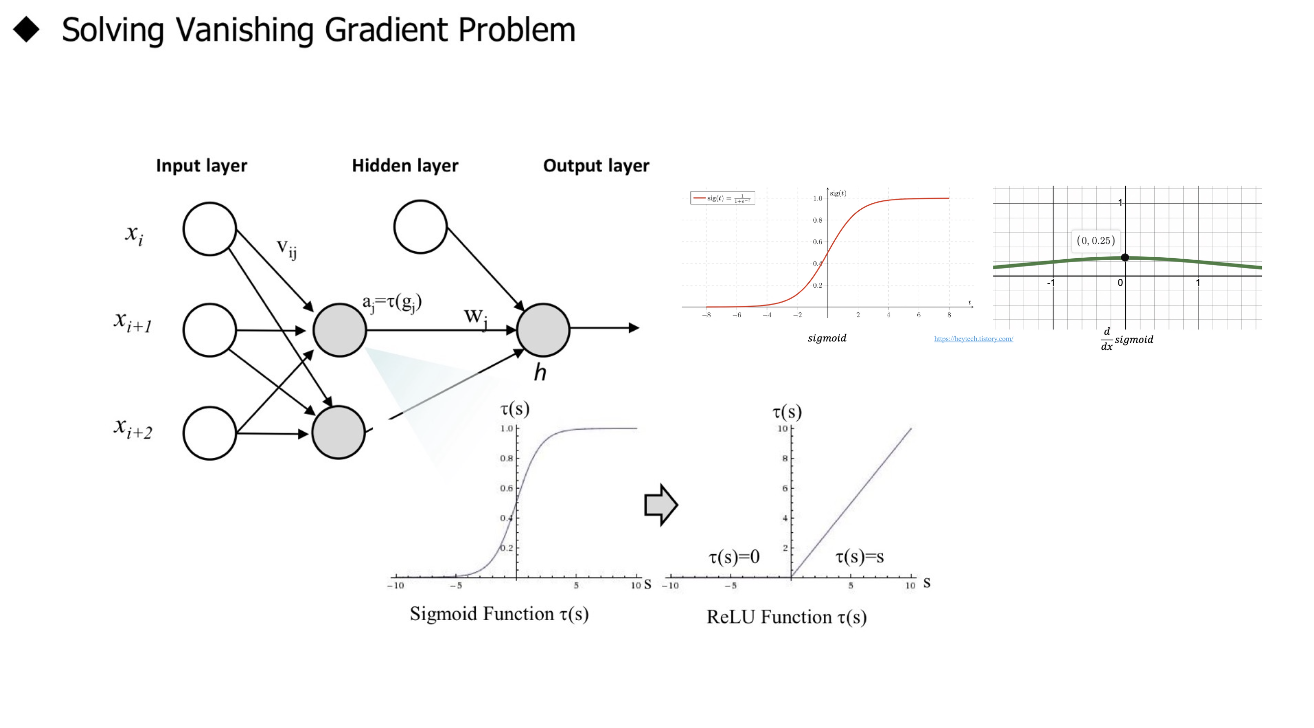
Gradient Vanishing Problem
- $ 0 < \frac{\partial \sigma (x)}{\partial x} = (1-\sigma(x))\sigma(x) \leq \frac {1} {4}, 0<\sigma(x) <1 $, 즉 Gradient의 범위가 $(0, \frac {1} {4}]$ 이므로 Backpropagtion 할 때마다 Gradient값이 점차 작아지는 양상을 보임
- multi-layer neural network에서 sigmoid function의 backpropgation을 수행할 때마다 gradient 값이 0에 수렴
- 앞쪽의 layer의 parameter에 도달하는 gradient 값이 굉장히 작음: 앞쪽의 parameter들의 update가 거의 일어나지 않음
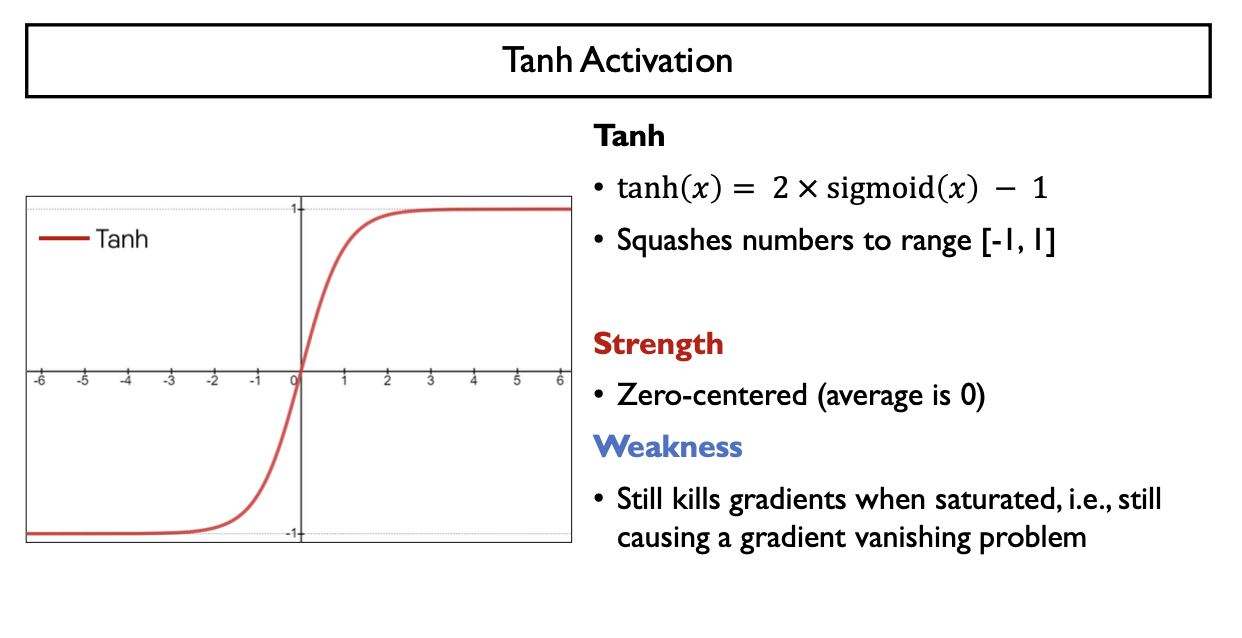
Tanh Activation
- $tahh(x) = 2 \times sigmoid(2x) -1 = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}$
- Sigmoid 함수를 x축으로 $\frac {1} {2}$배 압축 & y축으로 2배 확대 -> y축으로 -1만큼 평행이동
- 치역의 범위가 (-1,1)으로 한정
- Strength
- Zero-centered (average = 0)
- Weakness
- gradient의 범위가 $0< \frac{\partial tanh(x)}{\partial x} = 1 - tanh(x)^{2} = (1+tanh(x))(1-tanh(x)) \leq 1$, $(0,1]$
- backpropagation할 때마다 gradient vanishing 문제를 여전히 가지게 됨
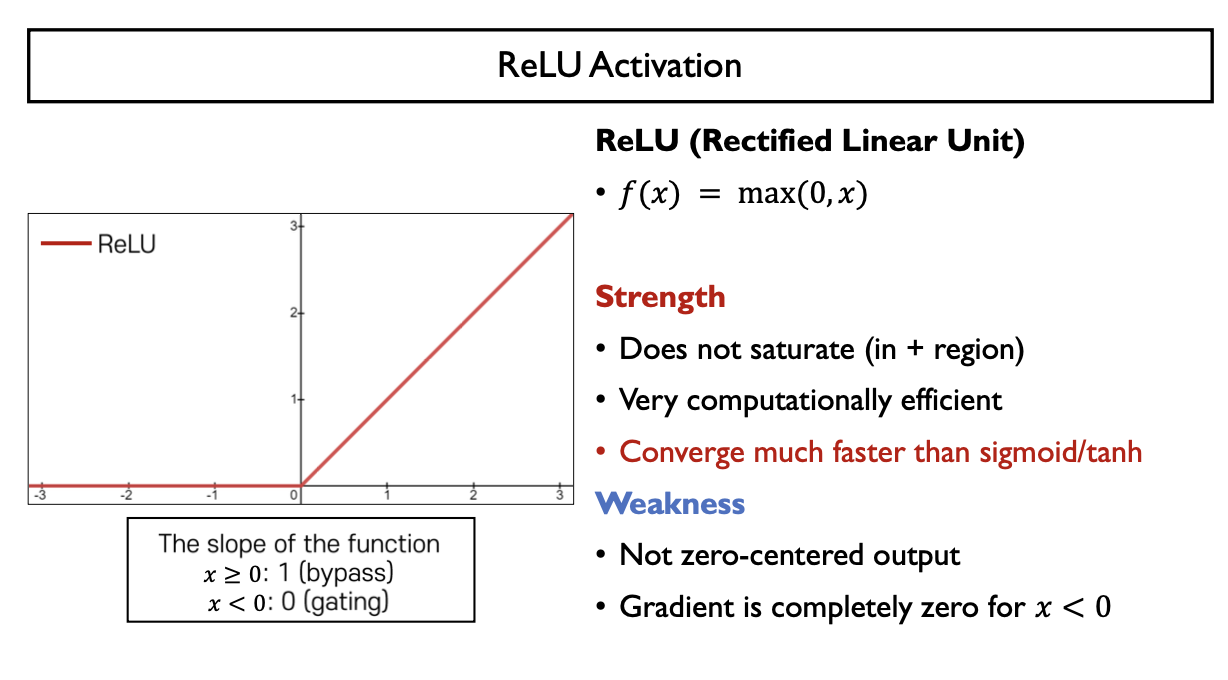
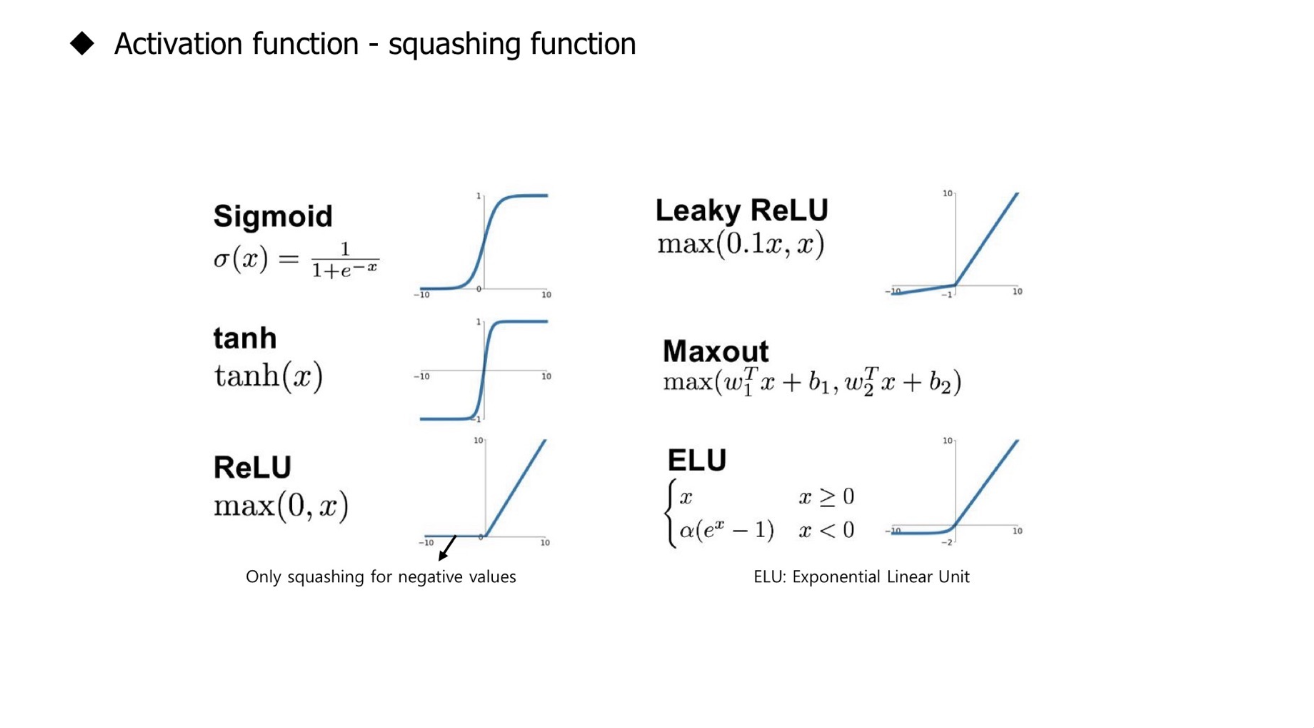
RELU Activation (Rectified Linear Unit)
- $f(x) = max(0,x)$
- Strength
- gradient vanishing 문제를 해결 (gradient 값이 계속 1)
- 다른 활성함수에 비해 간단한 연산: computationally efficient
- Weakness
- Not zero-centered output
- 음수 범위에서는 gradient 값이 0: 이후의 gradient가 모두 0이 되는 문제

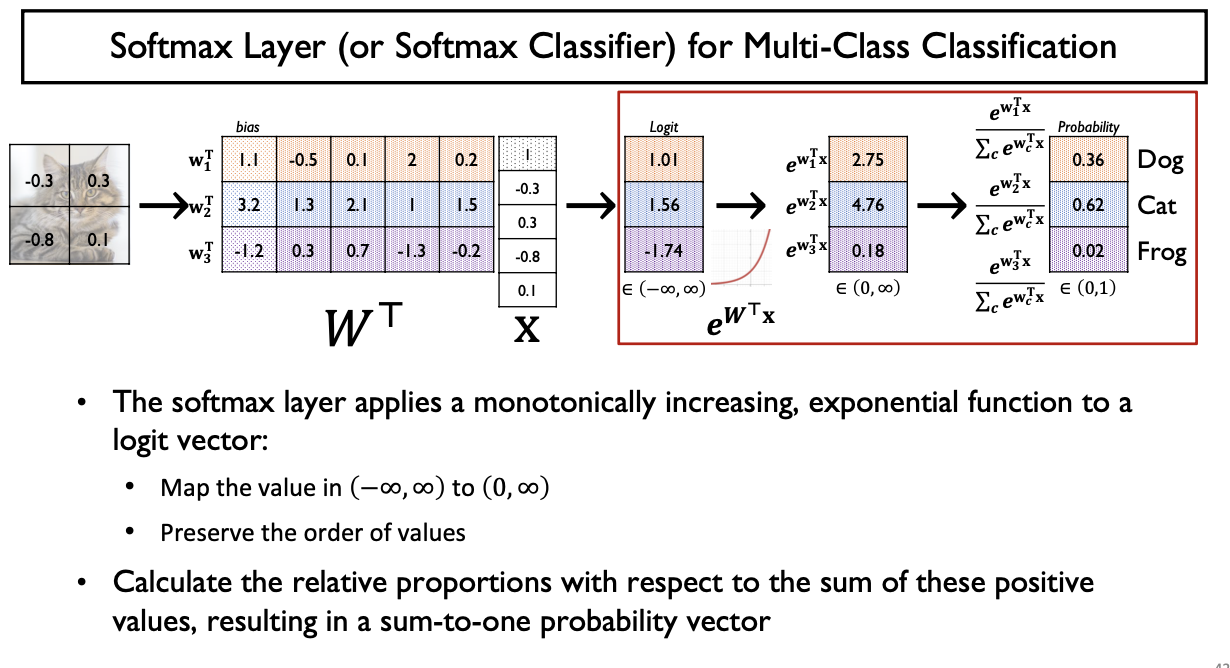
Softmax Activation Function
Multi-Class Classification에서
output vector의 형태가 총합이 1이고
각각 [0, 1] 사이의 확률분포를 가지는 activation function을 softmax layer 이라 한다
- 소프트맥스(softmax) 함수는 모델의 출력을 확률로 해석할 수 있게 변환해 주는 연산
- 분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측
1. Machine Learning & Deep Learning
AI (Artificial Intelligence)
- 지능형 기계를 만드는 과학이나 공학의 분야 / 인간의 지능(지적능력, 사고방식) 을 인공적으로 컴퓨터 시스템을 통해 구현한 것
ML (Machine Learning)
- 입력 데이터가 주어졌을 때 답을 유추해 줄 수 있는 최적의 함수를 기계가 찾는 것
- 기존 데이터에 알고리즘을 사용해 모델을 만들어내고, 새로운 데이터에 해당 모델을 적용시켜 패턴을 학습하고 결과를 추론하는 기법
- 데이터를 기반으로 통계적인 신뢰도를 강화
- 예측 오류를 최소화하기 위해 다양한 수학적 기법을 사용
- 데이터 내의 패턴을 스스로 인지하고 신뢰도있는 예측결과를 도출해 내는 함수를 찾는 것

- 머신러닝 개요

DL (Deep Learning)
- 머신러닝의 방법론 중 하나 (비선형 정보처리를 수행하는 계층을 여러 겹으로 쌓아서 학습모델을 구현하는 머신러닝의 한 분야)
- 엄청나게 많은 데이터에서 중요한 패턴을 잘 찾아냄, 규칙도 잘 찾아내고, 의사결정을 잘하게 됨

2. Perceptron
Perceptron
- 다수의 신호를 입력받아 하나의 신호를 출력하는 알고리즘
- 가장 단순한 형태의 신경망(Neural Network): Single Layer Perceptron

Components of Perceptron
- Input Features(Input Vectors):
- Model Parameters(Weight):
- Linear Combination:
- Activation Function:
- Output:




Logic Gates w/ Perceptron
Single Layer Perceptron(w/ Hard thresholding function)은 Linear Problem (Linear Model)만 해결가능 (구현가능)
Non-Linear Problem (Non-Linear Model)을 어떻게 해결(구현) 하는가?
- 고차원 항을 추가: Kernel Perceptron (커널화된 퍼셉트론)을 사용
- 다계층을 활용 (XOR Problem)
Logic Gates
- AND: 둘 다 1이여야만 1 (곱한다고 생각)
- OR: 둘 중 하나만 1이면 1 (더한다고 생각, 1 OR 1 = 1에 주의)
- NAND: AND Gate출력에 NOT Gate 처리
- NOR: OR Gate 출력에 NOT Gate 처리

- NAND, NOR Gate 보충설명




- NAND, NOR: Invertor로 작동하도록 설계 가능

- Decision Boundary

- AND, OR Gate 구현 (single layer perceptron)
- Model parameter (가중치 weight)을 적절하게 조정하여 AND, OR Gate 모두 설계가능
- Single layer perceptron은 only linear problem만 해결가능




- XOR Gate 구현 (MLP 이용)
- Multi-Layer Perceptron을 이용하면 해결가능
- Layer가 추가될 때마다 Decison Boundary(Linear Boundary)가 하나씩 추가되므로 분류하는 영역이 많아짐
- 중간 hidden layer에 NAND, OR Gate 생성 -> Output을 AND Gate로 다시 입력으로 받아서 perceptron에 input
- X ⊕ Y = XY' + X'Y = (X+Y)(XY)' = (X+Y)(X'+Y')
- OR Gate와 NAND Gate를 AND Gate로 연결
- Truth Table을 통해 가능한 모든 X, Y Case에 대해 조사하면 Q.E.D
- X, Y가 서로 달라야 의미가 있음 -> X, Y가 다르면 1 같으면 0을 출력







3. MLP: Multi-Layer Perceptron
MLP
- Multi-Layer Perceptron
- 신경망: 인간의 뇌 구조(Neuron & Synapse)를 본딴 구조
- SLP과 다르게 Hidden Layer가 존재
- 여러 개의 Linear Boundary
- Non-Linear하게 분포하는 데이터에 대한 학습이 가능

Components of MLP (NN, FFNN)
- Input Layer
- Bias
- Hidden Layer
- Weight Matrix (Bias)
- Activation Function
- Output Layer

Hidden Layer
- Input Layer과 Output Layer 사이의 계층
- 순차적으로 연결하여 정보를 처리하는 neural network를 구성
- 굉장히 복잡한 task도 문제없이 수행해낼 수 있는 능력
일반적으로 Input Layer는 제공이 되기 때문에
Hidden Layer과 Output Layer의 개수를 세어 N-layer Neural Network라 한다



4. Forward Propagation (Feed Forward) / Backpropagation


- Linear Combination (Input Feature & Model Parameter) -> Activation Function에 합성
- Output


- Multi-Layer Perceptron의 각 layer별로 일어나는 계산과정을 이렇게 compact한 표현으로 나타냄
- 각 Layer는 Weight Matrix을 이용하여 j-th Layer에서 (j+1)-th Layer로 Mapping하는데, Linear Combination을 적용하므로 Linear Layer or Fully-Connected Layer이라 한다

Model Training
각 epoch 마다 Feed Forward / Backpropagation 수행
- Feed Forward (순전파)
- 입력 데이터를 기반으로 신경망을 따라 입력층(Input Layer)부터 출력층(Output Layer)까지 차례대로 변수들을 계산하고 추론(Inference)한 결과를 의미
- 모델(Model)에 입력값(
- 이 과정에서 계층(Layer)마다 가중치(Weight)와 편향(Bias)으로 계산된 값이 활성화 함수(Activation Function)에 전달
- 최종 활성화 함수에서 출력값(
- Backpropagation (역전파)
- Input과 Output을 알고 있는 상태에서 신경망을 학습시키는 방법
- 순전파(Forward Propagation)의 방향과 반대로 연산이 진행
- 순전파(Forward Propagation) 과정을 통해 나온 오차(Cost)를 활용해 각 계층(Layer)의 가중치(Weight)와 편향(Bias)을 최적화
- 역전파 과정에서는 각각의 가중치와 편향을 최적화 하기 위해 연쇄 법칙(Chain Rule)을 활용
새로 계산된 가중치는 최적화(Optimization) 알고리즘을 통해
실젯값과 예측값의 차이를 계산하여 오차를 최소로 줄일 수 있는 가중치(Weight)와 편향(Bias)을 계산

5. Gradient Descent
MLP - Gradient Descent-Based Training

다음의 Taylor's Theorem에 의해 1차항은 Gradient, 2차항은 Hessian Matrix를 이용해서 특정

Gradient Descent Parameter Update - One Layer
Algorithm:

Gradient Descent Parameter Update - Two Layers
Algorithm:

6. Activation Function
Activation Function
- 입력 신호의 총합을 출력 신호로 변환하는 함수 (= 뉴런을 활성화하는 함수)
- 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 한다
- Input: Input Vector(Feature) & Weight(Model Parameter)의 선형결합
- Hidden Layer과 Output Layer에 사용하는 Activation Function이 다르다

Hidden Layer Activation
- 연산에 따라 Hidden Layer의 Activation Functio이 다름
- MLP (Multi-Layer Perceptron): ReLU 계열
- CNN (Convolutional Neural Network): ReLU 계열
- RNN (Recurrent Neural Network): Sigmoid, Tanh
Output Layer Activation
- Task에 따라 Output Layer의 Activation Function이 다름
- Regression: 출력 노드 1개 + Linear Activation
- Binary Classification: 출력 노드 1개 + Sigmoid
- Multi-Class Classification: 출력 노드 Class 개수 + Softmax


Sigmoid function
- 하나의 뉴런 or 퍼셉트론이 입력 신호를 선형결합하여 만든 값에 hard threshold(Step Function)를 부드러운 형태의 곡선으로 근사
- 실수 전체의 값을 (0,1) 사이의 실수 값으로 mapping
- logistic regression의 경우 positive class에 대응하는 확률 값으로 해석

- np.exp(-x) :
e ** (-x)np.exp ** (-x)
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
#그래프 그러보기
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
Gradient Vanishing Problem
- multi-layer neural network에서 sigmoid function의 backpropgation을 수행할 때마다 gradient 값이 0에 수렴
- 앞쪽의 layer의 parameter에 도달하는 gradient 값이 굉장히 작음: 앞쪽의 parameter들의 update가 거의 일어나지 않음



Tanh Activation
- Sigmoid 함수를 x축으로
- 치역의 범위가 (-1,1)으로 한정
- Strength
- Zero-centered (average = 0)
- Weakness
- gradient의 범위가
- backpropagation할 때마다 gradient vanishing 문제를 여전히 가지게 됨
- gradient의 범위가

RELU Activation (Rectified Linear Unit)
- Strength
- gradient vanishing 문제를 해결 (gradient 값이 계속 1)
- 다른 활성함수에 비해 간단한 연산: computationally efficient
- Weakness
- Not zero-centered output
- 음수 범위에서는 gradient 값이 0: 이후의 gradient가 모두 0이 되는 문제



Softmax Activation Function
Multi-Class Classification에서
output vector의 형태가 총합이 1이고
각각 [0, 1] 사이의 확률분포를 가지는 activation function을 softmax layer 이라 한다
- 소프트맥스(softmax) 함수는 모델의 출력을 확률로 해석할 수 있게 변환해 주는 연산
- 분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측

